平行四边形的判定
图片预览



文档简介
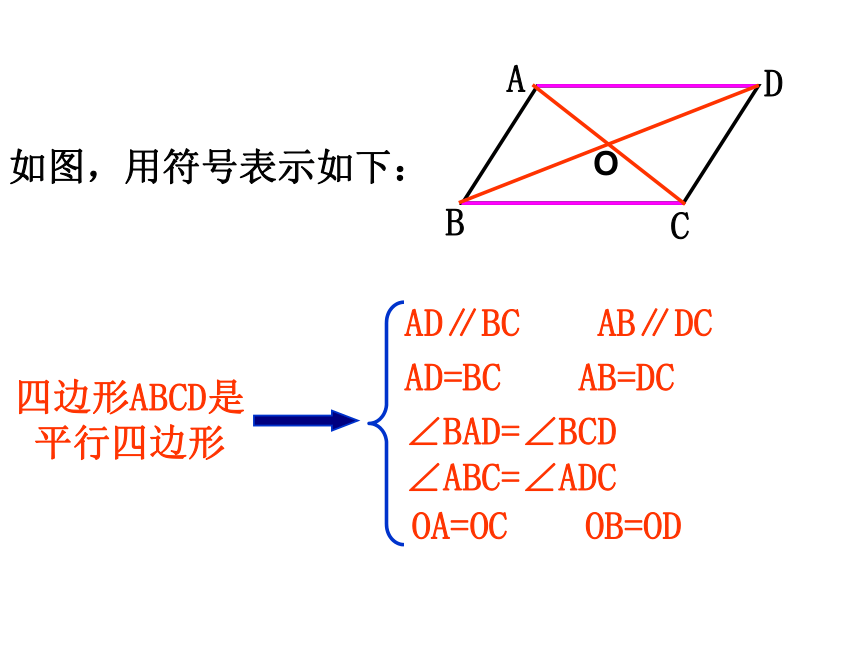
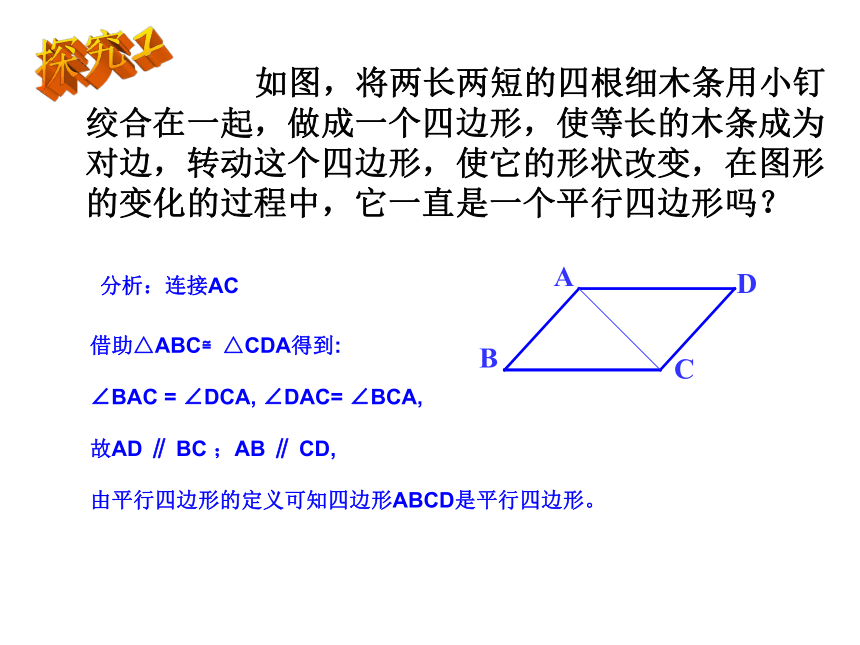
课件19张PPT。叶城县第二中学 陈艳19.1.2平行四边形的判定1温故知新平行四边形的两组对边分别平行且相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分。两组对边分别平行的四边形叫做平行四边形.2、我们学习了平行四边形的哪些性质?1、什么是平行四边形?AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:OA=OC OB=OD思考平行四边形的两组对边分别平行;平行四边形的两组对角分别相等;我们得到的这些逆命题都成立吗?我们一起探讨一下吧:平行四边形的对角线互相平分。思考:我们已经学习了平行四边形的这些性质,那么它们的逆命题各是什么呢?①两组对边分别平行的四边形是平行四边形; ③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形。②两组对边分别相等的四边形是平行四边形;平行四边形的两组对边分别相等;探究1 如图,将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边,转动这个四边形,使它的形状改变,在图形的变化的过程中,它一直是一个平行四边形吗?
借助△ABC≌△CDA得到:
∠BAC = ∠DCA, ∠DAC= ∠BCA,
故AD ∥ BC ;AB ∥ CD,
由平行四边形的定义可知四边形ABCD是平行四边形。分析:连接AC
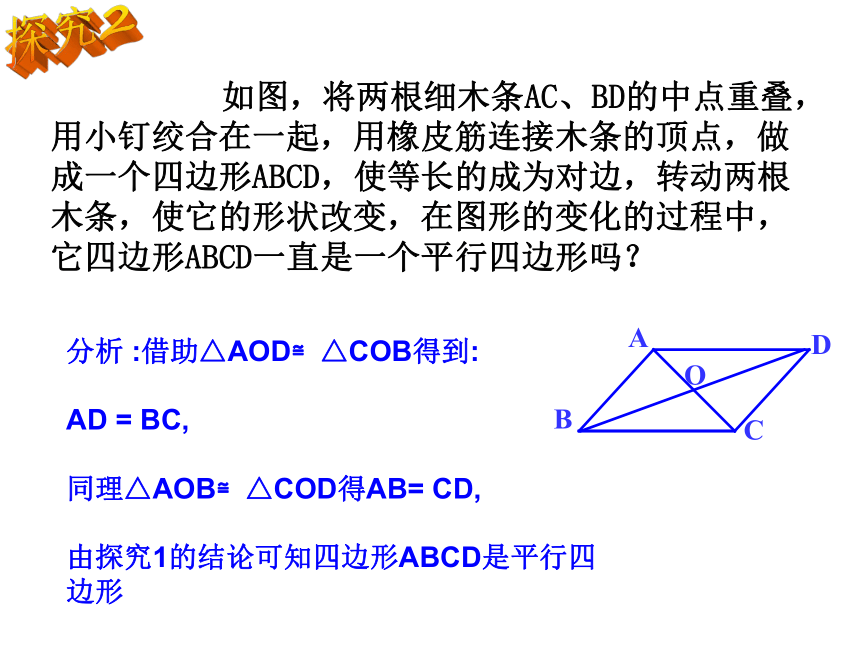
如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,使等长的成为对边,转动两根木条,使它的形状改变,在图形的变化的过程中,它四边形ABCD一直是一个平行四边形吗?分析 :借助△AOD≌△COB得到:
AD = BC,
同理△AOB≌△COD得AB= CD,
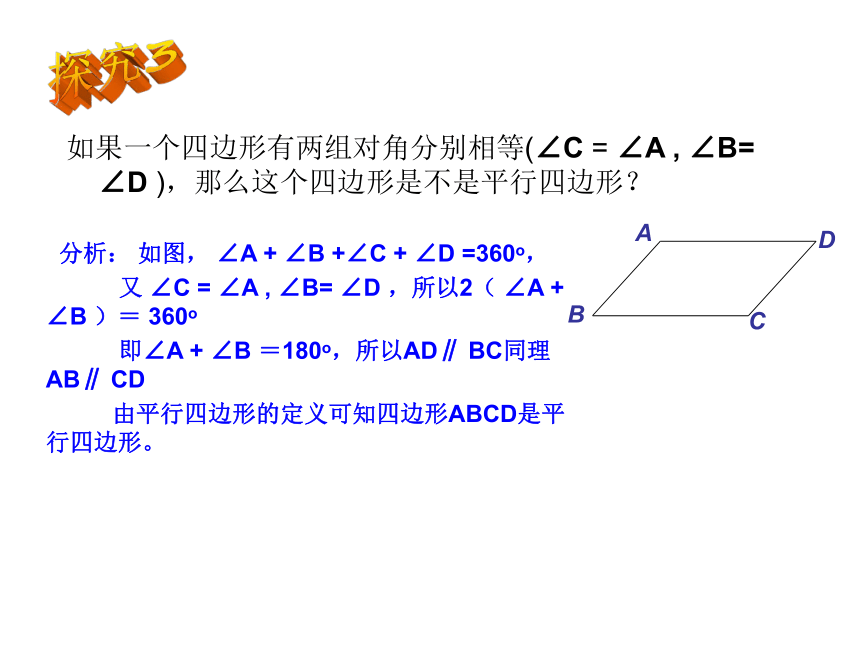
由探究1的结论可知四边形ABCD是平行四边形探究2如果一个四边形有两组对角分别相等(∠C = ∠A , ∠B= ∠D ),那么这个四边形是不是平行四边形? 分析: 如图, ∠A + ∠B +∠C + ∠D =360o,
又 ∠C = ∠A , ∠B= ∠D ,所以2( ∠A + ∠B )= 360o
即∠A + ∠B =180o,所以AD∥ BC同理 AB∥ CD
由平行四边形的定义可知四边形ABCD是平行四边形。
探究3两组对边分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,我们如何证明? 证明:连结AC∴AB∥DC,AD∥BC4123∴∠1=∠2, ∠3=∠4AC=CA(公共边)∴△ABC ≌ △CDA (SSS) AD=BC(已知)AD=BC AB=DC四边形ABCD是平行四边形平行四边形判定定理1 已知:如图,在四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形 .AB=CD(已知)在△ABC 和△CDA中 ∴四边形ABCD是平行四边形用符号表示如下:对角线互相平分的四边形是平行四边形。 已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。同理可证AB=DCOA=OC 平行四边形判定定理2证明:∵四边形ABCD是平行四边形 OA=OC OB=OD用符号表示:想一想平行四边形的这个判定方法,又该如何证明呢? OB=OD ∠AOD=∠COD四边形ABCD是平行四边形∴△AOD ≌ △COB∴AB=DC两组对角分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,又怎么证明呢? 证明:∴AB∥DC,AD∥BC∠A+∠B+∠C+∠D=180°∠A=∠C∠B=∠D 四边形ABCD是平行四边形平行四边形判定定理2推论 已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .在四边形ABCD中 ∴四边形ABCD是平行四边形用符号表示如下:∵∠A=∠C, ∠B=∠D∴∠A+∠D=180°, ∠A+∠B=180°归纳两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形例题分析:首先从结论出发判定平行四边形的
方法有哪些?再根据题目中的已知条件考
虑选用最恰当的判定方法:
对角线互相平分的四边形是平行四边形。由四边形ABCD是平行四边形可知AO=CO,BO=DO,又因为AE=CF,所以AO-AE=CO-CF即EO=FO,而BO=CO.所以四边形ABCD是平行四边形。理由: 证明过程如下:又OB=OD证明:∵ 四边形ABCD是平行四边形∴OA=OC, OB=OD∵AE=CF∴OE=OF例题∴四边形BFDE是平行四边形OB=OD AE=CF OE=OF四边形ABCD是平行四边形OA=OC四边形BFDE是平行四边形你还有其他的证明方法吗?用符号表示如下:练习 1、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:看谁最快2、一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。练习3、一组对边相等,一组对角相等的四边形是平行四边形吗?
不一定。如图4、有两条边相等,并且另外的两条边也相等的四边形一定是平行
四边形吗? 不一定。如右图看谁最快①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题练习看谁最快①②③④1、两组对边分别平行的四边形是平行四边形。2、两组对边分别相等的四边形是平行四边形。3、对角线互相平分的四边形是平行四边形。4、两组对角分别相等的四边形是平行四边形。谈谈你在这节课中,有什么收获?小结平行四边形的判定方法:课后作业必做题(1)课本第100页第5题.
(2) 已知,AD是△ABC的中线,延长AD到E,使DE=AD,连接EB,EC.
求证:四边形ABEC是平行四边形.
(3) 已知平行四边形ABCD中,对角线AC,BD交于点O,EF经过点O,与AB交于点E,与CD交于点F。
求证:四边形AECF是平行四边形.再见
借助△ABC≌△CDA得到:
∠BAC = ∠DCA, ∠DAC= ∠BCA,
故AD ∥ BC ;AB ∥ CD,
由平行四边形的定义可知四边形ABCD是平行四边形。分析:连接AC
如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,使等长的成为对边,转动两根木条,使它的形状改变,在图形的变化的过程中,它四边形ABCD一直是一个平行四边形吗?分析 :借助△AOD≌△COB得到:
AD = BC,
同理△AOB≌△COD得AB= CD,
由探究1的结论可知四边形ABCD是平行四边形探究2如果一个四边形有两组对角分别相等(∠C = ∠A , ∠B= ∠D ),那么这个四边形是不是平行四边形? 分析: 如图, ∠A + ∠B +∠C + ∠D =360o,
又 ∠C = ∠A , ∠B= ∠D ,所以2( ∠A + ∠B )= 360o
即∠A + ∠B =180o,所以AD∥ BC同理 AB∥ CD
由平行四边形的定义可知四边形ABCD是平行四边形。
探究3两组对边分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,我们如何证明? 证明:连结AC∴AB∥DC,AD∥BC4123∴∠1=∠2, ∠3=∠4AC=CA(公共边)∴△ABC ≌ △CDA (SSS) AD=BC(已知)AD=BC AB=DC四边形ABCD是平行四边形平行四边形判定定理1 已知:如图,在四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形 .AB=CD(已知)在△ABC 和△CDA中 ∴四边形ABCD是平行四边形用符号表示如下:对角线互相平分的四边形是平行四边形。 已知,如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD,求证:四边形ABCD是平行四边形。同理可证AB=DCOA=OC 平行四边形判定定理2证明:∵四边形ABCD是平行四边形 OA=OC OB=OD用符号表示:想一想平行四边形的这个判定方法,又该如何证明呢? OB=OD ∠AOD=∠COD四边形ABCD是平行四边形∴△AOD ≌ △COB∴AB=DC两组对角分别相等的四边形是平行四边形.想一想平行四边形这个判定方法,又怎么证明呢? 证明:∴AB∥DC,AD∥BC∠A+∠B+∠C+∠D=180°∠A=∠C∠B=∠D 四边形ABCD是平行四边形平行四边形判定定理2推论 已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .在四边形ABCD中 ∴四边形ABCD是平行四边形用符号表示如下:∵∠A=∠C, ∠B=∠D∴∠A+∠D=180°, ∠A+∠B=180°归纳两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形例题分析:首先从结论出发判定平行四边形的
方法有哪些?再根据题目中的已知条件考
虑选用最恰当的判定方法:
对角线互相平分的四边形是平行四边形。由四边形ABCD是平行四边形可知AO=CO,BO=DO,又因为AE=CF,所以AO-AE=CO-CF即EO=FO,而BO=CO.所以四边形ABCD是平行四边形。理由: 证明过程如下:又OB=OD证明:∵ 四边形ABCD是平行四边形∴OA=OC, OB=OD∵AE=CF∴OE=OF例题∴四边形BFDE是平行四边形OB=OD AE=CF OE=OF四边形ABCD是平行四边形OA=OC四边形BFDE是平行四边形你还有其他的证明方法吗?用符号表示如下:练习 1、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:看谁最快2、一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。练习3、一组对边相等,一组对角相等的四边形是平行四边形吗?
不一定。如图4、有两条边相等,并且另外的两条边也相等的四边形一定是平行
四边形吗? 不一定。如右图看谁最快①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题练习看谁最快①②③④1、两组对边分别平行的四边形是平行四边形。2、两组对边分别相等的四边形是平行四边形。3、对角线互相平分的四边形是平行四边形。4、两组对角分别相等的四边形是平行四边形。谈谈你在这节课中,有什么收获?小结平行四边形的判定方法:课后作业必做题(1)课本第100页第5题.
(2) 已知,AD是△ABC的中线,延长AD到E,使DE=AD,连接EB,EC.
求证:四边形ABEC是平行四边形.
(3) 已知平行四边形ABCD中,对角线AC,BD交于点O,EF经过点O,与AB交于点E,与CD交于点F。
求证:四边形AECF是平行四边形.再见
