第22章相似形单元复习题(含解析) 2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 第22章相似形单元复习题(含解析) 2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 20:58:05 | ||
图片预览




文档简介
沪科版九年级数学上册22章相似性单元复习题
一、选择题
1.下列各组图形中,一定是相似图形的是( )
A.两个等腰梯形 B.两个矩形
C.两个直角三角形 D.两个等边三角形
2.如图,下列条件不能判定△ABC与△ADE相似的是( )
A. B.∠B=∠ADE C. D.∠C=∠AED
3.已知△ABC∽△A'B'C' ,BC=3,B'C'=1.8,则△ABC与△A'B'C'的相似比为( ).
A.2:3 B.3:2 C.5:3 D.3:5
4.如图,五边形与五边形是位似图形,O为位似中心,,则为( )
A.2:3 B.3:2 C.1:2 D.2:1
5.若上,且3a-2b+c=3,则2a+4b-3c的值是( ).
A.14 B.42 C.7 D.
6.如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④,能满足与相似的条件以及性质的是( )
A.①②④ B.①③④ C.②③④ D.①②③
7.下列判断中,正确的是( )
A.各有一个角是的两个等腰三角形相似
B.邻边之比为2:1的两个等腰三角形相似
C.各有一个角是的两个等腰三角形相似
D.邻边之比为2:3的两个等腰三角形相似
8.如图,在Rt△ABC中,∠A= Rt∠,AB=3,AC=4.P是BC边上一点,作PE⊥AB于点E,PD⊥AC于点D.设BP=x,则PD+PE=( ).
A.+3 B.4-
C. D.
9.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC.若S△BDC:S△ADC=1:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
10.一个面积为的四边形,它的位似图形为四边形,位似中心为,若,则四边形的面积为( )
A. B.
C.或 D.以上都不对
二、填空题
11.若两个相似多边形的相似比是2:3,则它们的周长比是 .
12.如图,D是ΔABC边AB延长线上一点,请添加一个条件 ,使ΔACD∽ΔABC.
13.如图,平面直角坐标系中,正方形和正方形是以O为位似中心的位似图形,位似比为1:2,点F,B,C在x轴上,若,则点G的坐标为 .
14.如图,在 中,在上,、交于,若::,则: .
三、解答题
15.已知.
判断是否成立,并说明理由.
16.如图,点D为边上一点,连接,,,.
求证:.
17.已知,延长到,使取的中点,连接交于点.
(1)求的值;
(2)若,,求的长.
18.如图,已知 是坐标原点, 、 的坐标分别为 , .
(1)在 轴的左侧以 为位似中心作 的位似 ,使新图与原图的相似比为 ;
(2)分别写出 、 的对应点 、 的坐标.
四、综合题
19.如图,已知,与相交于点E,点F在线段上,,.
(1)求证:;
(2)求.
20.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
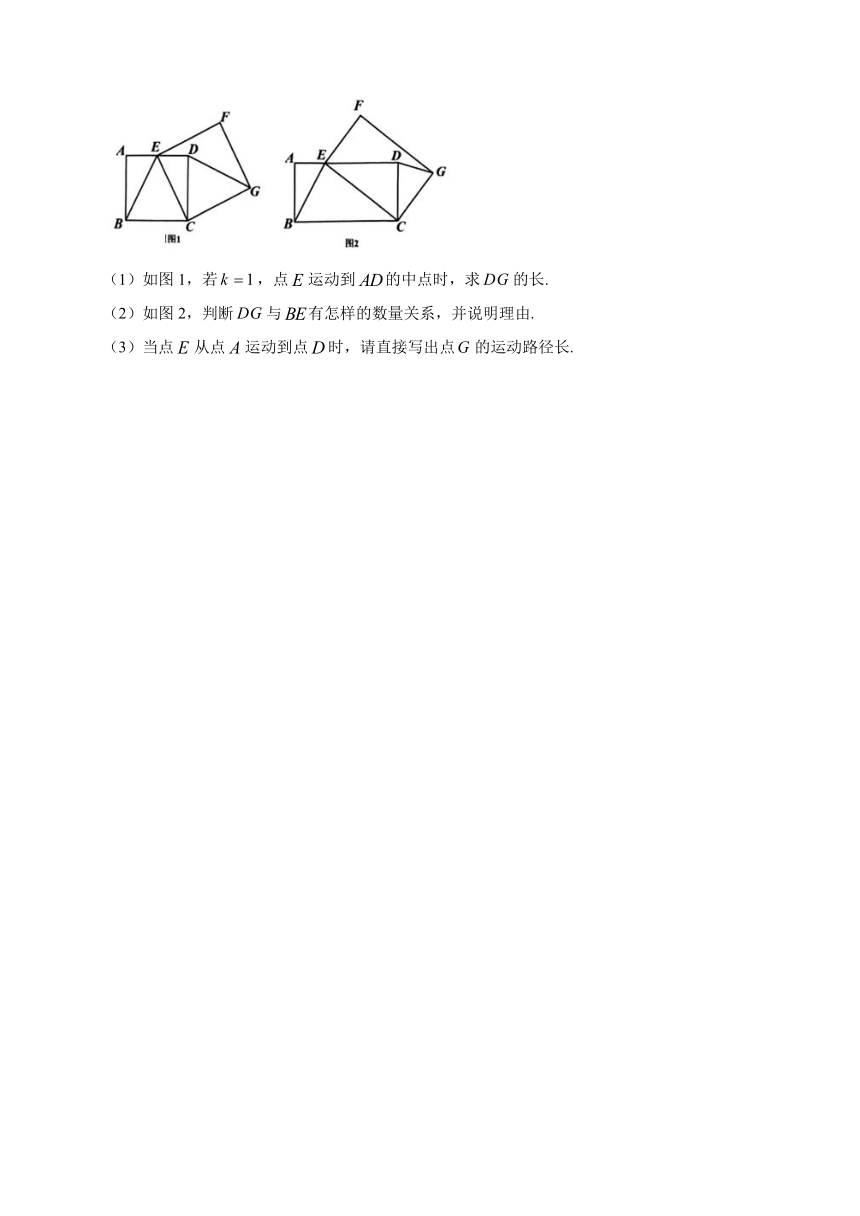
21.已知在矩形中,,,点是边上的一个动点,以为边,在的右侧作矩形,且,连接,.
(1)如图1,若,点运动到的中点时,求的长.
(2)如图2,判断与有怎样的数量关系,并说明理由.
(3)当点从点运动到点时,请直接写出点的运动路径长.
答案解析部分
1.【答案】D
2.【答案】C
【解析】【解答】解:∵∠EAD=∠BAC,
当,∠A=∠A,
∴△ABC∽△ADE,故选项A不符合题意;
当∠B=∠ADE时,△ABC∽△ADE,故选项B不符合题意;
C选项中∠A不是成比例的两边的夹角,故选项C符合题意;
当∠C=∠AED时,△ABC∽△ADE,故选项D不符合题意.
故答案为:C.
【分析】由于两个三角形具有公共角∠EAD=∠BAC,故可以添加∠B=∠ADE或∠C=∠AED,利用有两组角对应相等的两个三角形相似即可判断出△ABC∽△ADE;也可以添加,利用有两组边成比例,且夹角相等的两个三角形相似可判断△ABC∽△ADE,从而一一判断得出答案.
3.【答案】C
4.【答案】D
【解析】【解答】解:五边形ABCDE与五边形A'B'C'D'E'是位似图形
即
故答案为:D.
【分析】根据位似图形的位似比等于对应点到位似中心的距离之比可得答案.
5.【答案】D
6.【答案】D
【解析】【解答】解:A、∵,,
∴,
∴,
∴,不符合题意;
B、∵,
∴,
∵,
∴,
∴,
∴,
∴,不符合题意;
C、∵,
∴,
∵,
∴,
∴,
∴,
∴,不符合题意;
D、∵,,
∴,
∴,
∴,符合题意;
故答案为:D.
【分析】利用相似三角形的判定方法和性质逐项判断即可。
7.【答案】B
【解析】【解答】A.没有明确指出角是顶角还是底角无法判定,故A选项不符合题意.
B.因为比值为2:1,所以大边一定是腰,所以对边成比例,相似,故B选项符合题意.
C.没有明确指出角是顶角还是底角无法判定,故C选项不符合题意.
D.没有指明谁是底边谁是腰,无法判定,故A选项不符合题意.
故答案为:A.
【分析】利用相似三角形的判定方法逐项判断即可。
8.【答案】A
9.【答案】D
【解析】【解答】解:∵,
∴BD∶AD=1∶3,
∴BD∶AB=1∶4
∵,
∴△BDE∽△BAC,
∴
∵DE∥AC,
∴△DEO∽△CAO,
∴S△DEO∶S△CAO=.
故答案为:D.
【分析】由同高三角形的面积之比就等于底之比可得BD∶AD=1∶3,则BD∶AB=1∶4,由平行于三角形一边的直线截其它两边,所截三角形与原三角形相似得△BDE∽△BAC,由相似三角形对应边成比例得进而根据平行于三角形一边的直线,解其它两边的延长线,所截三角形与原三角形相似得△DEO∽△CAO,进而根据相似三角形的面积之比等于底之比可得结论.
10.【答案】C
【解析】【解答】解:由题可知四边形的相似比为1:1或1:3,
四边形的面积之比等于相似比的平方,且四边形的面积为,
四边形 的面积为或.
故答案为:C.
【分析】利用位似图形的性质:相似图形的面积之比等于相似比的平方求解即可。
11.【答案】2:3
【解析】【解答】解:∵ 两个相似多边形的相似比是2:3 ,
∴这两个相似多边形的周长之比是2∶3.
故答案为:2∶3.
【分析】根据相似多边形周长的比等于相似比即可直接得出答案.
12.【答案】AC=AB AD(答案不唯一)
【解析】【解答】解:添加:AC=AB AD
∵AC=AB AD
∴
∵∠A=∠A
∴ΔACD∽ΔABC.
故答案为:AC=AB AD(答案不唯一).
【分析】先求出,再利用相似三角形的判定方法证明即可。
13.【答案】(6,3)
【解析】【解答】解:∵正方形和正方形是以O为位似中心的位似图形,位似比为1:2,
∴,,,
∴,
∴,即,
解得:,,
∴点G的坐标为,
故答案为:.
【分析】根据正方形的性质以及位似图形的性质可得BC=AD=CD=6,BG∥CD,,证明△OBG∽△OCD,根据相似三角形的性质可得OB、BG的值,进而可得点G的坐标.
14.【答案】:
15.【答案】解:比例式成立. 理由如下:
∵ ,∴ ,
∴1- =1- ,
即
【解析】【分析】利用比例的性质可得到,可得到,再将等式的两边通分即可证得结论.
16.【答案】证明:∵,,
∴,
∴,,即,
又∵,
∴
【解析】【分析】由线段的和差关系可得AB=AD+BD=8,根据已知条件可得,然后根据相似三角形的判定定理进行证明.
17.【答案】(1)解:如图,连接、.
点是的中点,,
是的中位线,
,
∽,
,
;
(2)解:点是的中点,,,
.
由知,,则,故AE,
.
18.【答案】(1)解:如图所示:
(2)解:如图所示: ,
【解析】【分析】(1)分别延长AO和BO使得DO=2AO,CO=2BO,连接CD即可得出所得图形。
(2)根据(1)中所做的位似图形,将C和D的坐标写出即可。
19.【答案】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴.
【解析】【分析】(1)由平行线分线段成比例可得到,结合可得, 利用平行线分线段可证结论;
(2)由平行线分线段成比例可得,,继而得解.
20.【答案】(1)解:∵D、E分别是边AB、AC的中点,
∴ ,DE BC,
又BC=8,
∴DE=4,
∵DE BC,
∴∠AED=∠C,
∵∠F=∠C,
∴∠AED=∠F,
∴DF=DE=4.
(2)证明:∵AB=AC,
∴∠B=∠C,
∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
【解析】【分析】(1)易得DE是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半,可得DE=4,DE∥BC,根据二直线平行,同位角相等得∠AED=∠C,结合已知得∠AED=∠F,最后根据等角对等边可得FD的长;
(2)由据等边对等角得∠B=∠C,由平行线的性质得 ∠AED=∠C,∠ADE=∠B 由(1)知 ∠AED=∠F, 故∠ADE=∠F, 从而根据有两组角对应相等的两个三角形相似得出结论.
21.【答案】(1)解:矩形中,,,,
∴,则矩形是正方形,
∵点到的中点,
∴,,
在中,,
∴矩形,,
∵,,
∴,
在,中,
∴,
∴,
∵,
∴.
(2)解:,理由如下,
矩形,,,矩形,,
∴,
∴,,即,
∵,,
∴,
∴,
∴.
(3)解:点的运动路径长是2
【解析】【解答】(3)解:点从点运动到点,如图所示,
过点作的延长线于点,的延长线交延长线于点,
∵,
∴,,
∴,
∴,且,
∴,
∵,,
∴,
∴点在定直线上运动,
∴当点与点重合时,,,此时点与点重合;
当点与点重合时,,,点与点重合,
∴点的运动路径长是2.
【分析】(1)由题意可得矩形ABCD为正方形,由中点的概念可得AE=DE=1,BE=CE,利用勾股定理可得CE的值,根据矩形的性质可得CE=CCG,由同角的余角相等可得∠BCE=∠DCG,利用SAS证明△BEC≌△DGC,得到DG=BE,据此求解;
(2)由题意可得AD=BC=2k,证明△BEC∽△DGC,然后根据相似三角形的性质进行解答;
(3)过点G作GM⊥BC的延长线于点M,MG的延长线交AD延长线于点H,证明△ECD∽△CGM,根据相似三角形的性质可得CM,推出点G在定直线GM上运动,当点E与点A重合时,ED=AD,GM=2,此时点G与点H重合;当点E与点D重合时,ED=0,GM=0,点G与点M重合,据此解答.
一、选择题
1.下列各组图形中,一定是相似图形的是( )
A.两个等腰梯形 B.两个矩形
C.两个直角三角形 D.两个等边三角形
2.如图,下列条件不能判定△ABC与△ADE相似的是( )
A. B.∠B=∠ADE C. D.∠C=∠AED
3.已知△ABC∽△A'B'C' ,BC=3,B'C'=1.8,则△ABC与△A'B'C'的相似比为( ).
A.2:3 B.3:2 C.5:3 D.3:5
4.如图,五边形与五边形是位似图形,O为位似中心,,则为( )
A.2:3 B.3:2 C.1:2 D.2:1
5.若上,且3a-2b+c=3,则2a+4b-3c的值是( ).
A.14 B.42 C.7 D.
6.如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④,能满足与相似的条件以及性质的是( )
A.①②④ B.①③④ C.②③④ D.①②③
7.下列判断中,正确的是( )
A.各有一个角是的两个等腰三角形相似
B.邻边之比为2:1的两个等腰三角形相似
C.各有一个角是的两个等腰三角形相似
D.邻边之比为2:3的两个等腰三角形相似
8.如图,在Rt△ABC中,∠A= Rt∠,AB=3,AC=4.P是BC边上一点,作PE⊥AB于点E,PD⊥AC于点D.设BP=x,则PD+PE=( ).
A.+3 B.4-
C. D.
9.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC.若S△BDC:S△ADC=1:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
10.一个面积为的四边形,它的位似图形为四边形,位似中心为,若,则四边形的面积为( )
A. B.
C.或 D.以上都不对
二、填空题
11.若两个相似多边形的相似比是2:3,则它们的周长比是 .
12.如图,D是ΔABC边AB延长线上一点,请添加一个条件 ,使ΔACD∽ΔABC.
13.如图,平面直角坐标系中,正方形和正方形是以O为位似中心的位似图形,位似比为1:2,点F,B,C在x轴上,若,则点G的坐标为 .
14.如图,在 中,在上,、交于,若::,则: .
三、解答题
15.已知.
判断是否成立,并说明理由.
16.如图,点D为边上一点,连接,,,.
求证:.
17.已知,延长到,使取的中点,连接交于点.
(1)求的值;
(2)若,,求的长.
18.如图,已知 是坐标原点, 、 的坐标分别为 , .
(1)在 轴的左侧以 为位似中心作 的位似 ,使新图与原图的相似比为 ;
(2)分别写出 、 的对应点 、 的坐标.
四、综合题
19.如图,已知,与相交于点E,点F在线段上,,.
(1)求证:;
(2)求.
20.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
21.已知在矩形中,,,点是边上的一个动点,以为边,在的右侧作矩形,且,连接,.
(1)如图1,若,点运动到的中点时,求的长.
(2)如图2,判断与有怎样的数量关系,并说明理由.
(3)当点从点运动到点时,请直接写出点的运动路径长.
答案解析部分
1.【答案】D
2.【答案】C
【解析】【解答】解:∵∠EAD=∠BAC,
当,∠A=∠A,
∴△ABC∽△ADE,故选项A不符合题意;
当∠B=∠ADE时,△ABC∽△ADE,故选项B不符合题意;
C选项中∠A不是成比例的两边的夹角,故选项C符合题意;
当∠C=∠AED时,△ABC∽△ADE,故选项D不符合题意.
故答案为:C.
【分析】由于两个三角形具有公共角∠EAD=∠BAC,故可以添加∠B=∠ADE或∠C=∠AED,利用有两组角对应相等的两个三角形相似即可判断出△ABC∽△ADE;也可以添加,利用有两组边成比例,且夹角相等的两个三角形相似可判断△ABC∽△ADE,从而一一判断得出答案.
3.【答案】C
4.【答案】D
【解析】【解答】解:五边形ABCDE与五边形A'B'C'D'E'是位似图形
即
故答案为:D.
【分析】根据位似图形的位似比等于对应点到位似中心的距离之比可得答案.
5.【答案】D
6.【答案】D
【解析】【解答】解:A、∵,,
∴,
∴,
∴,不符合题意;
B、∵,
∴,
∵,
∴,
∴,
∴,
∴,不符合题意;
C、∵,
∴,
∵,
∴,
∴,
∴,
∴,不符合题意;
D、∵,,
∴,
∴,
∴,符合题意;
故答案为:D.
【分析】利用相似三角形的判定方法和性质逐项判断即可。
7.【答案】B
【解析】【解答】A.没有明确指出角是顶角还是底角无法判定,故A选项不符合题意.
B.因为比值为2:1,所以大边一定是腰,所以对边成比例,相似,故B选项符合题意.
C.没有明确指出角是顶角还是底角无法判定,故C选项不符合题意.
D.没有指明谁是底边谁是腰,无法判定,故A选项不符合题意.
故答案为:A.
【分析】利用相似三角形的判定方法逐项判断即可。
8.【答案】A
9.【答案】D
【解析】【解答】解:∵,
∴BD∶AD=1∶3,
∴BD∶AB=1∶4
∵,
∴△BDE∽△BAC,
∴
∵DE∥AC,
∴△DEO∽△CAO,
∴S△DEO∶S△CAO=.
故答案为:D.
【分析】由同高三角形的面积之比就等于底之比可得BD∶AD=1∶3,则BD∶AB=1∶4,由平行于三角形一边的直线截其它两边,所截三角形与原三角形相似得△BDE∽△BAC,由相似三角形对应边成比例得进而根据平行于三角形一边的直线,解其它两边的延长线,所截三角形与原三角形相似得△DEO∽△CAO,进而根据相似三角形的面积之比等于底之比可得结论.
10.【答案】C
【解析】【解答】解:由题可知四边形的相似比为1:1或1:3,
四边形的面积之比等于相似比的平方,且四边形的面积为,
四边形 的面积为或.
故答案为:C.
【分析】利用位似图形的性质:相似图形的面积之比等于相似比的平方求解即可。
11.【答案】2:3
【解析】【解答】解:∵ 两个相似多边形的相似比是2:3 ,
∴这两个相似多边形的周长之比是2∶3.
故答案为:2∶3.
【分析】根据相似多边形周长的比等于相似比即可直接得出答案.
12.【答案】AC=AB AD(答案不唯一)
【解析】【解答】解:添加:AC=AB AD
∵AC=AB AD
∴
∵∠A=∠A
∴ΔACD∽ΔABC.
故答案为:AC=AB AD(答案不唯一).
【分析】先求出,再利用相似三角形的判定方法证明即可。
13.【答案】(6,3)
【解析】【解答】解:∵正方形和正方形是以O为位似中心的位似图形,位似比为1:2,
∴,,,
∴,
∴,即,
解得:,,
∴点G的坐标为,
故答案为:.
【分析】根据正方形的性质以及位似图形的性质可得BC=AD=CD=6,BG∥CD,,证明△OBG∽△OCD,根据相似三角形的性质可得OB、BG的值,进而可得点G的坐标.
14.【答案】:
15.【答案】解:比例式成立. 理由如下:
∵ ,∴ ,
∴1- =1- ,
即
【解析】【分析】利用比例的性质可得到,可得到,再将等式的两边通分即可证得结论.
16.【答案】证明:∵,,
∴,
∴,,即,
又∵,
∴
【解析】【分析】由线段的和差关系可得AB=AD+BD=8,根据已知条件可得,然后根据相似三角形的判定定理进行证明.
17.【答案】(1)解:如图,连接、.
点是的中点,,
是的中位线,
,
∽,
,
;
(2)解:点是的中点,,,
.
由知,,则,故AE,
.
18.【答案】(1)解:如图所示:
(2)解:如图所示: ,
【解析】【分析】(1)分别延长AO和BO使得DO=2AO,CO=2BO,连接CD即可得出所得图形。
(2)根据(1)中所做的位似图形,将C和D的坐标写出即可。
19.【答案】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴.
【解析】【分析】(1)由平行线分线段成比例可得到,结合可得, 利用平行线分线段可证结论;
(2)由平行线分线段成比例可得,,继而得解.
20.【答案】(1)解:∵D、E分别是边AB、AC的中点,
∴ ,DE BC,
又BC=8,
∴DE=4,
∵DE BC,
∴∠AED=∠C,
∵∠F=∠C,
∴∠AED=∠F,
∴DF=DE=4.
(2)证明:∵AB=AC,
∴∠B=∠C,
∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
【解析】【分析】(1)易得DE是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半,可得DE=4,DE∥BC,根据二直线平行,同位角相等得∠AED=∠C,结合已知得∠AED=∠F,最后根据等角对等边可得FD的长;
(2)由据等边对等角得∠B=∠C,由平行线的性质得 ∠AED=∠C,∠ADE=∠B 由(1)知 ∠AED=∠F, 故∠ADE=∠F, 从而根据有两组角对应相等的两个三角形相似得出结论.
21.【答案】(1)解:矩形中,,,,
∴,则矩形是正方形,
∵点到的中点,
∴,,
在中,,
∴矩形,,
∵,,
∴,
在,中,
∴,
∴,
∵,
∴.
(2)解:,理由如下,
矩形,,,矩形,,
∴,
∴,,即,
∵,,
∴,
∴,
∴.
(3)解:点的运动路径长是2
【解析】【解答】(3)解:点从点运动到点,如图所示,
过点作的延长线于点,的延长线交延长线于点,
∵,
∴,,
∴,
∴,且,
∴,
∵,,
∴,
∴点在定直线上运动,
∴当点与点重合时,,,此时点与点重合;
当点与点重合时,,,点与点重合,
∴点的运动路径长是2.
【分析】(1)由题意可得矩形ABCD为正方形,由中点的概念可得AE=DE=1,BE=CE,利用勾股定理可得CE的值,根据矩形的性质可得CE=CCG,由同角的余角相等可得∠BCE=∠DCG,利用SAS证明△BEC≌△DGC,得到DG=BE,据此求解;
(2)由题意可得AD=BC=2k,证明△BEC∽△DGC,然后根据相似三角形的性质进行解答;
(3)过点G作GM⊥BC的延长线于点M,MG的延长线交AD延长线于点H,证明△ECD∽△CGM,根据相似三角形的性质可得CM,推出点G在定直线GM上运动,当点E与点A重合时,ED=AD,GM=2,此时点G与点H重合;当点E与点D重合时,ED=0,GM=0,点G与点M重合,据此解答.
