2023—2024学年沪科版八年级数学上册第13章三角形中的边角关系 命题与证明单元复习题(含解析)
文档属性
| 名称 | 2023—2024学年沪科版八年级数学上册第13章三角形中的边角关系 命题与证明单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 21:03:09 | ||
图片预览




文档简介
沪科版八年级数学上册第13章三角形中的边角关系 命题与证明单元复习题
一、选择题
1.下列每组数分别表示三条线段长度,将它们首尾顺次相接能构成三角形的是( )
A.,, B.,, C.,, D.,,
2.如图,中AD为中线,,则与的周长之差为( )
A.1 B.2 C.3 D.4
3.三个内角的度数之比为3:4:5,那么是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
4.下列是命题的是( )
A.作两条相交直线 B.∠α和∠β相等吗?
C.全等三角形的对应边相等 D.若,求a的值
5.下列结论正确的是( )
A.有理数与数轴上的点一一对应 B.二次根式有意义条件是
C.立方根等于它本身是 D.如果,那么
6. 如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF,△BEF 的面积分别为 S△ABC,S△ADF,S△BEF,且 S△ABC=18,则 S△ADF﹣S△BEF( )
A.5 B.4 C.3 D.2
7.等腰三角形的一个角是,则它的底角是( )
A. B. C.或 D.或
8.如图,是的平分线,,,则( )
A. B. C. D.
9.下列命题的逆命题是真命题的是( )
A.两直线平行,内错角相等 B.如果,那么
C.钝角三角形中有两个锐角 D.对顶角相等
10.下列说法正确的个数是( )
①函数的图象不经过第三象限
②一组数据5,6,7,6,8,10的众数和中位数都是6
③将的图象沿y轴向下平移3个单位长度后,图象经过原点
④式子有意义的条件是且
A.1 B.2 C.3 D.4
二、填空题
11. 如图,是的一条中线,若,则 .
12.将命题“对顶角相等”用“如果…那么…”的形式可以改写为 .
13.如图,在中,点D、E、F分别是线段BC、AD、CE的中点,且,则 .
14.下列命题:①内错角相等;②平方根等于本身的数是0;③已知点A(2,3),B(2,﹣3),则直线AB∥y轴:④不等式组1<x<a的整数解只有1个,则a的取值范围为2<a≤3;其中是真命题的有: (填序号).
三、解答题
15. 如图,中,于点E,AF是的平分线,交BE于点F,,,求的度数.
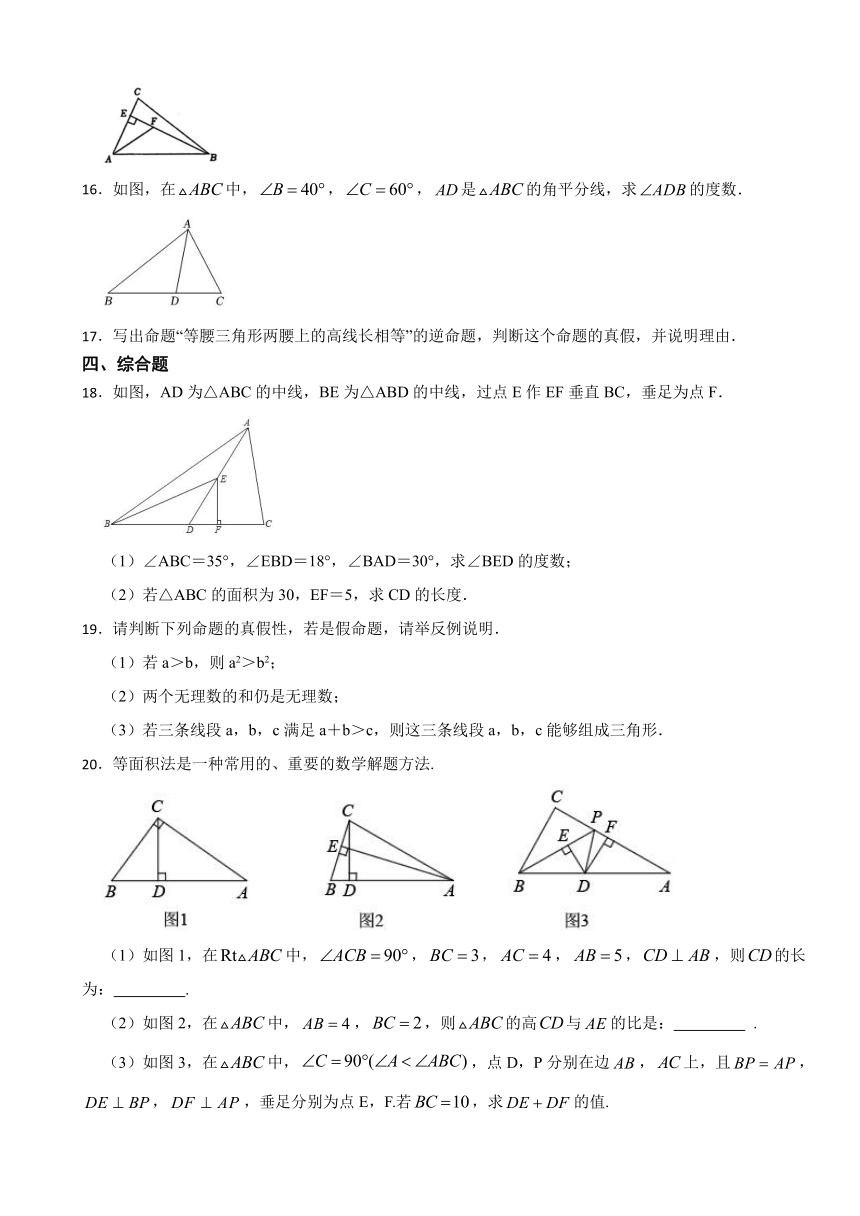
16.如图,在中,,,是的角平分线,求的度数.
17.写出命题“等腰三角形两腰上的高线长相等”的逆命题,判断这个命题的真假,并说明理由.
四、综合题
18.如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABC=35°,∠EBD=18°,∠BAD=30°,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD的长度.
19.请判断下列命题的真假性,若是假命题,请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
20.等面积法是一种常用的、重要的数学解题方法.
(1)如图1,在中,,,,,,则的长为: .
(2)如图2,在中,,,则的高与的比是: .
(3)如图3,在中,,点D,P分别在边,上,且,,,垂足分别为点E,F.若,求的值.
答案解析部分
1.【答案】D
【解析】【解答】解:A:1+2<6,不能构成三角形,不符合题意;
B:2+2=4,不能构成三角形,不符合题意;
C:1+2=3,不能构成三角形,不符合题意;
D:2+3>4,能构成三角形,符合题意.
故答案为:D
【分析】根据三角形三边关系即可求出答案.
2.【答案】B
【解析】【解答】解:∵AD为△ABC的中线,
∴BD=DC,
∴=(AB+AD+BD)-(AC+AD+DC)=AB﹣AC=8﹣6=2,
故答案为:B.
【分析】根据三角形的中线的定义得到BD=DC,然后根据三角形的周长公式表示出两三角形的周长之差计算即可.
3.【答案】B
【解析】【解答】解:设这三个内角的度数分别为3x°,4x°,5x°.
则3x+4x+5x=180,
解得x=15,
∴5x°=75°,3x°=45°,4x°=60°,
所以这个三角形是锐角三角形,
故答案为:B.
【分析】已知三角形三个内角的度数之比,可以设这三个内角的度数分别为3x°,4x°,5x°,根据三角形的内角和等于180°列方程求解即可求出三个内角的度数,再从角的角度来判断三角形的形状.
4.【答案】C
【解析】【解答】解:A、“作两条相交直线”,它不是命题,所以A选项错误;
B、“∠α和∠β相等吗?”,它不是命题,所以A选项错误;
C、全等三角形对应边相等,它是命题,所以C选项正确;
D、“若a2=4,求a的值”,它不是命题,所以D选项错误.
故答案为:D.
【分析】根据命题的定义即:判断一件事情的语句叫做命题,逐个判断即可.
5.【答案】D
【解析】【解答】解:A.实数与数轴上的点一一对应,不符合题意;
B.二次根式有意义条件是全体实数,不符合题意;
C.立方根等于它本身是和0,不符合题意;
D.如果,那么,符合题意.
故答案为:D.
【分析】根据真命题的定义逐项判断即可。
6.【答案】C
7.【答案】D
【解析】【解答】解:当80°的角为顶角时,
底角=(180°-80°)=50°.
情况二:当80°的角为底角时,
80°2=160°,小于180°同样满足
它的底角是或
故答案为:D.
【分析】本题考察了等腰三角形的内角和,底角的知识点。
8.【答案】C
【解析】【解答】∵∠DAE=60°,
∴∠BAD=120°,
∵AD是∠CAE的平分线,
∴∠CAD=∠BAD=60°,
∴∠BAC=180°-∠CAE=180°-120°=60°,
∵∠B=35°,
∴∠D=180°-(∠BAC+∠CAD)-∠B=180°-120°-35°=25°,
∴∠ACB=∠CAD+∠D=60°+25°=85°,
故答案为:C.
【分析】先利用角平分线的定义求出∠CAD=∠BAD=60°,再利用角的运算求出∠D的度数,最后求出∠ACB的度数即可.
9.【答案】A
10.【答案】B
【解析】【解答】解:①∵,∴函数的图象经过一、二、四象限,不过第三象限,原说法符合题意;
②一组数据5,6,7,6,8,10重新排列后为5,6,6,7,8,10,众数是6,中位数是,原说法不符合题意;
③将的图象沿y轴向下平移3个单位长度后的解析式是:,图象不经过原点,原说法不符合题意;
④式子有意义的条件是且,原说法符合题意.
说法正确的有①④,共2个.
故答案为:B.
【分析】根据真命题的定义逐项判断即可。
11.【答案】10
【解析】【解答】解:∵是的一条中线,,
∴BC=2BD=10,
故答案为:10.
【分析】根据三角形的中线求出BC=2BD=10,即可作答。
12.【答案】如果两个角是对顶角,那么这两个角相等
【解析】【解答】解:命题“对顶角相等”用“如果…那么…”的形式可以改写为:如果两个角是对顶角,那么这两个角相等 ;
故答案为: 如果两个角是对顶角,那么这两个角相等 .
【分析】先找出命题的题设和结论,再写成“如果…那么…”的形式即可.
13.【答案】4
【解析】【解答】∵F为CE中点,
∴,
∵E为AD中点,
∴,
∴,
∵F为CE中点,
∴
故答案为:4.
【分析】由中点可以得到三角形的中线,可得到等底等高的三角形的面积相等,用△ABC的面积表示出△BDE和△CDE的面积,从而得到△BCE的面积,再由BF是△BEC的中线可得到△BEF的面积是△ABC的面积的一半,然后代入数据进行计算即可得解.
14.【答案】②③④
【解析】【解答】解:①两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
②平方根等于本身的数是0,正确,是真命题,符合题意;
③已知点A(2,3),B(2,﹣3),则直线AB∥y轴,正确,是真命题,符合题意;
④不等式组1<x<a的整数解只有1个,则a的取值范围为2<a≤3,正确,是真命题,符合题意.
故答案为:②③④.
【分析】根据平行线的性质“两直线平行,内错角相等”可判断①;根据平方根的性质“一个正数有两个平方根,这两个平方根互为相反数,负数没有平方根,0的平方根是0”可判断②;平行于y轴的直线上的点的横坐标相同,据此判断③;根据不等式组的整数解可得a的范围,据此判断④.
15.【答案】解:∵,,
∴.
∵AF是的平分线,
∴.
∵,
∴,
∴.
16.【答案】解:在中,
,,
,
是的角平分线,
,
【解析】【分析】从问题入手,要求的度数,根据三角形的外角和等于不相邻的两个内角和,就需要先求,由此要求,是三角形ABC的一个内角,其他2个内角已知,根据内角和是180°的性质可求,至此整理思路即可。
17.【答案】解:命题“等腰三角形两腰上的高线长相等”的逆命题是两边上的高相等的三角形为等腰三角形,此逆命题为真命题.
如图,在△ABC中,CD⊥AB,BE⊥AC,且CD=BE,
∵BC=BC,
∴△CBD≌△BCE(HL),
∴∠DBC=∠ECB,
∴△ABC为等腰三角形.
【解析】【分析】根据命题与逆命题的性质判断即可.
18.【答案】(1)解:∵∠ABC=35°,∠EBD=18°,
∴∠ABE=35°﹣18°=17°,
∴∠BED=∠ABE+∠BAD=17°+30°=47°
(2)解:∵AD是△ABC的中线,
∴S△ABD=S△ABC,
又∵S△ABC=30,
∴S△ABD=×30=15,
又∵BE为△ABD的中线
∴S△BDE=S△ABD,
∴S△BDE=×15=,
∵EF⊥BC,且EF=5,
∴S△BDE= BD EF,
∴ BD×5=,
∴BD=3,
∴CD=BD=3.
【解析】【分析】(1)由∠ABE=∠ABC-∠EBD求出∠ABE的度数,由外角的性质可得∠BED=∠ABE+∠BAD,据此计算;
(2)根据等底同高三角形的面积相等得S△ABD=S△ABC=15,S△BDE=S△ABD=,根据三角形的面积公式可得BD,据此求解.
19.【答案】(1)解:若a>b,则a2>b2,是假命题,例如:0>﹣1,但02<(﹣1)2
(2)解:两个无理数的和仍是无理数,是假命题,例如:﹣ + =0,和是有理数
(3)解:若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形,是假命题,例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能够组成三角形。
【解析】【分析】(1)命题的真假,观察是否可以举出反例,使得题设推不出结论部分,当0>-1时,可证明命题为假。
(2)当两个无理数互为相反数时,两个无理数的和为0,可以证明命题为假命题。
(3)三角形的三边关系为,三角形任意两边之和大于第三边,任意两边之差小于第三边,所以命题可以被证明为假命题。
20.【答案】(1)
(2)1:2
(3)解:,,,
,
,
又,
,
即.
【解析】【解答】解:(1)如图1中,
,
,
;
故答案为:;
(2)如图2中,
,
,
;
故答案为:;
【分析】(1)根据即可求解;
(2)根据即可求解;
(3)由,即得,结合BP=AP,代入相应数据即可求解.
一、选择题
1.下列每组数分别表示三条线段长度,将它们首尾顺次相接能构成三角形的是( )
A.,, B.,, C.,, D.,,
2.如图,中AD为中线,,则与的周长之差为( )
A.1 B.2 C.3 D.4
3.三个内角的度数之比为3:4:5,那么是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
4.下列是命题的是( )
A.作两条相交直线 B.∠α和∠β相等吗?
C.全等三角形的对应边相等 D.若,求a的值
5.下列结论正确的是( )
A.有理数与数轴上的点一一对应 B.二次根式有意义条件是
C.立方根等于它本身是 D.如果,那么
6. 如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF,△BEF 的面积分别为 S△ABC,S△ADF,S△BEF,且 S△ABC=18,则 S△ADF﹣S△BEF( )
A.5 B.4 C.3 D.2
7.等腰三角形的一个角是,则它的底角是( )
A. B. C.或 D.或
8.如图,是的平分线,,,则( )
A. B. C. D.
9.下列命题的逆命题是真命题的是( )
A.两直线平行,内错角相等 B.如果,那么
C.钝角三角形中有两个锐角 D.对顶角相等
10.下列说法正确的个数是( )
①函数的图象不经过第三象限
②一组数据5,6,7,6,8,10的众数和中位数都是6
③将的图象沿y轴向下平移3个单位长度后,图象经过原点
④式子有意义的条件是且
A.1 B.2 C.3 D.4
二、填空题
11. 如图,是的一条中线,若,则 .
12.将命题“对顶角相等”用“如果…那么…”的形式可以改写为 .
13.如图,在中,点D、E、F分别是线段BC、AD、CE的中点,且,则 .
14.下列命题:①内错角相等;②平方根等于本身的数是0;③已知点A(2,3),B(2,﹣3),则直线AB∥y轴:④不等式组1<x<a的整数解只有1个,则a的取值范围为2<a≤3;其中是真命题的有: (填序号).
三、解答题
15. 如图,中,于点E,AF是的平分线,交BE于点F,,,求的度数.
16.如图,在中,,,是的角平分线,求的度数.
17.写出命题“等腰三角形两腰上的高线长相等”的逆命题,判断这个命题的真假,并说明理由.
四、综合题
18.如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABC=35°,∠EBD=18°,∠BAD=30°,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD的长度.
19.请判断下列命题的真假性,若是假命题,请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
20.等面积法是一种常用的、重要的数学解题方法.
(1)如图1,在中,,,,,,则的长为: .
(2)如图2,在中,,,则的高与的比是: .
(3)如图3,在中,,点D,P分别在边,上,且,,,垂足分别为点E,F.若,求的值.
答案解析部分
1.【答案】D
【解析】【解答】解:A:1+2<6,不能构成三角形,不符合题意;
B:2+2=4,不能构成三角形,不符合题意;
C:1+2=3,不能构成三角形,不符合题意;
D:2+3>4,能构成三角形,符合题意.
故答案为:D
【分析】根据三角形三边关系即可求出答案.
2.【答案】B
【解析】【解答】解:∵AD为△ABC的中线,
∴BD=DC,
∴=(AB+AD+BD)-(AC+AD+DC)=AB﹣AC=8﹣6=2,
故答案为:B.
【分析】根据三角形的中线的定义得到BD=DC,然后根据三角形的周长公式表示出两三角形的周长之差计算即可.
3.【答案】B
【解析】【解答】解:设这三个内角的度数分别为3x°,4x°,5x°.
则3x+4x+5x=180,
解得x=15,
∴5x°=75°,3x°=45°,4x°=60°,
所以这个三角形是锐角三角形,
故答案为:B.
【分析】已知三角形三个内角的度数之比,可以设这三个内角的度数分别为3x°,4x°,5x°,根据三角形的内角和等于180°列方程求解即可求出三个内角的度数,再从角的角度来判断三角形的形状.
4.【答案】C
【解析】【解答】解:A、“作两条相交直线”,它不是命题,所以A选项错误;
B、“∠α和∠β相等吗?”,它不是命题,所以A选项错误;
C、全等三角形对应边相等,它是命题,所以C选项正确;
D、“若a2=4,求a的值”,它不是命题,所以D选项错误.
故答案为:D.
【分析】根据命题的定义即:判断一件事情的语句叫做命题,逐个判断即可.
5.【答案】D
【解析】【解答】解:A.实数与数轴上的点一一对应,不符合题意;
B.二次根式有意义条件是全体实数,不符合题意;
C.立方根等于它本身是和0,不符合题意;
D.如果,那么,符合题意.
故答案为:D.
【分析】根据真命题的定义逐项判断即可。
6.【答案】C
7.【答案】D
【解析】【解答】解:当80°的角为顶角时,
底角=(180°-80°)=50°.
情况二:当80°的角为底角时,
80°2=160°,小于180°同样满足
它的底角是或
故答案为:D.
【分析】本题考察了等腰三角形的内角和,底角的知识点。
8.【答案】C
【解析】【解答】∵∠DAE=60°,
∴∠BAD=120°,
∵AD是∠CAE的平分线,
∴∠CAD=∠BAD=60°,
∴∠BAC=180°-∠CAE=180°-120°=60°,
∵∠B=35°,
∴∠D=180°-(∠BAC+∠CAD)-∠B=180°-120°-35°=25°,
∴∠ACB=∠CAD+∠D=60°+25°=85°,
故答案为:C.
【分析】先利用角平分线的定义求出∠CAD=∠BAD=60°,再利用角的运算求出∠D的度数,最后求出∠ACB的度数即可.
9.【答案】A
10.【答案】B
【解析】【解答】解:①∵,∴函数的图象经过一、二、四象限,不过第三象限,原说法符合题意;
②一组数据5,6,7,6,8,10重新排列后为5,6,6,7,8,10,众数是6,中位数是,原说法不符合题意;
③将的图象沿y轴向下平移3个单位长度后的解析式是:,图象不经过原点,原说法不符合题意;
④式子有意义的条件是且,原说法符合题意.
说法正确的有①④,共2个.
故答案为:B.
【分析】根据真命题的定义逐项判断即可。
11.【答案】10
【解析】【解答】解:∵是的一条中线,,
∴BC=2BD=10,
故答案为:10.
【分析】根据三角形的中线求出BC=2BD=10,即可作答。
12.【答案】如果两个角是对顶角,那么这两个角相等
【解析】【解答】解:命题“对顶角相等”用“如果…那么…”的形式可以改写为:如果两个角是对顶角,那么这两个角相等 ;
故答案为: 如果两个角是对顶角,那么这两个角相等 .
【分析】先找出命题的题设和结论,再写成“如果…那么…”的形式即可.
13.【答案】4
【解析】【解答】∵F为CE中点,
∴,
∵E为AD中点,
∴,
∴,
∵F为CE中点,
∴
故答案为:4.
【分析】由中点可以得到三角形的中线,可得到等底等高的三角形的面积相等,用△ABC的面积表示出△BDE和△CDE的面积,从而得到△BCE的面积,再由BF是△BEC的中线可得到△BEF的面积是△ABC的面积的一半,然后代入数据进行计算即可得解.
14.【答案】②③④
【解析】【解答】解:①两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
②平方根等于本身的数是0,正确,是真命题,符合题意;
③已知点A(2,3),B(2,﹣3),则直线AB∥y轴,正确,是真命题,符合题意;
④不等式组1<x<a的整数解只有1个,则a的取值范围为2<a≤3,正确,是真命题,符合题意.
故答案为:②③④.
【分析】根据平行线的性质“两直线平行,内错角相等”可判断①;根据平方根的性质“一个正数有两个平方根,这两个平方根互为相反数,负数没有平方根,0的平方根是0”可判断②;平行于y轴的直线上的点的横坐标相同,据此判断③;根据不等式组的整数解可得a的范围,据此判断④.
15.【答案】解:∵,,
∴.
∵AF是的平分线,
∴.
∵,
∴,
∴.
16.【答案】解:在中,
,,
,
是的角平分线,
,
【解析】【分析】从问题入手,要求的度数,根据三角形的外角和等于不相邻的两个内角和,就需要先求,由此要求,是三角形ABC的一个内角,其他2个内角已知,根据内角和是180°的性质可求,至此整理思路即可。
17.【答案】解:命题“等腰三角形两腰上的高线长相等”的逆命题是两边上的高相等的三角形为等腰三角形,此逆命题为真命题.
如图,在△ABC中,CD⊥AB,BE⊥AC,且CD=BE,
∵BC=BC,
∴△CBD≌△BCE(HL),
∴∠DBC=∠ECB,
∴△ABC为等腰三角形.
【解析】【分析】根据命题与逆命题的性质判断即可.
18.【答案】(1)解:∵∠ABC=35°,∠EBD=18°,
∴∠ABE=35°﹣18°=17°,
∴∠BED=∠ABE+∠BAD=17°+30°=47°
(2)解:∵AD是△ABC的中线,
∴S△ABD=S△ABC,
又∵S△ABC=30,
∴S△ABD=×30=15,
又∵BE为△ABD的中线
∴S△BDE=S△ABD,
∴S△BDE=×15=,
∵EF⊥BC,且EF=5,
∴S△BDE= BD EF,
∴ BD×5=,
∴BD=3,
∴CD=BD=3.
【解析】【分析】(1)由∠ABE=∠ABC-∠EBD求出∠ABE的度数,由外角的性质可得∠BED=∠ABE+∠BAD,据此计算;
(2)根据等底同高三角形的面积相等得S△ABD=S△ABC=15,S△BDE=S△ABD=,根据三角形的面积公式可得BD,据此求解.
19.【答案】(1)解:若a>b,则a2>b2,是假命题,例如:0>﹣1,但02<(﹣1)2
(2)解:两个无理数的和仍是无理数,是假命题,例如:﹣ + =0,和是有理数
(3)解:若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形,是假命题,例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能够组成三角形。
【解析】【分析】(1)命题的真假,观察是否可以举出反例,使得题设推不出结论部分,当0>-1时,可证明命题为假。
(2)当两个无理数互为相反数时,两个无理数的和为0,可以证明命题为假命题。
(3)三角形的三边关系为,三角形任意两边之和大于第三边,任意两边之差小于第三边,所以命题可以被证明为假命题。
20.【答案】(1)
(2)1:2
(3)解:,,,
,
,
又,
,
即.
【解析】【解答】解:(1)如图1中,
,
,
;
故答案为:;
(2)如图2中,
,
,
;
故答案为:;
【分析】(1)根据即可求解;
(2)根据即可求解;
(3)由,即得,结合BP=AP,代入相应数据即可求解.
