第3章 勾股定理 单元检测卷 (含答案) 2023—-2024学年苏科版数学八年级上册
文档属性
| 名称 | 第3章 勾股定理 单元检测卷 (含答案) 2023—-2024学年苏科版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 469.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 20:44:42 | ||
图片预览


文档简介
第3章《勾股定理》单元检测卷
2023-2024学年八年级上册数学苏科版
一、单选题(共10小题,满分40分)
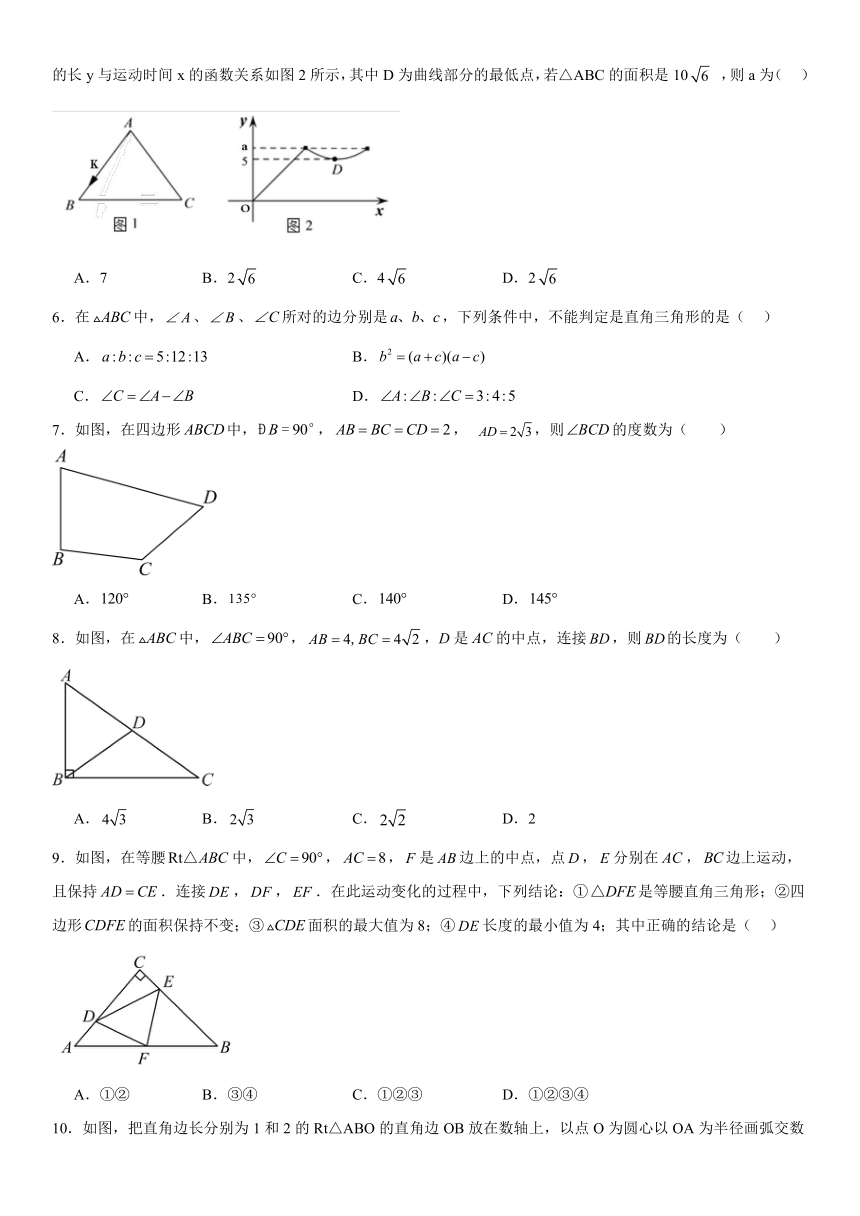
1.如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
A.2 B. C. D.3
2.如图,垂直地面的旗杆在离地3m处断裂,旗杆顶部落地点离旗杆底部4m,则旗杆折断前的高度为( )
A.6 B.7 C.8 D.9
3.图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7cm,则图中A、B两个正方形的面积之和为( )
A.28cm2 B.42cm2 C.49cm2 D.63cm2
4.如图,在由边长为1个单位长度的小正方形组成的网格中,线段的两个端点都在正方形网格的格点上,则的长度可能是( )
A. B. C. D.
5.如图1,动点K从△ABC的顶点A出发,沿AB→BC匀速运动到点C停止,在动点K运动过程中,线段AK的长y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,若△ABC的面积是10 ,则a为( )
A.7 B.2 C.4 D.2
6.在中,、、所对的边分别是,下列条件中,不能判定是直角三角形的是( )
A. B.
C. D.
7.如图,在四边形中,,, ,则的度数为( )
A. B. C. D.
8.如图,在中,,,D是的中点,连接,则的长度为( )
A. B. C. D.2
9.如图,在等腰中,,,是边上的中点,点,分别在,边上运动,且保持.连接,,.在此运动变化的过程中,下列结论:①是等腰直角三角形;②四边形的面积保持不变;③面积的最大值为8;④长度的最小值为4;其中正确的结论是( )
A.①② B.③④ C.①②③ D.①②③④
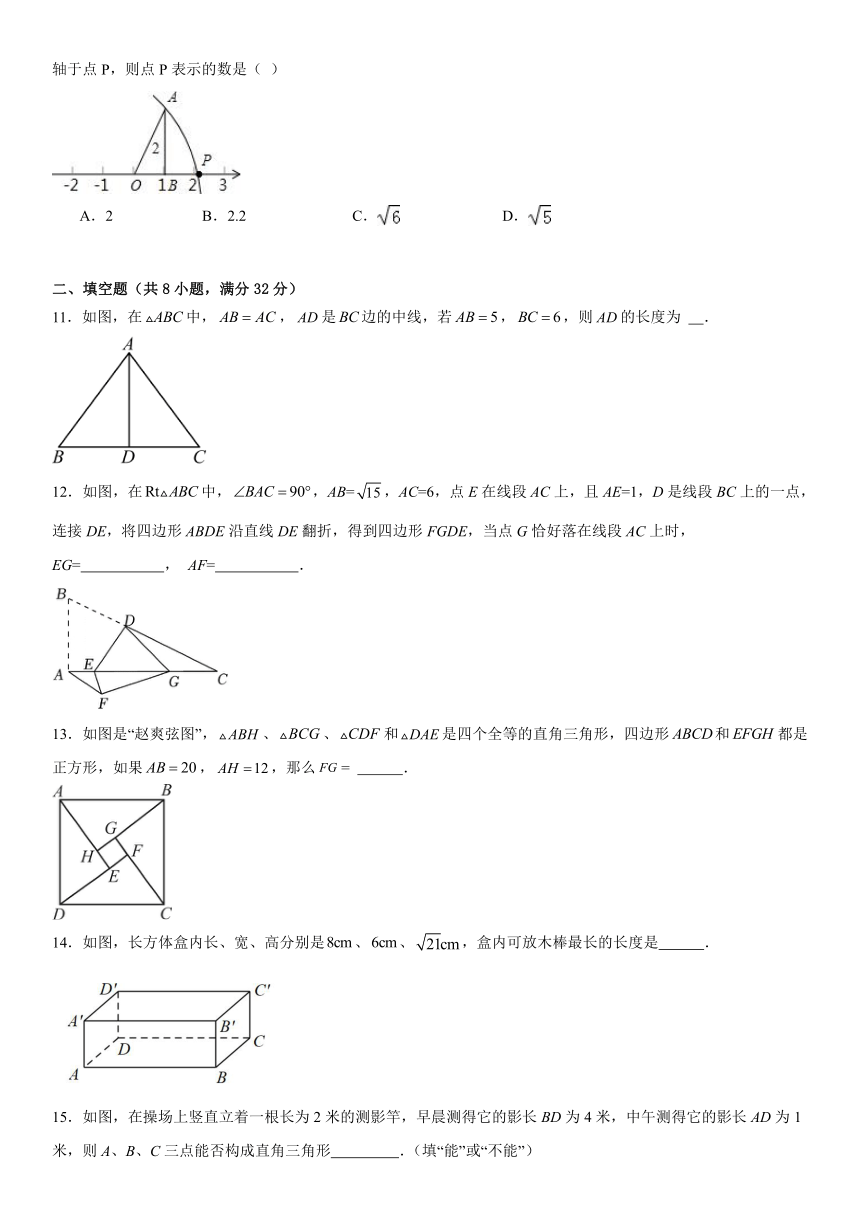
10.如图,把直角边长分别为1和2的Rt△ABO的直角边OB放在数轴上,以点O为圆心以OA为半径画弧交数轴于点P,则点P表示的数是( )
A.2 B.2.2 C. D.
二、填空题(共8小题,满分32分)
11.如图,在中,,是边的中线,若,,则的长度为 .
12.如图,在中,,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,EG= , AF= .
13.如图是“赵爽弦图”,、、和是四个全等的直角三角形,四边形和都是正方形,如果,,那么= .
14.如图,长方体盒内长、宽、高分别是、、,盒内可放木棒最长的长度是 .
15.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长BD为4米,中午测得它的影长AD为1米,则A、B、C三点能否构成直角三角形 .(填“能”或“不能”)
16.如图,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为 .
17.如图,四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”,如果大正方形面积为169,且直角三角形中较短的直角边的长为5,则中间小正方形面积(阴影部分)为 .
18.如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边作等边△DCE.B、E在C、D的同侧,若AB=,则BE= .
三、解答题(共6小题,每题8分,满分48分)
19.如图,某商场有一长为的货梯的倾斜角,为了改善货梯的安全性能,准备重新建造货梯,使其倾斜角.求调整后的货梯的长.
20.如图是一个的正方形网格,已知每个小正方形的边长均为1,每个小正方形的顶点称为格点,请按要求解答下列问题:
(1)如图,满足线段的格点共有______个;
(2)试在图中画出一个格点,使其为等腰三角形,,且的内部只包含4个格点(不包含在边上的格点).
21.如图,某港口位于东西方向的海岸线上.“综合执法1号”、“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻,“综合执法1号”每小时航行n mle,“综合执法2号”每小时航行n mle,它们离开港口一个半小时后分别位于点,处,且相距n mle.
(1)求,的长度;
(2)如果知道“综合执法1号”沿北偏东61°方向航行,能知道“综合执法2号”沿哪个方向航行吗?
22.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即ab×4+(b-a)2,从而得到等式c2=ab×4+(b-a)2,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题:
(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
23.已知中,,,.在射线上取一点,使得为等腰三角形,这样的三角形有几个?请你求的周长.
24.“最短路径问题”是数学中一类具有挑战性的问题.其实,数学史上也有不少相关的故事.如下即为其中较为经典的一则:古希腊有一位久负盛名的学者,名叫海伦.他精通数学,物理,聪慧过人.有一天,一位将军向他请教一个问题:如图①,将军从A地骑马出发,要到河边让马饮水,然后再回到B地的马棚,为使马走的路程最短,应该让马在什么地方饮水?
大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
如图②,作点B关于直线的对称点,连接与直线交于点P,连接,则的和最小.
请你在下列的阅读、理解、应用的过程中,完成解答.
理由:如图③,在直线上另取任一点,连接,,,
∵直线是点B,的对称轴,点P,在上,
∴______,______,(依据______)
∴______.
在中,∵,(依据______),
∴,即最小.
【归纳总结】
在解决上述问题的过程中,我们利用轴对称变换,把点A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点P为与的交点,即三点共线).
由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
【模型应用】
如图④,圆柱形玻璃杯,高为,底面周长为.在杯内离杯底的点C处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短路程为______.
参考答案:
1.C
2.C
3.C
4.B
5.A
6.D
7.B
8.B
9.C
10.D
11.4
12. 4
13.4
14./11厘米
15.能
16.4,6
17.49
18.1
19.
20.(1)3;(2)略.
21.(1)PQ为 24 n mile,PR为18 n mile;(2) “综合执法2号”沿北偏西29°航行.
22.(1)CD=
(2)
23.3个,32m或或
24.,,轴对称的性质,,三角形三边关系;【模型应用】17.
2023-2024学年八年级上册数学苏科版
一、单选题(共10小题,满分40分)
1.如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
A.2 B. C. D.3
2.如图,垂直地面的旗杆在离地3m处断裂,旗杆顶部落地点离旗杆底部4m,则旗杆折断前的高度为( )
A.6 B.7 C.8 D.9
3.图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7cm,则图中A、B两个正方形的面积之和为( )
A.28cm2 B.42cm2 C.49cm2 D.63cm2
4.如图,在由边长为1个单位长度的小正方形组成的网格中,线段的两个端点都在正方形网格的格点上,则的长度可能是( )
A. B. C. D.
5.如图1,动点K从△ABC的顶点A出发,沿AB→BC匀速运动到点C停止,在动点K运动过程中,线段AK的长y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,若△ABC的面积是10 ,则a为( )
A.7 B.2 C.4 D.2
6.在中,、、所对的边分别是,下列条件中,不能判定是直角三角形的是( )
A. B.
C. D.
7.如图,在四边形中,,, ,则的度数为( )
A. B. C. D.
8.如图,在中,,,D是的中点,连接,则的长度为( )
A. B. C. D.2
9.如图,在等腰中,,,是边上的中点,点,分别在,边上运动,且保持.连接,,.在此运动变化的过程中,下列结论:①是等腰直角三角形;②四边形的面积保持不变;③面积的最大值为8;④长度的最小值为4;其中正确的结论是( )
A.①② B.③④ C.①②③ D.①②③④
10.如图,把直角边长分别为1和2的Rt△ABO的直角边OB放在数轴上,以点O为圆心以OA为半径画弧交数轴于点P,则点P表示的数是( )
A.2 B.2.2 C. D.
二、填空题(共8小题,满分32分)
11.如图,在中,,是边的中线,若,,则的长度为 .
12.如图,在中,,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,EG= , AF= .
13.如图是“赵爽弦图”,、、和是四个全等的直角三角形,四边形和都是正方形,如果,,那么= .
14.如图,长方体盒内长、宽、高分别是、、,盒内可放木棒最长的长度是 .
15.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长BD为4米,中午测得它的影长AD为1米,则A、B、C三点能否构成直角三角形 .(填“能”或“不能”)
16.如图,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两条直角边的长分别为 .
17.如图,四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”,如果大正方形面积为169,且直角三角形中较短的直角边的长为5,则中间小正方形面积(阴影部分)为 .
18.如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边作等边△DCE.B、E在C、D的同侧,若AB=,则BE= .
三、解答题(共6小题,每题8分,满分48分)
19.如图,某商场有一长为的货梯的倾斜角,为了改善货梯的安全性能,准备重新建造货梯,使其倾斜角.求调整后的货梯的长.
20.如图是一个的正方形网格,已知每个小正方形的边长均为1,每个小正方形的顶点称为格点,请按要求解答下列问题:
(1)如图,满足线段的格点共有______个;
(2)试在图中画出一个格点,使其为等腰三角形,,且的内部只包含4个格点(不包含在边上的格点).
21.如图,某港口位于东西方向的海岸线上.“综合执法1号”、“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻,“综合执法1号”每小时航行n mle,“综合执法2号”每小时航行n mle,它们离开港口一个半小时后分别位于点,处,且相距n mle.
(1)求,的长度;
(2)如果知道“综合执法1号”沿北偏东61°方向航行,能知道“综合执法2号”沿哪个方向航行吗?
22.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即ab×4+(b-a)2,从而得到等式c2=ab×4+(b-a)2,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题:
(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
23.已知中,,,.在射线上取一点,使得为等腰三角形,这样的三角形有几个?请你求的周长.
24.“最短路径问题”是数学中一类具有挑战性的问题.其实,数学史上也有不少相关的故事.如下即为其中较为经典的一则:古希腊有一位久负盛名的学者,名叫海伦.他精通数学,物理,聪慧过人.有一天,一位将军向他请教一个问题:如图①,将军从A地骑马出发,要到河边让马饮水,然后再回到B地的马棚,为使马走的路程最短,应该让马在什么地方饮水?
大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
如图②,作点B关于直线的对称点,连接与直线交于点P,连接,则的和最小.
请你在下列的阅读、理解、应用的过程中,完成解答.
理由:如图③,在直线上另取任一点,连接,,,
∵直线是点B,的对称轴,点P,在上,
∴______,______,(依据______)
∴______.
在中,∵,(依据______),
∴,即最小.
【归纳总结】
在解决上述问题的过程中,我们利用轴对称变换,把点A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点P为与的交点,即三点共线).
由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
【模型应用】
如图④,圆柱形玻璃杯,高为,底面周长为.在杯内离杯底的点C处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短路程为______.
参考答案:
1.C
2.C
3.C
4.B
5.A
6.D
7.B
8.B
9.C
10.D
11.4
12. 4
13.4
14./11厘米
15.能
16.4,6
17.49
18.1
19.
20.(1)3;(2)略.
21.(1)PQ为 24 n mile,PR为18 n mile;(2) “综合执法2号”沿北偏西29°航行.
22.(1)CD=
(2)
23.3个,32m或或
24.,,轴对称的性质,,三角形三边关系;【模型应用】17.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
