济钢高中2015届高三第四次月考文科数学试题
文档属性
| 名称 | 济钢高中2015届高三第四次月考文科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 897.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-11 06:39:25 | ||
图片预览




文档简介
绝密★启用并使用完毕前
济钢高中2012级高三学年第四次月考
数学(文科)试题
说明:本试卷满分 150 分,考试时间: 120 分钟 2015/1
第I卷(选择题,共 50 分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量a=(1,m),b=(m,2),若ab,则实数m的值为
A. B. C. D.0
2.已知集合
(A) (B) (C) (D)(-1,1)
3.设命题p:函数y=sin2x
(A)P为真 (B) (C) (D)
4.已知P是圆上的动点,则P点到直线的距离为最小值为
(A)1 (B) (C)2 (D)
5.已知
(A)1 (B)2 (C)4 (D)8
6.某程序框图如图所示,该程序运行后,输出的值为31,
则a等于
(A)0 (B)1 (C)2 (D)3
7.已知的面积为2,在所在的平面内有两点P、Q,满足,则的面积为
(A) (B) (C)1 (D)2
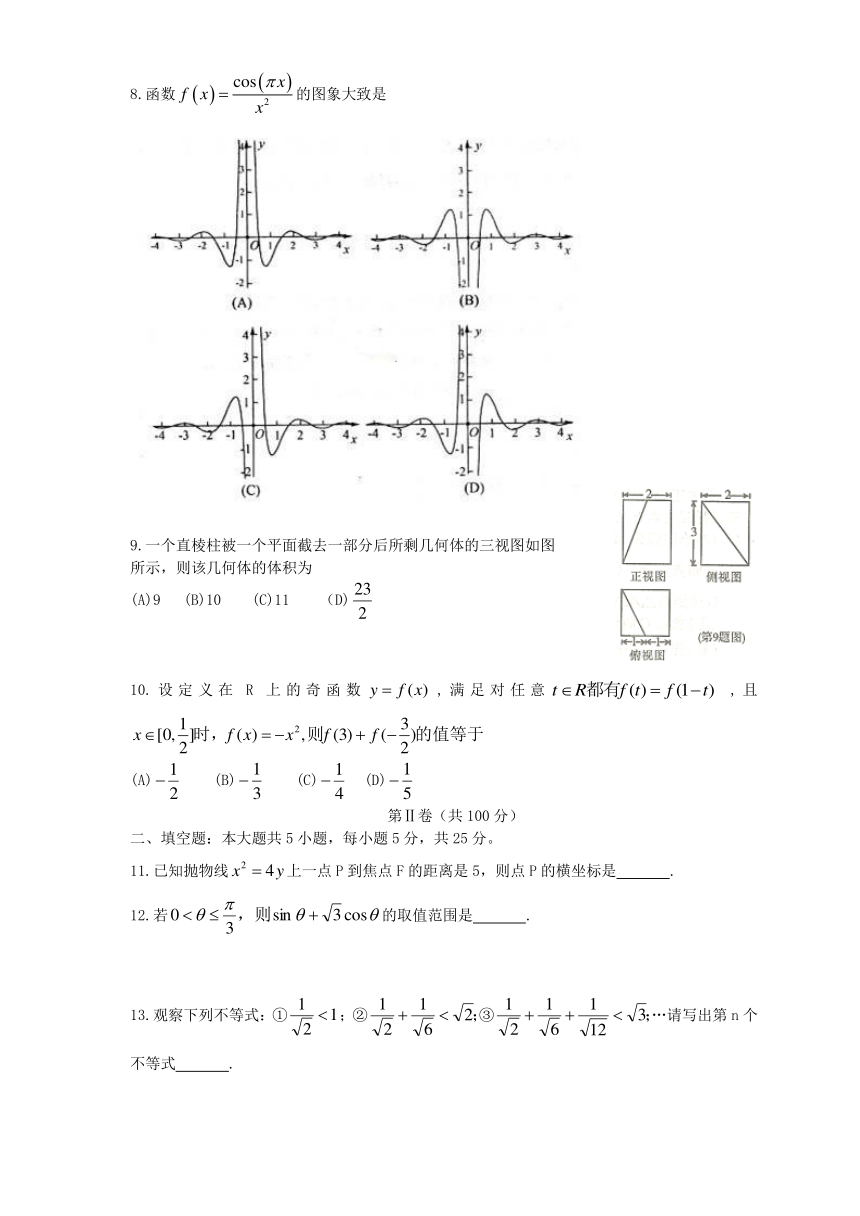
8.函数的图象大致是
9.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图
所示,则该几何体的体积为
(A)9 (B)10 (C)11 (D)
10.设定义在R上的奇函数,满足对任意 ,且
(A) (B) (C) (D)
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
11.已知抛物线上一点P到焦点F的距离是5,则点P的横坐标是 .
12.若的取值范围是 .
13.观察下列不等式:①;②③…请写出第n个不等式 .
14. 对任意实数a,b定义运算“”:设,若函数的图象与x轴恰有三个不同交点,则k的取值范围是 .
15.下列结论:
①直线a,b为异面直线的充要条件是直线a,b不相交;
②从总体中抽取的样本(),(),…,(),若,
则回归直线;
③函数;
④已知函数,则的图象关于直线x=2对称.
其中正确的结论是 .(注:把你认为正确结论的序号都填上)
三、解答题:本大题共6个小题,共75分。
16.(本小题满分12分)
已知向量,其中A,B,C分别为的三边a,b,c所对的角.
(I)求角C的大小;
(Ⅱ)若
17.(本小题满分12分)
某校举行环保知识竞赛,为了了解
本次竞赛成绩情况,从得分不低于
50分的试卷中随机抽取100名学生
的成绩(得分均为整数,满分100
分),进行统计,请根据频率分布表
中所提供的数据,解答下列问题:
(Ⅰ)求a、b的值;
(Ⅱ)若从成绩较好的第3、4、5组中,按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出 2人做负责人,求2人中至少有1人是第四组的概率。
18.(本小题满分12分)
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在的平面垂直,且DE//BC,
(I)证明:EO//平面ACD;
(II)证明:平面平面BCDE;
(III)求三棱锥E-ABD的体积.
19.(本小题满分12分)
设数列的前n项和为,点()在直线上.
(Ⅰ)求数列的通项公式;
(Ⅱ)在之间插入n个数,使这n+2个数公差为的等差数列,求数列的前n项和Tn.
20.(本小题满分13分)
设上的两点,已知向量,,若且椭圆的离心率短轴长为2,为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线过椭圆的焦点(0,c),(c为半焦距),求直线的斜率的值;
(Ⅲ)试问:的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
21.(本小题满分14分)
已知函数,令.
(Ⅰ)当a=0时,求的极值; (Ⅱ)若,讨论函数的单调性;
(Ⅲ)当-32012级高三第四次月考
数学(文科)试题答案
一.选择题BBCAD DBACC
17.
.
19.
20.(Ⅰ)
椭圆的方程为 ………………………………3分
(Ⅱ)由题意,设的方程为
由已知得:
……7分
(Ⅲ) (1)当直线AB斜率不存在时,即,由
………………………………8分
又 在椭圆上,所以
所以三角形的面积为定值. ……………………………………9分
(2)当直线AB斜率存在时:设AB的方程为y=kx+b
……………………………………10分
………………………………………12分
所以三角形的面积为定值. ………………………………………14分
DI
济钢高中2012级高三学年第四次月考
数学(文科)试题
说明:本试卷满分 150 分,考试时间: 120 分钟 2015/1
第I卷(选择题,共 50 分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量a=(1,m),b=(m,2),若ab,则实数m的值为
A. B. C. D.0
2.已知集合
(A) (B) (C) (D)(-1,1)
3.设命题p:函数y=sin2x
(A)P为真 (B) (C) (D)
4.已知P是圆上的动点,则P点到直线的距离为最小值为
(A)1 (B) (C)2 (D)
5.已知
(A)1 (B)2 (C)4 (D)8
6.某程序框图如图所示,该程序运行后,输出的值为31,
则a等于
(A)0 (B)1 (C)2 (D)3
7.已知的面积为2,在所在的平面内有两点P、Q,满足,则的面积为
(A) (B) (C)1 (D)2
8.函数的图象大致是
9.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图
所示,则该几何体的体积为
(A)9 (B)10 (C)11 (D)
10.设定义在R上的奇函数,满足对任意 ,且
(A) (B) (C) (D)
第Ⅱ卷(共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
11.已知抛物线上一点P到焦点F的距离是5,则点P的横坐标是 .
12.若的取值范围是 .
13.观察下列不等式:①;②③…请写出第n个不等式 .
14. 对任意实数a,b定义运算“”:设,若函数的图象与x轴恰有三个不同交点,则k的取值范围是 .
15.下列结论:
①直线a,b为异面直线的充要条件是直线a,b不相交;
②从总体中抽取的样本(),(),…,(),若,
则回归直线;
③函数;
④已知函数,则的图象关于直线x=2对称.
其中正确的结论是 .(注:把你认为正确结论的序号都填上)
三、解答题:本大题共6个小题,共75分。
16.(本小题满分12分)
已知向量,其中A,B,C分别为的三边a,b,c所对的角.
(I)求角C的大小;
(Ⅱ)若
17.(本小题满分12分)
某校举行环保知识竞赛,为了了解
本次竞赛成绩情况,从得分不低于
50分的试卷中随机抽取100名学生
的成绩(得分均为整数,满分100
分),进行统计,请根据频率分布表
中所提供的数据,解答下列问题:
(Ⅰ)求a、b的值;
(Ⅱ)若从成绩较好的第3、4、5组中,按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出 2人做负责人,求2人中至少有1人是第四组的概率。
18.(本小题满分12分)
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在的平面垂直,且DE//BC,
(I)证明:EO//平面ACD;
(II)证明:平面平面BCDE;
(III)求三棱锥E-ABD的体积.
19.(本小题满分12分)
设数列的前n项和为,点()在直线上.
(Ⅰ)求数列的通项公式;
(Ⅱ)在之间插入n个数,使这n+2个数公差为的等差数列,求数列的前n项和Tn.
20.(本小题满分13分)
设上的两点,已知向量,,若且椭圆的离心率短轴长为2,为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线过椭圆的焦点(0,c),(c为半焦距),求直线的斜率的值;
(Ⅲ)试问:的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
21.(本小题满分14分)
已知函数,令.
(Ⅰ)当a=0时,求的极值; (Ⅱ)若,讨论函数的单调性;
(Ⅲ)当-3
数学(文科)试题答案
一.选择题BBCAD DBACC
17.
.
19.
20.(Ⅰ)
椭圆的方程为 ………………………………3分
(Ⅱ)由题意,设的方程为
由已知得:
……7分
(Ⅲ) (1)当直线AB斜率不存在时,即,由
………………………………8分
又 在椭圆上,所以
所以三角形的面积为定值. ……………………………………9分
(2)当直线AB斜率存在时:设AB的方程为y=kx+b
……………………………………10分
………………………………………12分
所以三角形的面积为定值. ………………………………………14分
DI
同课章节目录
