4.2立方根 课件(共28张PPT)八年级数学上册苏科版
文档属性
| 名称 | 4.2立方根 课件(共28张PPT)八年级数学上册苏科版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 22:45:07 | ||
图片预览







文档简介
(共28张PPT)
第4章 · 平方根
4.2 立方根
学习目标
1. 了解立方根的概念,会用根号表示数的立方根;
2. 了解开立方与立方是互逆的运算,会用立方运算求一些数的立方根;
3. 能运用立方根解决一些简单的实际问题.
传说中,公元前429年,一场瘟疫袭击了希腊第罗斯岛(Delos),造成四分之一的人口死亡.岛民们推派一些代表去神庙请示阿波罗的旨意,神指示说:要想遏止瘟疫,得将阿波罗神殿中那正立方的祭坛加大一倍.人们便把每边增长一倍送到神那儿,于是神更加发火,他说,你们竟敢愚弄我!我要加倍惩罚你们!第罗斯岛人只好去求救于当时著名的学者柏拉图.
数学小故事
倍立方问题
开始,柏拉图和他的学生认为这个问题很容易,试图用尺规作图作出它,均告失败,最后才发现这是一个尺规作图不能成功的问题.
探索与交流
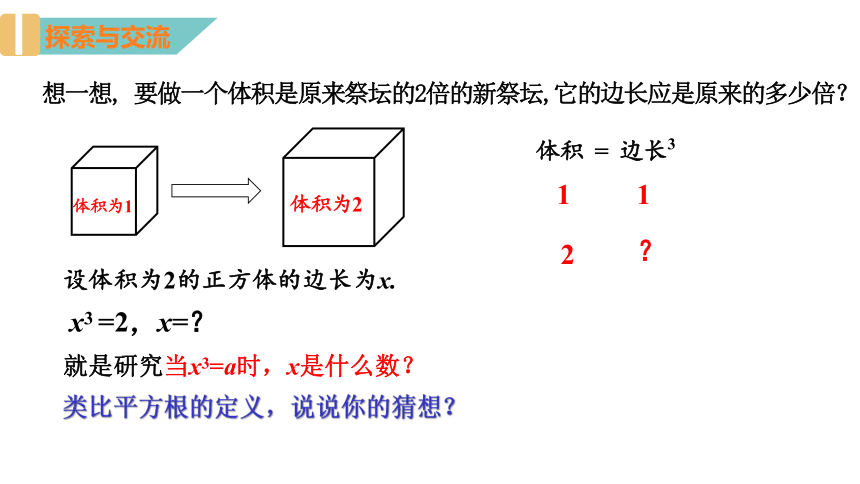
想一想, 要做一个体积是原来祭坛的2倍的新祭坛,它的边长应是原来的多少倍?
体积为1
体积为2
体积 = 边长3
1
1
2
?
设体积为2的正方体的边长为x.
x3 =2,x=?
类比平方根的定义,说说你的猜想?
就是研究当x3=a时,x是什么数?
一般地,如果 x3=a ,那么x叫做a的立方根,也称为三次方根.
立方根的定义:
概念学习
23=8
____是8的立方根
2
33=27
____是27的立方根
3
立方根用什么符号表示呢?
8的立方根是2
27的立方根是3
3
读作:
三次根号
记作:
记作:
x3 =2,x=
定义:求一个数的立方根的运算叫做开立方.
概念学习
开立方与立方互为逆运算,所以可以通过立方运算来求一个数的立方根.
x3 = a
x
立方
a
开立方
立方根
幂
a
x
检验x是不是a的立方根,只要看x3是不是等于a即可.
(1) ∵ 43=64, ∴ 64的立方根是4,即=4.
(2)∵(-)3 = -,∴-的立方根是-,即 = -.
(3) 9的立方根是.
(4) ∵ 0.63=0.216, ∴ 0.216的立方根是0.6,即=0.6.
(5) ∵(-3)3=-27,所以-27的立方根是-3,即= -3.
例题讲解
例1 求下列各数的立方根:
(1)64; (2)- ; (3)9 (4)0.216 (5)(-3)3
解:
新知巩固
-27,0.008,,-1,0.064,4.
1.写出下列各数的立方根:
= -3,
= 0.2,
= ,
=-1,
= 0.4,
.
解:
(1); (2)±; (3); (4).
2.求下列各式的值.
新知巩固
= ,
(2)± =± 0.6,
(3)= 10,
==.
解:
新知巩固
(3)(x-1)3=125.
3.求下列各式中的x:
(1)8x3=27;
(2)-27x3=64;
(3) ∵ 53=125,
∴ x-1=5,
∴ x=6.
解:
(1)两边同时除以8,得
x3= .
∵()3= ,
∴x= .
(2)两边同时除以-27,得
x3=-.
∵ = -,
∴ x= -.
立方根与平方根的区别与联系:
平方根 立方根
区 别
联系 关 系
名 称
概念不同
如果x2=a (a≥0),那么x叫做a的平方根,也称为二次方根.
如果 x3=a ,那么x叫做a的立方根,也称为三次方根.
个数不同
一个正数有两个平方根,它们互为相反数.
一个正数有一个正的立方根;
一个负数有一个负的立方根
表示方法不同
±
被开方数的取值范围不同
被开方数是非负数,即 a≥0
被开方数是任意数
运算关系
开方运算与相应的乘方运算互为逆运算
转化条件
都可以转化为非负数的非负方根来研究
类比归纳
0
0的平方根和立方根都是0
例2 把一个长12 cm,宽9 cm,高2 cm的长方体铁坯加工成一个正方体铁锭后,表面积有什么变化?(加工过程中无损失)
解:长方体的表面积为(12×9+9×2+12×2)×2=300(cm2).
设正方体的棱长为x cm,则
x3=12×9×2,解得x=6 .
∴正方体的表面积为6×62=216(cm2) .
300-216=84(cm2),
∴表面积减少了84 cm2.
例题讲解
新知巩固
1.两个球形探空气球的体积分别约为5 120 m3和80 m3,试计算它们的半径比(球的体积公式:V球=R3,R为球的半径).
解:由球的体积公式可知:
2. 已知a+1的算术平方根是3,﹣27的立方根是b-12,c-3的平方根是±2.
求:(1)a,b,c的值;(2)a+4b﹣4c的立方根.
解:(1)∵a+1的算术平方根是3,
∴a+1=9,a=8;
∵-27的立方根是b-12,
∴b-12=-3,b=9;
∵c-3的平方根是±2,
∴c-3=4,c=7;
即a,b,c的值分别为8,9,7;
新知巩固
(2)由(1)知,a+4b-4c=8+4×9-4×7=16,
∴a+4b-4c的立方根是.
=
探索与交流
下列各数有立方根吗?如果有,请写出来;如果没有,请说明理由.
, 0.001, 9,-3,-64,- , 0.
= 0. 1
=-4
=
= 0
=
=
=
=
这几个式子有什么共同特征?
新知归纳
正数的立方根是正数;
0的立方根是0.
负数的立方根是负数;
立方根的性质:
= a
a的取值范围是什么?
①,-; ②,-; ③,-.
拓展延伸
1. 求下列各式的值:
通过上述计算,你能发现什么规律?
①= -,-= -;
②= -4,-= -4;
③=-,-=-.
解:
=-
拓展延伸
2. 填空:
①=__________; ② =__________;
③ =___________; ④ =__________.
27
-8
∵x3=a ,x=
∴()3=a
2
-3
通过以上计算,你发现了什么规律?
()3=a
新知归纳
立方根的三个性质:
= a
()3=a
=-
课堂小结
立方根
概念与表示方法
性质
运算
正数的立方根是正数
负数的立方根是负数
0的立方根是0
开立方
1.-27的立方根为( )
A.±3 B.±9 C.-3 D.-9
当堂检测
C
2.下列语句中,正确的是( )
A.的立方根是±2 B.±是1的立方根
C.-3是27的负立方根 D.(-2)3的立方根是-2
D
当堂检测
3.下列说法正确的是 ( )
A.如果一个数的立方根是这个数本身,那么这个数一定是0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个数的立方根与这个数同号,0的立方根是0
D
4.下列各式错误的是( )
A. =0.2 B. =- C. =± D. =-102
C
当堂检测
5. 平方根等于它本身的数有_____,立方根等于它本身的数有________;
0
6. 体积是125 dm3的正方体的棱长是________dm.
5.5
7.如果的平方根是±3,则=_______.
解:∵的平方根是,
∴,
∴,
∴.
4
-1、0、1
当堂检测
a 0.000001 0.001 1 1000 1000000
(2)根据你发现的规律填空:
已知≈1.442,则≈________, ≈__________.
8. (1)填表:
0.01
0.1
1
10
100
14.42
-0.1442
=-144.2,则x= ___________.
-3 000 000
当堂检测
9.求下列各式中的x:
解:x3-64=0,
移项,得x3=64,
解得x=4.
(2)(x+1)3=-8.
(1) x3-64=0;
(x+1)3=-8,
可得x+1=-2,
解得x=-3.
10. 某校在开展劳动教育剪纸课的时候,问同学们,你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼起来作为纸盒的盖.如果我们希望做成的长方体的体积为32cm2,那么整张大正方形纸片的边长应是多少?
解:设小正方形的边长为x,
则由小正方形拼接成的大正方形边长为 ,
作原料的大正方形的边长为,
根据题意可得:,
解得:,
∴,
答:作原料的大正方形的边长为.
当堂检测
当堂检测
11. 已知与的值互为相反数,求代数式的值.
解:由题意,得(1-2x)+(3y-2)=0,
整理,得2x+1=3y,
所以==1.
当堂检测
12. 已知2a-1的平方根是±3,3a+b+1的立方根是3.
(1)求a,b的值;
(2)求a+b的算术平方根.
(2)由(1)可得a+b=16,
∴a+b的算术平方根为4.
解:
(1)由题意得:
第4章 · 平方根
4.2 立方根
学习目标
1. 了解立方根的概念,会用根号表示数的立方根;
2. 了解开立方与立方是互逆的运算,会用立方运算求一些数的立方根;
3. 能运用立方根解决一些简单的实际问题.
传说中,公元前429年,一场瘟疫袭击了希腊第罗斯岛(Delos),造成四分之一的人口死亡.岛民们推派一些代表去神庙请示阿波罗的旨意,神指示说:要想遏止瘟疫,得将阿波罗神殿中那正立方的祭坛加大一倍.人们便把每边增长一倍送到神那儿,于是神更加发火,他说,你们竟敢愚弄我!我要加倍惩罚你们!第罗斯岛人只好去求救于当时著名的学者柏拉图.
数学小故事
倍立方问题
开始,柏拉图和他的学生认为这个问题很容易,试图用尺规作图作出它,均告失败,最后才发现这是一个尺规作图不能成功的问题.
探索与交流
想一想, 要做一个体积是原来祭坛的2倍的新祭坛,它的边长应是原来的多少倍?
体积为1
体积为2
体积 = 边长3
1
1
2
?
设体积为2的正方体的边长为x.
x3 =2,x=?
类比平方根的定义,说说你的猜想?
就是研究当x3=a时,x是什么数?
一般地,如果 x3=a ,那么x叫做a的立方根,也称为三次方根.
立方根的定义:
概念学习
23=8
____是8的立方根
2
33=27
____是27的立方根
3
立方根用什么符号表示呢?
8的立方根是2
27的立方根是3
3
读作:
三次根号
记作:
记作:
x3 =2,x=
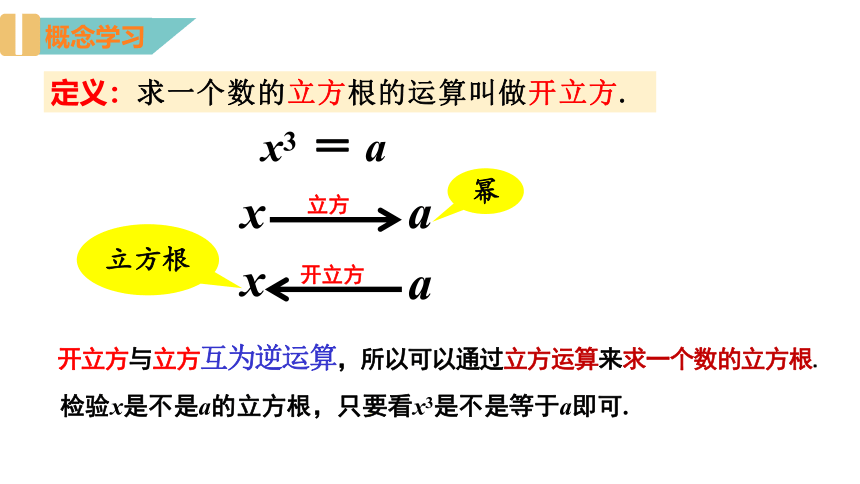
定义:求一个数的立方根的运算叫做开立方.
概念学习
开立方与立方互为逆运算,所以可以通过立方运算来求一个数的立方根.
x3 = a
x
立方
a
开立方
立方根
幂
a
x
检验x是不是a的立方根,只要看x3是不是等于a即可.
(1) ∵ 43=64, ∴ 64的立方根是4,即=4.
(2)∵(-)3 = -,∴-的立方根是-,即 = -.
(3) 9的立方根是.
(4) ∵ 0.63=0.216, ∴ 0.216的立方根是0.6,即=0.6.
(5) ∵(-3)3=-27,所以-27的立方根是-3,即= -3.
例题讲解
例1 求下列各数的立方根:
(1)64; (2)- ; (3)9 (4)0.216 (5)(-3)3
解:
新知巩固
-27,0.008,,-1,0.064,4.
1.写出下列各数的立方根:
= -3,
= 0.2,
= ,
=-1,
= 0.4,
.
解:
(1); (2)±; (3); (4).
2.求下列各式的值.
新知巩固
= ,
(2)± =± 0.6,
(3)= 10,
==.
解:
新知巩固
(3)(x-1)3=125.
3.求下列各式中的x:
(1)8x3=27;
(2)-27x3=64;
(3) ∵ 53=125,
∴ x-1=5,
∴ x=6.
解:
(1)两边同时除以8,得
x3= .
∵()3= ,
∴x= .
(2)两边同时除以-27,得
x3=-.
∵ = -,
∴ x= -.
立方根与平方根的区别与联系:
平方根 立方根
区 别
联系 关 系
名 称
概念不同
如果x2=a (a≥0),那么x叫做a的平方根,也称为二次方根.
如果 x3=a ,那么x叫做a的立方根,也称为三次方根.
个数不同
一个正数有两个平方根,它们互为相反数.
一个正数有一个正的立方根;
一个负数有一个负的立方根
表示方法不同
±
被开方数的取值范围不同
被开方数是非负数,即 a≥0
被开方数是任意数
运算关系
开方运算与相应的乘方运算互为逆运算
转化条件
都可以转化为非负数的非负方根来研究
类比归纳
0
0的平方根和立方根都是0
例2 把一个长12 cm,宽9 cm,高2 cm的长方体铁坯加工成一个正方体铁锭后,表面积有什么变化?(加工过程中无损失)
解:长方体的表面积为(12×9+9×2+12×2)×2=300(cm2).
设正方体的棱长为x cm,则
x3=12×9×2,解得x=6 .
∴正方体的表面积为6×62=216(cm2) .
300-216=84(cm2),
∴表面积减少了84 cm2.
例题讲解
新知巩固
1.两个球形探空气球的体积分别约为5 120 m3和80 m3,试计算它们的半径比(球的体积公式:V球=R3,R为球的半径).
解:由球的体积公式可知:
2. 已知a+1的算术平方根是3,﹣27的立方根是b-12,c-3的平方根是±2.
求:(1)a,b,c的值;(2)a+4b﹣4c的立方根.
解:(1)∵a+1的算术平方根是3,
∴a+1=9,a=8;
∵-27的立方根是b-12,
∴b-12=-3,b=9;
∵c-3的平方根是±2,
∴c-3=4,c=7;
即a,b,c的值分别为8,9,7;
新知巩固
(2)由(1)知,a+4b-4c=8+4×9-4×7=16,
∴a+4b-4c的立方根是.
=
探索与交流
下列各数有立方根吗?如果有,请写出来;如果没有,请说明理由.
, 0.001, 9,-3,-64,- , 0.
= 0. 1
=-4
=
= 0
=
=
=
=
这几个式子有什么共同特征?
新知归纳
正数的立方根是正数;
0的立方根是0.
负数的立方根是负数;
立方根的性质:
= a
a的取值范围是什么?
①,-; ②,-; ③,-.
拓展延伸
1. 求下列各式的值:
通过上述计算,你能发现什么规律?
①= -,-= -;
②= -4,-= -4;
③=-,-=-.
解:
=-
拓展延伸
2. 填空:
①=__________; ② =__________;
③ =___________; ④ =__________.
27
-8
∵x3=a ,x=
∴()3=a
2
-3
通过以上计算,你发现了什么规律?
()3=a
新知归纳
立方根的三个性质:
= a
()3=a
=-
课堂小结
立方根
概念与表示方法
性质
运算
正数的立方根是正数
负数的立方根是负数
0的立方根是0
开立方
1.-27的立方根为( )
A.±3 B.±9 C.-3 D.-9
当堂检测
C
2.下列语句中,正确的是( )
A.的立方根是±2 B.±是1的立方根
C.-3是27的负立方根 D.(-2)3的立方根是-2
D
当堂检测
3.下列说法正确的是 ( )
A.如果一个数的立方根是这个数本身,那么这个数一定是0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个数的立方根与这个数同号,0的立方根是0
D
4.下列各式错误的是( )
A. =0.2 B. =- C. =± D. =-102
C
当堂检测
5. 平方根等于它本身的数有_____,立方根等于它本身的数有________;
0
6. 体积是125 dm3的正方体的棱长是________dm.
5.5
7.如果的平方根是±3,则=_______.
解:∵的平方根是,
∴,
∴,
∴.
4
-1、0、1
当堂检测
a 0.000001 0.001 1 1000 1000000
(2)根据你发现的规律填空:
已知≈1.442,则≈________, ≈__________.
8. (1)填表:
0.01
0.1
1
10
100
14.42
-0.1442
=-144.2,则x= ___________.
-3 000 000
当堂检测
9.求下列各式中的x:
解:x3-64=0,
移项,得x3=64,
解得x=4.
(2)(x+1)3=-8.
(1) x3-64=0;
(x+1)3=-8,
可得x+1=-2,
解得x=-3.
10. 某校在开展劳动教育剪纸课的时候,问同学们,你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼起来作为纸盒的盖.如果我们希望做成的长方体的体积为32cm2,那么整张大正方形纸片的边长应是多少?
解:设小正方形的边长为x,
则由小正方形拼接成的大正方形边长为 ,
作原料的大正方形的边长为,
根据题意可得:,
解得:,
∴,
答:作原料的大正方形的边长为.
当堂检测
当堂检测
11. 已知与的值互为相反数,求代数式的值.
解:由题意,得(1-2x)+(3y-2)=0,
整理,得2x+1=3y,
所以==1.
当堂检测
12. 已知2a-1的平方根是±3,3a+b+1的立方根是3.
(1)求a,b的值;
(2)求a+b的算术平方根.
(2)由(1)可得a+b=16,
∴a+b的算术平方根为4.
解:
(1)由题意得:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
