25.2.2 频率与概率 课件(共20张PPT) 九年级数学上册 (华东师大版)
文档属性
| 名称 | 25.2.2 频率与概率 课件(共20张PPT) 九年级数学上册 (华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 23:37:14 | ||
图片预览







文档简介
(共20张PPT)
第25章 随机事件的概率
华师版(2012)九年级上册数学
频率与概率
|25.2 随机事件的概率 第2课时 |
知识回顾
2.必然事件 A,则 P(A)=1;
不可能事件 B,则 P(B)=0;
随机事件 C,则 0<P(C)<1.
1.概率的定义及基本性质
如果在一次实验中,有 n 种可能的结果,并且他们发生的可能性都相等事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0≤m≤n,有0≤ ≤1
新知探究
活动一 小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得 1 分,为偶数我得 1 分,先得到 10 分的获胜”.如果你是小亮,你愿意接受这个游戏的规则吗
1 2 3 4 5 6
1
2
3
4
5
6
红桃
黑桃
用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
解:它可能出现的结果有 36 个,
满足两张牌的数字之积为奇数(记为事件 A)的有
9 种情况,
所以 P(A) = .
知识要点1
列表法
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
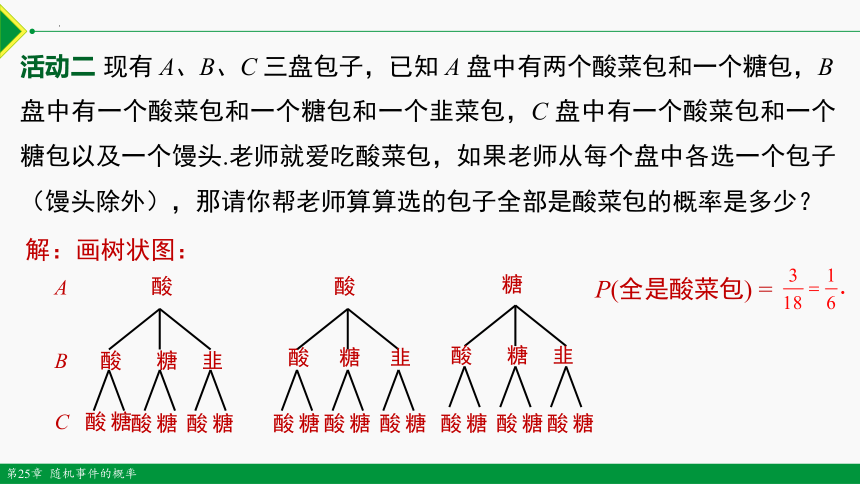
活动二 现有 A、B、C 三盘包子,已知 A 盘中有两个酸菜包和一个糖包,B 盘中有一个酸菜包和一个糖包和一个韭菜包,C 盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
韭
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
解:画树状图:
P(全是酸菜包) =
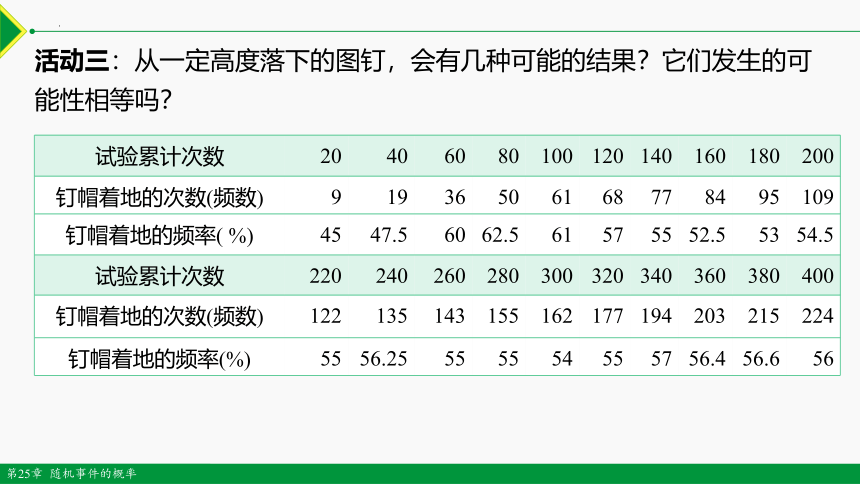
活动三:从一定高度落下的图钉,会有几种可能的结果?它们发生的可能性相等吗?
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
知识要点2
等可能事件概率的求法
1.(1)试验法的前提:结果不是有限个或可能性不相等
(2)试验法的条件:相同条件下进行,次数足够多;
(3)试验法的特征:频率和概率在试验中可以非常接近,但不一定相等,每次试验的结果可能不一样.
2.(1)理论分析法的前提:结果数有限且可能性相等;
(2)理论分析法的条件:确定需要的事件包含的结果数m和总的结果数n;
(3)理论分析法的结果:用P(A)= 计算出唯一确定结果
典例讲解
例1 班级里有20位女同学和22位男同学,班上每位同学的名字都被分别写在一张小纸条上,放入一个盒中搅匀.如果老师随机地从盒中取出1张纸条, 那么抽到男同学名字的概率大还是抽到女同学名字的概率大?
解:P(抽到男同学名字)
P(抽到女同学的名字)
因为
所以抽到男同学名字的概率大.
例2 某水果公司以2元/千克的成本新进了10 000千克柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,约定价为每千克大多少元比较合适
柑橘总质量(n)/千克 损坏柑橘质量(m)/千克 柑橘损坏的频率
50 5.50 0.110
100 10.5 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
从上表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为______.
0.1
稳定
0.9
解:根据估计的概率可以知道,在 10 000 kg 柑橘中完好柑橘的质量为
10 000×0.9=9 000(kg).
设每千克柑橘售价为 x 元,则
9 000x -2×10 000=5 000.
解得
x ≈ 2.8(元).
答:出售柑橘时,每千克大约定价 2.8 元可获利润 5 000元.
课堂小结
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
当一次试验要涉及两个以上因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用画树状图的办法.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.
课堂练习
1.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
2.如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.下面有三个推断,其中合理的是( )
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620
A.① B.② C.①② D.①③
B
3.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转,如果这三种可能性的大小相同.三辆汽车经过这个十字路口,(画树状图)求下列事件的概率:
(1)三辆汽车继续直行的概率;
(2)两辆车向右转,一辆车向左转的概率;
(3)至少有两辆车向左转的概率.
解:画树状图得:
.
(1)∴三辆汽车继续直行的概率为: ;
(2)两辆车向右转,一辆车向左转的概率为 ;
(3)至少有两辆车向左转的概率为: .
4.如图,甲、乙用 4 张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.
解:画树状图得:
∵共有 12 种等可能的结果,甲抽到的牌面数字比乙大的有 5 种情况,小于等于乙的有 7 种情况,
∴P(甲胜) = ,P(乙胜) = .
∴甲、乙获胜的机会不相同.
第25章 随机事件的概率
华师版(2012)九年级上册数学
频率与概率
|25.2 随机事件的概率 第2课时 |
知识回顾
2.必然事件 A,则 P(A)=1;
不可能事件 B,则 P(B)=0;
随机事件 C,则 0<P(C)<1.
1.概率的定义及基本性质
如果在一次实验中,有 n 种可能的结果,并且他们发生的可能性都相等事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0≤m≤n,有0≤ ≤1
新知探究
活动一 小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得 1 分,为偶数我得 1 分,先得到 10 分的获胜”.如果你是小亮,你愿意接受这个游戏的规则吗
1 2 3 4 5 6
1
2
3
4
5
6
红桃
黑桃
用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
解:它可能出现的结果有 36 个,
满足两张牌的数字之积为奇数(记为事件 A)的有
9 种情况,
所以 P(A) = .
知识要点1
列表法
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
活动二 现有 A、B、C 三盘包子,已知 A 盘中有两个酸菜包和一个糖包,B 盘中有一个酸菜包和一个糖包和一个韭菜包,C 盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
韭
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
解:画树状图:
P(全是酸菜包) =
活动三:从一定高度落下的图钉,会有几种可能的结果?它们发生的可能性相等吗?
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
知识要点2
等可能事件概率的求法
1.(1)试验法的前提:结果不是有限个或可能性不相等
(2)试验法的条件:相同条件下进行,次数足够多;
(3)试验法的特征:频率和概率在试验中可以非常接近,但不一定相等,每次试验的结果可能不一样.
2.(1)理论分析法的前提:结果数有限且可能性相等;
(2)理论分析法的条件:确定需要的事件包含的结果数m和总的结果数n;
(3)理论分析法的结果:用P(A)= 计算出唯一确定结果
典例讲解
例1 班级里有20位女同学和22位男同学,班上每位同学的名字都被分别写在一张小纸条上,放入一个盒中搅匀.如果老师随机地从盒中取出1张纸条, 那么抽到男同学名字的概率大还是抽到女同学名字的概率大?
解:P(抽到男同学名字)
P(抽到女同学的名字)
因为
所以抽到男同学名字的概率大.
例2 某水果公司以2元/千克的成本新进了10 000千克柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,约定价为每千克大多少元比较合适
柑橘总质量(n)/千克 损坏柑橘质量(m)/千克 柑橘损坏的频率
50 5.50 0.110
100 10.5 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
从上表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为______.
0.1
稳定
0.9
解:根据估计的概率可以知道,在 10 000 kg 柑橘中完好柑橘的质量为
10 000×0.9=9 000(kg).
设每千克柑橘售价为 x 元,则
9 000x -2×10 000=5 000.
解得
x ≈ 2.8(元).
答:出售柑橘时,每千克大约定价 2.8 元可获利润 5 000元.
课堂小结
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表的办法.
当一次试验要涉及两个以上因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用画树状图的办法.
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.
课堂练习
1.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
2.如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.下面有三个推断,其中合理的是( )
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620
A.① B.② C.①② D.①③
B
3.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转,如果这三种可能性的大小相同.三辆汽车经过这个十字路口,(画树状图)求下列事件的概率:
(1)三辆汽车继续直行的概率;
(2)两辆车向右转,一辆车向左转的概率;
(3)至少有两辆车向左转的概率.
解:画树状图得:
.
(1)∴三辆汽车继续直行的概率为: ;
(2)两辆车向右转,一辆车向左转的概率为 ;
(3)至少有两辆车向左转的概率为: .
4.如图,甲、乙用 4 张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.
解:画树状图得:
∵共有 12 种等可能的结果,甲抽到的牌面数字比乙大的有 5 种情况,小于等于乙的有 7 种情况,
∴P(甲胜) = ,P(乙胜) = .
∴甲、乙获胜的机会不相同.
