【高考调研】2015高中数学(人教A版)选修2-2:第二章 推理与证明 单元测试题
文档属性
| 名称 | 【高考调研】2015高中数学(人教A版)选修2-2:第二章 推理与证明 单元测试题 |  | |
| 格式 | zip | ||
| 文件大小 | 41.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-11 07:13:28 | ||
图片预览



文档简介
第二章 单元测试题
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知扇形的孤长为l,半径为r,类比三角形的面积公式S=,可知扇形面积公式( )
A. B.
C. D.不可类比
答案 C
解析 可以将扇形看作曲边三角形,所以选C.
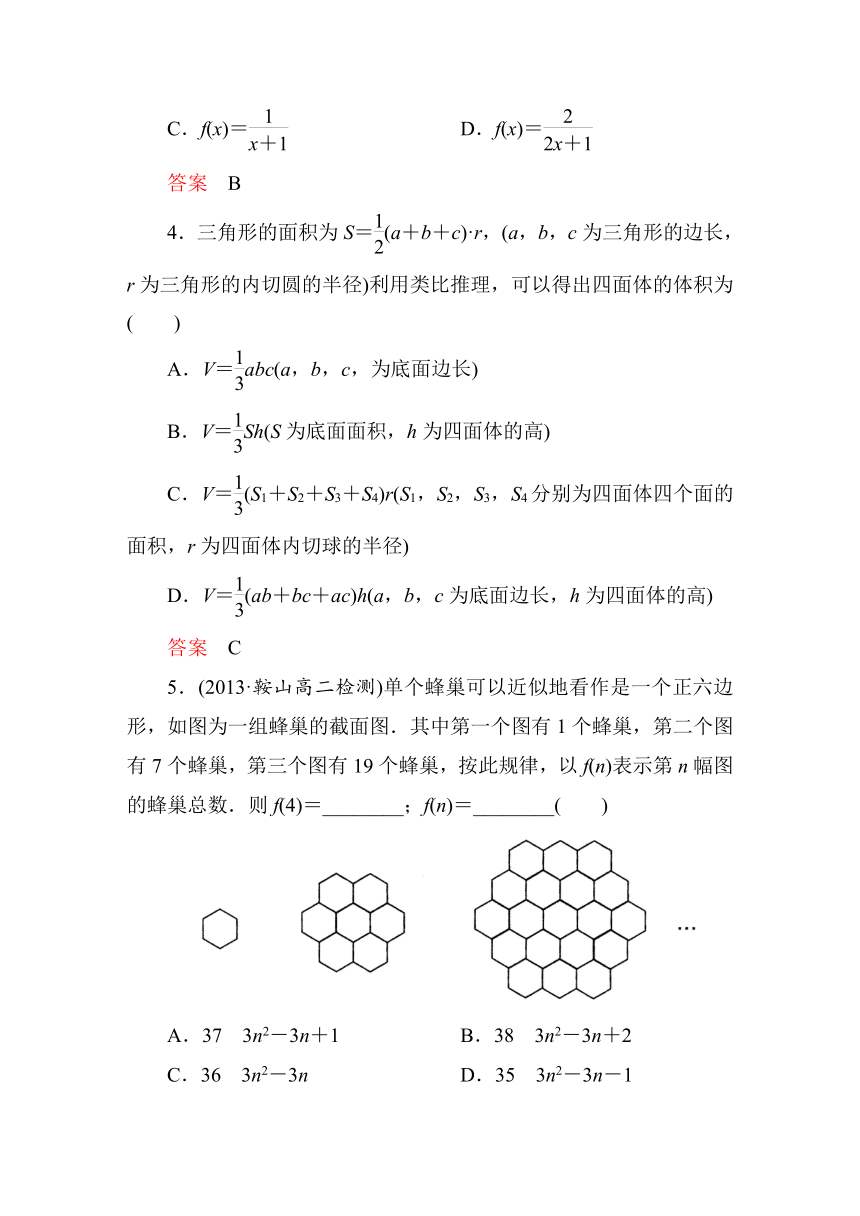
2.我们把1,4,9,16,25,…这些数称做正方形数,这是因为这些数目的点子可以排成一个正方形(如下图).试求第n个正方形数是( )
A.n(n-1) B.n(n+1)
C.n2 D.(n+1)2
答案 C
3.(2013·海口高二检测)已知f(x+1)=,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
答案 B
4.三角形的面积为S=(a+b+c)·r,(a,b,c为三角形的边长,r为三角形的内切圆的半径)利用类比推理,可以得出四面体的体积为( )
A.V=abc(a,b,c,为底面边长)
B.V=Sh(S为底面面积,h为四面体的高)
C.V=(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径)
D.V=(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高)
答案 C
5.(2013·鞍山高二检测)单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
A.37 3n2-3n+1 B.38 3n2-3n+2
C.36 3n2-3n D.35 3n2-3n-1
答案 A
6.用数学归纳法证明(n+1)(n+2)(n+3)·…·(n+n)=2n·1·3·…·(2n-1)(n∈N*)时,从n=k到n=k+1时左边需增乘的代数式是( )
A.2k+1 B.2(2k+1)
C. D.
答案 B
7.设M=(-1)(-1)(-1),且a+b+c=1(a,b,c均为正数),由综合法得M的取值范围是( )
A. B.
C.[1,8] D.[8,+∞)
答案 D
8.若x,y是正数,则(x+)2+(y+)2的最小值是( )
A.3 B.
C.4 D.
答案 C
9.设a,b,c∈(-∞,0),则a+,b+,a+( )
A.都不大于-2 B.都不小于-2
C.至少有一个不大于-2 D.至少有一个不小于-2
答案 D
解析 a++b++c+≤-6,三者不能都小于-2.故选D.
10.数列{an}中,若a1=,an=,(n≥2,n∈N),则a11的值为( )
A.-1 B.
C.1 D.2
答案 D
解析 a1=,a2=2,a3=-1,a4=,…三项为一个循环.
11.在平面直角坐标系内,方程+=1表示在x、y轴上的截距分别为a、b的直线,拓展到空间直角坐标系内,在x、y、z轴上的截距分别为a、b、c(abc≠0)的平面方程为( )
A.++=1 B.++=1
C.++=1 D.ax+by+cz=1
答案 A
12.若a1,a2,…,a8为各项都大于零的等差数列,公差d≠0,则( )
A.a1a8>a4a5 B.a1a8C.a1+a8>a4+a5 D.a1a8=a4a5
答案 B
解析 由a1+a8=a4+a5知道C不对,举例an=n,a1=1,a8=8,a4=4,a5=5,可知A、D不对.故选B.
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.观察下列不等式:1>,1++>1,1+++…+>,1+++…+>2,1+++…+>,…
由此猜测第n个不等式为________(n∈N*)
答案 1+++…+>(n∈N*)
解析 32=22-1,72=23-1,152=24-1,猜测1+++…+>.
14.由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=nt?m=n”类比得到“c≠0,a·c=b·c?a=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“=”类比得到=.以上的式子中,类比得到的结论正确的是________.
答案 ①②
15.f(n)=1+++…+(n∈N*),经计算得f(2)=,f(4)>2,f(8)>,f(16)>3,f(32)<,推测当n≥2时,有________.
答案 f(2n)>
解析 观察f(2),f(4),f(8),…可得.
16.若数列{an}的通项公式an=(n∈N*),记f(n)=(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________.
答案 f(n)=
解析 f(n)=…
=…
=×××××…××=.
三、解答题(本大题共6小题,共70分,解答应出写文字说明、证明过程或演算步骤)
17.(10分)已知x>0,y>0用分析法证明:(x2+y2)>(x3+y3).
证明 ∵x>0,y>0,
∴要证(x2+y2)>(x3+y3).
只要证(x2+y2)3>(x3+y3)2,
即证3x2+3y2>2xy.(*)
∵3x2+3y2-2xy=2(x2+y2)+(x-y)2>0,
∴(*)成立.故原不等式成立.
18.(12分)观察(1)tan10°tan20°+tan20°·tan60°+tan60°·tan10°=1;
(2)tan5°tan10°+tan10°tan75°+tan75°·tan5°=1.
由以上两式成立,推广到一般结论,写出你的推论.
解析 若α,β,γ都不是90°,且α+β+γ=90°,
则tanαtanβ+tanβtanγ+tanαtanγ=1.
19.(12分)已知f(x)=-x3-x+1,(x∈R)
求证:满足f(x)=0的实数值至多只有1个.
证明 ∵f′(x)=-3x2-1<0在x∈R上恒成立.
∴f(x)是R上的减函数.
假设f(x)=0的实数根x至少有二个,
不妨设x1≠x2且f(x1)=f(x2)=0.
∵y=f(x)在R单调递减,
∴当x1f(x2);
当x1>x2时,f(x1)这与f(x1)=f(x2)=0矛盾.
故假设不成立,所以f(x)=0至多只有一个实数根.
20.(12分)△ABC的三个内角A、B、C成等差数列,求证:+=.
解析 证明:要证原式,只要证+=3,
即+=1
即只要证=1,而A+C=2B,B=60°,b2=a2+c2-ac,
∴=
==1.
21.(12分)数列{an}的前n项和为Sn,若数列{an}的各项按如下规律排列:,,,,,,,,,,…,,…,…
(1)若数列{bn}满足b1=a1,b2=a2+a3,b3=a4+a5+a6,…,写出数列{bn}的前三项;
(2)猜想数列{bn}的通项并证明,并且求出{bn}的前n项和Tn.
解析 (1)b1=,b2=1,b3=.
(2)猜想bn=,依题意
bn===.
∵bn+1-bn=-=,
∴{bn}为公差的等差数列.
故Tn==.
22.(12分)已知函数f(x)=ax--2lnx,f(1)=0.
(1)若函数f(x)在其定义域内为单调函数,求实数a的取值范围?
(2)若函数f(x)的图像在x=1处的切线的斜率为0,且an+1=f′-nan+1,若a1≥3,求证:an≥n+2.
解析 (1)x>0,∵f(1)=a-b,∴a=b,f′(x)=a+-=a2+a-≠0.
①当a>0时,则有f′(x)=a2+a-≥0恒成立,即a-≥0,即a≥1.
②当a<0时,由x>0,知f′(x)<0恒成立.
③当a=0时,f′(x)=-,x>0,f′(x)<0恒成立.
∴若f(x)在定义域内为单调函数,
则a的取值范围是(-∞,0]∪[1,+∞).
(2)∵函数f(x)的图像在x=1处的切线斜率为0,
∴f′(1)=0,即a+a-2=0,解得a=1.
∴f′(x)=2,∴an+1=a-nan+1.
用数学归纳法证明:
①当n=1时,a1≥3=1+2,不等式成立;
②假设当n=k时,不等式成立,即ak≥k+2,
则ak-k≥2>0,∴ak+1=ak(ak-k)+1≥2(k+2)+1=(k+3)+k+2>k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2.
根据①②对于所有n≥1有an≥n+2.
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知扇形的孤长为l,半径为r,类比三角形的面积公式S=,可知扇形面积公式( )
A. B.
C. D.不可类比
答案 C
解析 可以将扇形看作曲边三角形,所以选C.
2.我们把1,4,9,16,25,…这些数称做正方形数,这是因为这些数目的点子可以排成一个正方形(如下图).试求第n个正方形数是( )
A.n(n-1) B.n(n+1)
C.n2 D.(n+1)2
答案 C
3.(2013·海口高二检测)已知f(x+1)=,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= B.f(x)=
C.f(x)= D.f(x)=
答案 B
4.三角形的面积为S=(a+b+c)·r,(a,b,c为三角形的边长,r为三角形的内切圆的半径)利用类比推理,可以得出四面体的体积为( )
A.V=abc(a,b,c,为底面边长)
B.V=Sh(S为底面面积,h为四面体的高)
C.V=(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径)
D.V=(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高)
答案 C
5.(2013·鞍山高二检测)单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
A.37 3n2-3n+1 B.38 3n2-3n+2
C.36 3n2-3n D.35 3n2-3n-1
答案 A
6.用数学归纳法证明(n+1)(n+2)(n+3)·…·(n+n)=2n·1·3·…·(2n-1)(n∈N*)时,从n=k到n=k+1时左边需增乘的代数式是( )
A.2k+1 B.2(2k+1)
C. D.
答案 B
7.设M=(-1)(-1)(-1),且a+b+c=1(a,b,c均为正数),由综合法得M的取值范围是( )
A. B.
C.[1,8] D.[8,+∞)
答案 D
8.若x,y是正数,则(x+)2+(y+)2的最小值是( )
A.3 B.
C.4 D.
答案 C
9.设a,b,c∈(-∞,0),则a+,b+,a+( )
A.都不大于-2 B.都不小于-2
C.至少有一个不大于-2 D.至少有一个不小于-2
答案 D
解析 a++b++c+≤-6,三者不能都小于-2.故选D.
10.数列{an}中,若a1=,an=,(n≥2,n∈N),则a11的值为( )
A.-1 B.
C.1 D.2
答案 D
解析 a1=,a2=2,a3=-1,a4=,…三项为一个循环.
11.在平面直角坐标系内,方程+=1表示在x、y轴上的截距分别为a、b的直线,拓展到空间直角坐标系内,在x、y、z轴上的截距分别为a、b、c(abc≠0)的平面方程为( )
A.++=1 B.++=1
C.++=1 D.ax+by+cz=1
答案 A
12.若a1,a2,…,a8为各项都大于零的等差数列,公差d≠0,则( )
A.a1a8>a4a5 B.a1a8
答案 B
解析 由a1+a8=a4+a5知道C不对,举例an=n,a1=1,a8=8,a4=4,a5=5,可知A、D不对.故选B.
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.观察下列不等式:1>,1++>1,1+++…+>,1+++…+>2,1+++…+>,…
由此猜测第n个不等式为________(n∈N*)
答案 1+++…+>(n∈N*)
解析 32=22-1,72=23-1,152=24-1,猜测1+++…+>.
14.由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=nt?m=n”类比得到“c≠0,a·c=b·c?a=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“=”类比得到=.以上的式子中,类比得到的结论正确的是________.
答案 ①②
15.f(n)=1+++…+(n∈N*),经计算得f(2)=,f(4)>2,f(8)>,f(16)>3,f(32)<,推测当n≥2时,有________.
答案 f(2n)>
解析 观察f(2),f(4),f(8),…可得.
16.若数列{an}的通项公式an=(n∈N*),记f(n)=(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________.
答案 f(n)=
解析 f(n)=…
=…
=×××××…××=.
三、解答题(本大题共6小题,共70分,解答应出写文字说明、证明过程或演算步骤)
17.(10分)已知x>0,y>0用分析法证明:(x2+y2)>(x3+y3).
证明 ∵x>0,y>0,
∴要证(x2+y2)>(x3+y3).
只要证(x2+y2)3>(x3+y3)2,
即证3x2+3y2>2xy.(*)
∵3x2+3y2-2xy=2(x2+y2)+(x-y)2>0,
∴(*)成立.故原不等式成立.
18.(12分)观察(1)tan10°tan20°+tan20°·tan60°+tan60°·tan10°=1;
(2)tan5°tan10°+tan10°tan75°+tan75°·tan5°=1.
由以上两式成立,推广到一般结论,写出你的推论.
解析 若α,β,γ都不是90°,且α+β+γ=90°,
则tanαtanβ+tanβtanγ+tanαtanγ=1.
19.(12分)已知f(x)=-x3-x+1,(x∈R)
求证:满足f(x)=0的实数值至多只有1个.
证明 ∵f′(x)=-3x2-1<0在x∈R上恒成立.
∴f(x)是R上的减函数.
假设f(x)=0的实数根x至少有二个,
不妨设x1≠x2且f(x1)=f(x2)=0.
∵y=f(x)在R单调递减,
∴当x1
当x1>x2时,f(x1)
故假设不成立,所以f(x)=0至多只有一个实数根.
20.(12分)△ABC的三个内角A、B、C成等差数列,求证:+=.
解析 证明:要证原式,只要证+=3,
即+=1
即只要证=1,而A+C=2B,B=60°,b2=a2+c2-ac,
∴=
==1.
21.(12分)数列{an}的前n项和为Sn,若数列{an}的各项按如下规律排列:,,,,,,,,,,…,,…,…
(1)若数列{bn}满足b1=a1,b2=a2+a3,b3=a4+a5+a6,…,写出数列{bn}的前三项;
(2)猜想数列{bn}的通项并证明,并且求出{bn}的前n项和Tn.
解析 (1)b1=,b2=1,b3=.
(2)猜想bn=,依题意
bn===.
∵bn+1-bn=-=,
∴{bn}为公差的等差数列.
故Tn==.
22.(12分)已知函数f(x)=ax--2lnx,f(1)=0.
(1)若函数f(x)在其定义域内为单调函数,求实数a的取值范围?
(2)若函数f(x)的图像在x=1处的切线的斜率为0,且an+1=f′-nan+1,若a1≥3,求证:an≥n+2.
解析 (1)x>0,∵f(1)=a-b,∴a=b,f′(x)=a+-=a2+a-≠0.
①当a>0时,则有f′(x)=a2+a-≥0恒成立,即a-≥0,即a≥1.
②当a<0时,由x>0,知f′(x)<0恒成立.
③当a=0时,f′(x)=-,x>0,f′(x)<0恒成立.
∴若f(x)在定义域内为单调函数,
则a的取值范围是(-∞,0]∪[1,+∞).
(2)∵函数f(x)的图像在x=1处的切线斜率为0,
∴f′(1)=0,即a+a-2=0,解得a=1.
∴f′(x)=2,∴an+1=a-nan+1.
用数学归纳法证明:
①当n=1时,a1≥3=1+2,不等式成立;
②假设当n=k时,不等式成立,即ak≥k+2,
则ak-k≥2>0,∴ak+1=ak(ak-k)+1≥2(k+2)+1=(k+3)+k+2>k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2.
根据①②对于所有n≥1有an≥n+2.
