5.6《扇形》(教学设计)-六年级上册数学人教版
文档属性
| 名称 | 5.6《扇形》(教学设计)-六年级上册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 13:23:42 | ||
图片预览


文档简介
《扇形》教学设计
备教材内容
1.本课时教学的是教材75页的内容及相关习题。
2.教材首先呈现了三个名称中含有“扇”字的物体,引出问题:什么是扇形?这样的引入方式,把“扇形”这个数学名词与学生已有的生活经验联系起来,有助于激发学生的学习兴趣。接着教材结合图示,以直接介绍的方式,揭示了“弧”“扇形”“圆心角”等术语的意义。最后明确扇形的大小与圆心角的大小紧密相关,也与它所在圆的半径的大小有关。
3.《数学课程标准》对扇形教学的要求是“知道”扇形,教学时可结合图示,逐一介绍这些基本概念。学生只要能看得懂、听得懂、讲得出,能在图上找得出相关对象,知道圆心角和半径都在变化时,扇形的大小也在随着变化就可以了。
备教法学法
学生已经掌握了圆的周长计算公式及圆的面积计算公式,积累了运用公式解决问题的经验。教师在此基础上,在自主探究的过程中,让学生通过观察、想象、分析和概括掌握扇形的特征,提高学生的思维能力及分析概括能力。
教学目标
1.认识扇形,掌握扇形的一些基本特征。体会扇形的大小和所在圆的半径、圆心角有关。
2.在观察、比较、分析、思考和讨论等活动中,知道扇形、弧和圆心角,初步学会画扇形的
基本方法,提高自主探索与合作交流的学习能力。
3.感受数学与生活的密切联系,增强数学的应用意识。
教学重难点
教学重点:掌握扇形的一些基本特征;体会扇形的大小和所在圆的半径、圆心角有关。
教学难点:体会扇形的大小和所在圆的半径、圆心角有关。
备已学知识
1.半径:连接圆心到圆上任意一点的线段。用字母r表示。
2.直径:通过圆心并且两端都在圆上的线段。用字母d表示。
3.圆的周长计算公式:C=2πr C=πd
4.圆的面积计算公式:S=πr2 S=π
S=π(C÷π÷2)2
备知识讲解
知识点 扇形的意义和画法
问题导入 欣赏图案。(教材75页)
过程讲解
1.弧的认识
(1)弧的意义:圆上任意两点之间的部分叫做弧。如图:
A、B两点之间的部分
(2)弧的读法:A、B两点之间的弧读作“弧AB”。
重点提示:弧是圆的一部分,是一段平滑的曲线。
(3)弧的写法:弧的符号是“⌒”,以点A、点B为端点的弧写作“AB”。
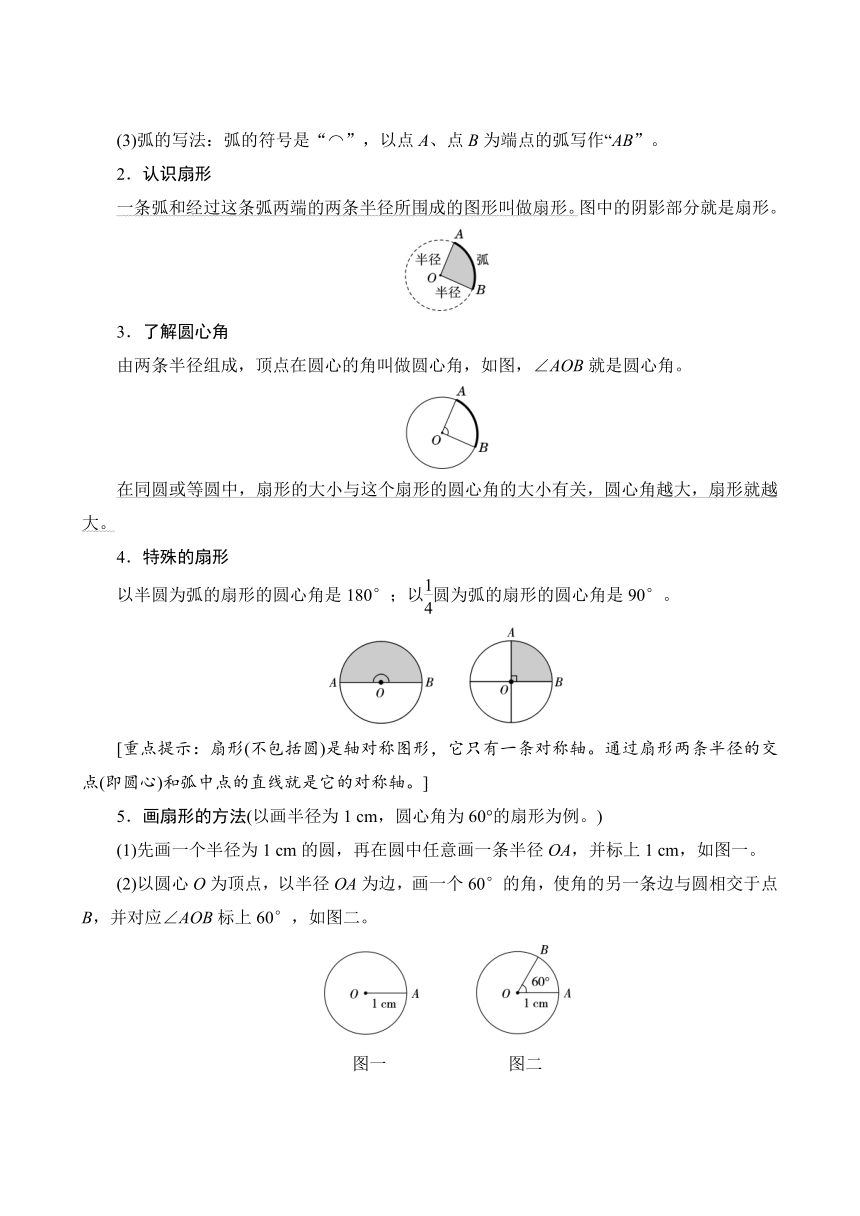
2.认识扇形
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中的阴影部分就是扇形。
3.了解圆心角
由两条半径组成,顶点在圆心的角叫做圆心角,如图,∠AOB就是圆心角。
在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
4.特殊的扇形
以半圆为弧的扇形的圆心角是180°;以圆为弧的扇形的圆心角是90°。
[重点提示:扇形(不包括圆)是轴对称图形,它只有一条对称轴。通过扇形两条半径的交点(即圆心)和弧中点的直线就是它的对称轴。]
5.画扇形的方法(以画半径为1 cm,圆心角为60°的扇形为例。)
(1)先画一个半径为1 cm的圆,再在圆中任意画一条半径OA,并标上1 cm,如图一。
(2)以圆心O为顶点,以半径OA为边,画一个60°的角,使角的另一条边与圆相交于点B,并对应∠AOB标上60°,如图二。
图一 图二
(3)弧AB和半径OA、OB所围成的图形就是一个圆心角为60°的扇形。
归纳总结
1.一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
2.画扇形的方法:(1)先画一个指定半径的圆,再在圆中任意画一条半径;(2)以圆心为顶点,以画好的半径为边,画一个指定度数的角,使角的另一条边与圆相交于一点。这两条半径与指定度数的圆心角所对应的弧围成的图形就是要画的扇形。
备易错易混
误区一 选择:下列图形中,(B)中的角是圆心角。
A. B. C. D.
错解分析 因为选项A、B、C中的角的顶点都不在圆心,两条边也不是半径,所以选项A、B、C中的角都不是圆心角。
错解改正 D
温馨提示
圆心角必须具备两个条件:一是顶点在圆心;二是角的两条边是圆的半径。
误区二 判断:圆心角越大,扇形越大。(√)
错解分析 此题错在没有说明是在同圆或等圆中。扇形的大小不仅与圆心角有关,还与所在圆的半径有关。
错解改正 ×
温馨提示
扇形的大小与圆心角有关,也与所在圆的半径有关。
备综合能力
综合运用 根据扇形和圆的关系解决实际问题
典型例题 已知圆的半径是5 cm,求图中扇形的周长。(得数保留整数。)
思路分析
正确解答
扇形的弧长:2×3.14×5÷360°×140°≈12(cm)
扇形的周长:12+5×2=22(cm)
答:图中扇形的周长大约是22 cm。
方法总结 1.扇形的弧长=扇形所在圆的周长÷360°×扇形圆心角的度数,字母公式为L弧=×n=πr。(n为扇形圆心角的度数。)
2.扇形的周长=扇形的弧长+半径×2,字母公式为C扇=πr+2r。(n为扇形圆心角的度数。)
思维开放 运用等腰直角三角形与扇形的特点解决问题
典型例题 右面是一个圆心角为45°的扇形,其中等腰直角三角形的斜边
长6 cm,求阴影部分的面积是多少平方厘米。
思路分析 观图可知:S阴影=S扇形-S等腰直角三角形
扇形所在圆的面积÷360°×扇形圆心角的度数
等腰直角三角形的面积是一个对角线长6 cm的正方形面积的一半,这个正方形的面积等于对角线长度的平方除以2,由此可以得出这个等腰直角三角形的面积=62÷2÷2。
正确解答
扇形的面积:×3.14×62=14.13(cm2)
等腰直角三角形的面积:62÷2÷2=9(cm2)
阴影部分的面积:14.13-9=5.13(cm2)
答:阴影部分的面积是5.13 cm2。
方法总结 扇形的面积=扇形所在圆的面积÷360°×扇形圆心角的度数,字母公式为
S扇=πr2。(n为扇形圆心角的度数。)
备教学资源
扇形和圆的关系
扇形指圆上两条半径和被半径所截的一段弧所围成的图形。因形状如一把扇子而得名。
圆也是扇形的一种,扇形的原始定义为“一圆中两半径与其弧所夹区域”,依理可以分成大弧与小弧两个,但表现时通常会指明弧的角度或者以图形显示。依此定义,全圆一般会被排除在扇形之外。因为全圆无法用两条半径表现,但是当我们以动态趋近的方式让一条半径向另一条半径靠近时,就可以得出全圆,而全圆的弧长、面积均与扇形一致,所以称全圆为扇形的一种并无错误。
简单地说,如果用“旋转角”的概念看扇形,全圆是扇形的一种,但如果用“图形角”来看,全圆就不会归纳在扇形的定义中。这不是“绝对定义”的问题,而是“角的概念”的推论问题。因此目前在小学阶段并不做这方面的深入探讨。
备教材内容
1.本课时教学的是教材75页的内容及相关习题。
2.教材首先呈现了三个名称中含有“扇”字的物体,引出问题:什么是扇形?这样的引入方式,把“扇形”这个数学名词与学生已有的生活经验联系起来,有助于激发学生的学习兴趣。接着教材结合图示,以直接介绍的方式,揭示了“弧”“扇形”“圆心角”等术语的意义。最后明确扇形的大小与圆心角的大小紧密相关,也与它所在圆的半径的大小有关。
3.《数学课程标准》对扇形教学的要求是“知道”扇形,教学时可结合图示,逐一介绍这些基本概念。学生只要能看得懂、听得懂、讲得出,能在图上找得出相关对象,知道圆心角和半径都在变化时,扇形的大小也在随着变化就可以了。
备教法学法
学生已经掌握了圆的周长计算公式及圆的面积计算公式,积累了运用公式解决问题的经验。教师在此基础上,在自主探究的过程中,让学生通过观察、想象、分析和概括掌握扇形的特征,提高学生的思维能力及分析概括能力。
教学目标
1.认识扇形,掌握扇形的一些基本特征。体会扇形的大小和所在圆的半径、圆心角有关。
2.在观察、比较、分析、思考和讨论等活动中,知道扇形、弧和圆心角,初步学会画扇形的
基本方法,提高自主探索与合作交流的学习能力。
3.感受数学与生活的密切联系,增强数学的应用意识。
教学重难点
教学重点:掌握扇形的一些基本特征;体会扇形的大小和所在圆的半径、圆心角有关。
教学难点:体会扇形的大小和所在圆的半径、圆心角有关。
备已学知识
1.半径:连接圆心到圆上任意一点的线段。用字母r表示。
2.直径:通过圆心并且两端都在圆上的线段。用字母d表示。
3.圆的周长计算公式:C=2πr C=πd
4.圆的面积计算公式:S=πr2 S=π
S=π(C÷π÷2)2
备知识讲解
知识点 扇形的意义和画法
问题导入 欣赏图案。(教材75页)
过程讲解
1.弧的认识
(1)弧的意义:圆上任意两点之间的部分叫做弧。如图:
A、B两点之间的部分
(2)弧的读法:A、B两点之间的弧读作“弧AB”。
重点提示:弧是圆的一部分,是一段平滑的曲线。
(3)弧的写法:弧的符号是“⌒”,以点A、点B为端点的弧写作“AB”。
2.认识扇形
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中的阴影部分就是扇形。
3.了解圆心角
由两条半径组成,顶点在圆心的角叫做圆心角,如图,∠AOB就是圆心角。
在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
4.特殊的扇形
以半圆为弧的扇形的圆心角是180°;以圆为弧的扇形的圆心角是90°。
[重点提示:扇形(不包括圆)是轴对称图形,它只有一条对称轴。通过扇形两条半径的交点(即圆心)和弧中点的直线就是它的对称轴。]
5.画扇形的方法(以画半径为1 cm,圆心角为60°的扇形为例。)
(1)先画一个半径为1 cm的圆,再在圆中任意画一条半径OA,并标上1 cm,如图一。
(2)以圆心O为顶点,以半径OA为边,画一个60°的角,使角的另一条边与圆相交于点B,并对应∠AOB标上60°,如图二。
图一 图二
(3)弧AB和半径OA、OB所围成的图形就是一个圆心角为60°的扇形。
归纳总结
1.一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
2.画扇形的方法:(1)先画一个指定半径的圆,再在圆中任意画一条半径;(2)以圆心为顶点,以画好的半径为边,画一个指定度数的角,使角的另一条边与圆相交于一点。这两条半径与指定度数的圆心角所对应的弧围成的图形就是要画的扇形。
备易错易混
误区一 选择:下列图形中,(B)中的角是圆心角。
A. B. C. D.
错解分析 因为选项A、B、C中的角的顶点都不在圆心,两条边也不是半径,所以选项A、B、C中的角都不是圆心角。
错解改正 D
温馨提示
圆心角必须具备两个条件:一是顶点在圆心;二是角的两条边是圆的半径。
误区二 判断:圆心角越大,扇形越大。(√)
错解分析 此题错在没有说明是在同圆或等圆中。扇形的大小不仅与圆心角有关,还与所在圆的半径有关。
错解改正 ×
温馨提示
扇形的大小与圆心角有关,也与所在圆的半径有关。
备综合能力
综合运用 根据扇形和圆的关系解决实际问题
典型例题 已知圆的半径是5 cm,求图中扇形的周长。(得数保留整数。)
思路分析
正确解答
扇形的弧长:2×3.14×5÷360°×140°≈12(cm)
扇形的周长:12+5×2=22(cm)
答:图中扇形的周长大约是22 cm。
方法总结 1.扇形的弧长=扇形所在圆的周长÷360°×扇形圆心角的度数,字母公式为L弧=×n=πr。(n为扇形圆心角的度数。)
2.扇形的周长=扇形的弧长+半径×2,字母公式为C扇=πr+2r。(n为扇形圆心角的度数。)
思维开放 运用等腰直角三角形与扇形的特点解决问题
典型例题 右面是一个圆心角为45°的扇形,其中等腰直角三角形的斜边
长6 cm,求阴影部分的面积是多少平方厘米。
思路分析 观图可知:S阴影=S扇形-S等腰直角三角形
扇形所在圆的面积÷360°×扇形圆心角的度数
等腰直角三角形的面积是一个对角线长6 cm的正方形面积的一半,这个正方形的面积等于对角线长度的平方除以2,由此可以得出这个等腰直角三角形的面积=62÷2÷2。
正确解答
扇形的面积:×3.14×62=14.13(cm2)
等腰直角三角形的面积:62÷2÷2=9(cm2)
阴影部分的面积:14.13-9=5.13(cm2)
答:阴影部分的面积是5.13 cm2。
方法总结 扇形的面积=扇形所在圆的面积÷360°×扇形圆心角的度数,字母公式为
S扇=πr2。(n为扇形圆心角的度数。)
备教学资源
扇形和圆的关系
扇形指圆上两条半径和被半径所截的一段弧所围成的图形。因形状如一把扇子而得名。
圆也是扇形的一种,扇形的原始定义为“一圆中两半径与其弧所夹区域”,依理可以分成大弧与小弧两个,但表现时通常会指明弧的角度或者以图形显示。依此定义,全圆一般会被排除在扇形之外。因为全圆无法用两条半径表现,但是当我们以动态趋近的方式让一条半径向另一条半径靠近时,就可以得出全圆,而全圆的弧长、面积均与扇形一致,所以称全圆为扇形的一种并无错误。
简单地说,如果用“旋转角”的概念看扇形,全圆是扇形的一种,但如果用“图形角”来看,全圆就不会归纳在扇形的定义中。这不是“绝对定义”的问题,而是“角的概念”的推论问题。因此目前在小学阶段并不做这方面的深入探讨。
