5.3《圆的面积》(教案)-六年级上册数学人教版
文档属性
| 名称 | 5.3《圆的面积》(教案)-六年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 659.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 13:26:20 | ||
图片预览


文档简介
《圆的面积》教学设计
备教材内容
1.本课时学习的是教材67~68页的内容及相关习题。
2.本课时教学圆的面积。教材首先通过求圆形草坪的占地面积提出“怎样计算一个圆的面积呢?”这个问题,引出圆的面积的概念。然后指导学生用学具进行操作,通过分割、拼组的方法推导出圆的面积计算公式,体会转化和极限思想。例1是应用圆的面积计算公式解决问题。
3.这部分内容是在学生学习了多边形面积的概念及多边形的面积计算方法的基础上进行教学的,同时也为后面学习扇形、圆柱、圆锥打下基础。
备教法学法
学生已经掌握了长方形、平行四边形、三角形和梯形的面积计算公式及推导方法,积累了解决这类问题的经验,教师教学时可以通过剪拼、推导、讨论和归纳等活动,培养学生的动手操作能力、逻辑推理能力和综合分析能力,发展空间观念,渗透转化和极限思想。
教学目标
1.理解和掌握圆的面积计算公式。
2.经历实验操作、观察发现、逻辑推理、归纳概括的过程,积累数学活动经验,体会转化、
推理、极限等数学思想方法,发展逻辑推理能力。
3.通过解决问题激发探索精神,提升学习兴趣。
教学重难点
教学重点:
理解和掌握圆的面积计算公式。
教学难点:
利用多种方法推导圆的面积计算公式。
备已学知识
1.面积:指的是物体表面或围成的平面图形的大小。
2.长方形的面积计算公式:S=ab。
3.平行四边形的面积计算公式:S=ah。
4.三角形的面积计算公式:S=ah÷2。
5.梯形的面积计算公式:S=(a+b)h÷2。
备知识讲解
知识点一 圆的面积的意义
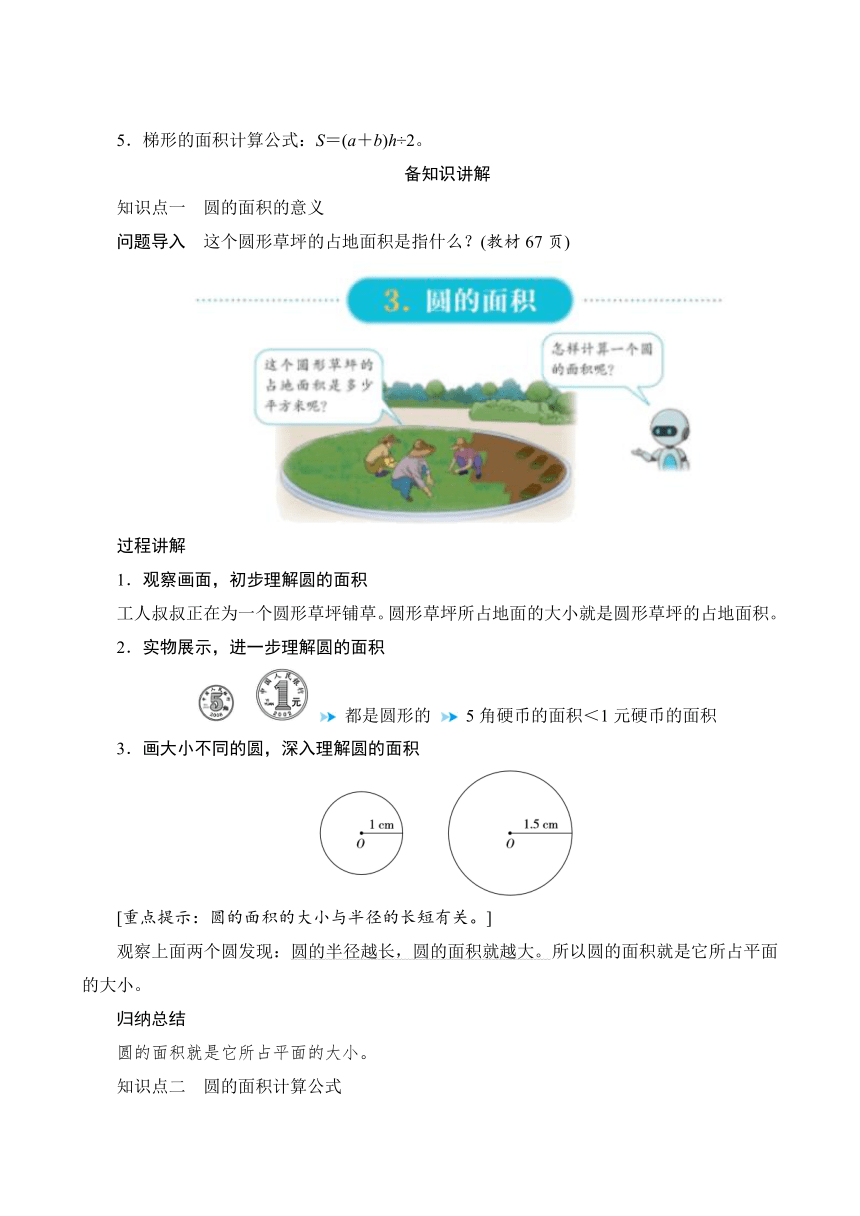
问题导入 这个圆形草坪的占地面积是指什么?(教材67页)
过程讲解
1.观察画面,初步理解圆的面积
工人叔叔正在为一个圆形草坪铺草。圆形草坪所占地面的大小就是圆形草坪的占地面积。
2.实物展示,进一步理解圆的面积
都是圆形的 5角硬币的面积<1元硬币的面积
3.画大小不同的圆,深入理解圆的面积
[重点提示:圆的面积的大小与半径的长短有关。]
观察上面两个圆发现:圆的半径越长,圆的面积就越大。所以圆的面积就是它所占平面的大小。
归纳总结
圆的面积就是它所占平面的大小。
知识点二 圆的面积计算公式
问题导入 怎样计算一个圆的面积呢?(教材67页)
过程讲解
1.探究测量圆的面积的方法
圆是曲线图形,用以1 cm2、1 dm2或1 m2为面积单位的正方形不能直接测量出它的面积,但是可以运用剪拼法把圆转化成学过的图形,推导出圆的面积计算公式。
2.转化方法
在硬纸上画一个圆,把圆分成若干(偶数)等份,剪开后,用这些近似于等腰三角形的小纸片拼成学过的图形。
3.推导圆的面积计算公式
(1)转化方法演示。
[思想方法解读:把圆平均分的份数越多,拼成的图形就越接近于长方形,这体现了极限思想。所谓极限思想是指用极限的概念分析和解决问题的一种数学思想。]
发现:把圆平均分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
(2)探究拼成的近似的长方形的长和宽分别与圆的周长和半径之间的关系。
思想方法提示 把圆的面积转化成长方形的面积体现了转化思想。
(3)推导圆的面积计算公式。
因为长方形的面积=长×宽,所以圆的面积=圆的周长的一半×圆的半径。如果用S表示圆的面积,那么圆的面积计算公式就是S=πr2。
归纳总结
圆的面积计算公式:S=πr2。
拓展提高
1.把圆转化成三角形或者梯形,都可以推导出圆的面积计算公式,转化方法如下:
2.如果一个圆的半径(直径或周长)扩大到原来的n倍,那么这个圆的面积就扩大到原来的n2倍;如果一个圆的半径(直径或周长)缩小到原来的,那么这个圆的面积就缩小到原来的。
知识点三 圆的面积计算公式的应用
应用一 已知圆的半径,求圆的面积。
典型例题 一个圆形花坛的半径是3 m,它的面积是多少平方米?
思路分析 已知圆形花坛的半径,可以直接应用圆的面积计算公式计算。
正确解答 3.14×32=28.26(m2)
答:它的面积是28.26 m2。
应用二 已知圆的直径,求圆的面积。
典型例题 圆形草坪的直径是20 m,每平方米草皮8元。铺满草皮需要多少钱?(教材68页例1)
思路分析
正确解答 3.14×(20÷2)2=314(m2) 314×8=2512(元)
答:铺满草皮需要2512元。
应用三 已知圆的周长,求圆的面积。
典型例题 一个圆形蓄水池的周长是25.12 m,它的占地面积是多少平方米?
思路分析 已知这个圆形蓄水池的周长,求它的占地面积,可以先求出这个圆形蓄水池的半径,再应用圆的面积计算公式计算。
正确解答 3.14×(25.12÷3.14÷2)2=3.14×42=50.24(m2)
答:它的占地面积是50.24 m2。
方法总结 已知圆的直径求圆的面积:S=π;已知圆的周长求圆的面积:
S=π。
备易错易混
误区一 一颗圆形纽扣的半径是1.5 cm,它正面的面积是多少?
3.14×1.52=3.14×3=9.42(cm2)
答:它正面的面积是9.42 cm2。
错解分析 此题错在计算1.52时,把1.52当成1.5×2计算了,1.52表示的是1.5×1.5。
错解改正
3.14×1.52=3.14×2.25=7.065(cm2)
答:它正面的面积是7.065 cm2。
温馨提示
在计算圆的面积时,不要把r2当成r×2计算,r2表示的是r×r。
误区二 选择:在边长是8 cm的正方形里画一个最大的圆,圆的面积是(A)cm2。
A.64π B.16π C.8π
错解分析 在正方形里画一个最大的圆,这个圆的直径应该等于正方形的边长,如下图所示:
已知圆的直径求圆的面积,根据公式S=π,可以求出这个圆的面积,即S=π=16π(cm2)。
错解改正 B
温馨提示
已知圆的直径求圆的面积,计算公式是S=π。
备综合能力
思维开放 运用割补法解决求不规则图形的面积的问题
典型例题 如右图,OA、OB分别是小半圆的直径,且OA=OB=6 cm,
∠AOB=90°,阴影部分的面积是多少平方厘米?
思路分析 图中阴影部分的形状不规则,将阴影部分进行割补,使其变成规则图形,如下图所示:
由图可知:阴影部分的面积=大圆的面积-三角形AOB的面积。
正确解答
3.14×62×-6×6×
=28.26-18
=10.26(cm2)
答:阴影部分的面积是10.26 cm2。
方法提示 运用割补法把阴影部分的面积转化成“S大圆-S三角形AOB”是解决此题的关键。
方法运用 运用转化法解决求不规则图形的面积的问题
典型例题 求下图中阴影部分的面积。(单位:cm)
思路分析 把左下角的圆沿着长方形下面的边向右平移12 cm,与右上角的阴影部分相接,使阴影部分转化成规则图形,如下图所示:(单位:cm)
平移,F
由上图可知:求阴影部分的面积就是求边长是12 cm的正方形的面积。
正确解答 12×12=144(cm2)
答:阴影部分的面积是144 cm2。
方法总结 在求不规则图形的面积时,可以先将其中的部分图形进行平移或旋转,使其转化成规则图形,再进行计算。
备教学资源
割圆术
中国魏晋时期数学家刘徽在《九章算术》圆田术注中首创了用无穷小分割方法和极限思想证明圆的面积公式,进而求圆周率的近似值的方法。《九章算术》方田章提出了圆的面积计算公式“半周半径相乘得积步”,即S=,其中S、L、r分别表示圆的面积、周长、半径。刘徽从圆内接正六边形起割圆,到正12,24,…边形,它们的面积与圆相比都有缺失,然而“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。因而刘徽肯定了圆面积的一个上界序列的极限就是该圆的面积。最后,刘徽将与圆周合体的正多边形“觚而裁之”,即分割成无穷多个小等腰三角形,求这无穷多个小等腰三角形的面积之和,便证明了《九章算术》中圆的面积公式。刘徽批评了人们长期沿袭“周三径一”的错误,从而在中国首创了求圆周率的近似值的方法。他从直径为2尺的圆开始割圆,利用勾股定理,依次求出正多边形的边心距、边长和面积,取314平方寸为圆面积的近似值,将其代入圆的面积公式S=中,求出圆周长的近似值为62寸8分。再将其与直径20寸相约,便得到圆周率,相当于π=3.14。刘徽还求出圆周率为,相当于π=3.1416。后来,南北朝时期的祖冲之更进一步将圆周率的值精确到8位有效数字,并确定π=为密率。这些成就在世界上领先约千年。1427年卡西的值超过了8位有效数字,16世纪末德国的奥托、荷兰的安托尼兹先后提出了π=。
备教材内容
1.本课时学习的是教材67~68页的内容及相关习题。
2.本课时教学圆的面积。教材首先通过求圆形草坪的占地面积提出“怎样计算一个圆的面积呢?”这个问题,引出圆的面积的概念。然后指导学生用学具进行操作,通过分割、拼组的方法推导出圆的面积计算公式,体会转化和极限思想。例1是应用圆的面积计算公式解决问题。
3.这部分内容是在学生学习了多边形面积的概念及多边形的面积计算方法的基础上进行教学的,同时也为后面学习扇形、圆柱、圆锥打下基础。
备教法学法
学生已经掌握了长方形、平行四边形、三角形和梯形的面积计算公式及推导方法,积累了解决这类问题的经验,教师教学时可以通过剪拼、推导、讨论和归纳等活动,培养学生的动手操作能力、逻辑推理能力和综合分析能力,发展空间观念,渗透转化和极限思想。
教学目标
1.理解和掌握圆的面积计算公式。
2.经历实验操作、观察发现、逻辑推理、归纳概括的过程,积累数学活动经验,体会转化、
推理、极限等数学思想方法,发展逻辑推理能力。
3.通过解决问题激发探索精神,提升学习兴趣。
教学重难点
教学重点:
理解和掌握圆的面积计算公式。
教学难点:
利用多种方法推导圆的面积计算公式。
备已学知识
1.面积:指的是物体表面或围成的平面图形的大小。
2.长方形的面积计算公式:S=ab。
3.平行四边形的面积计算公式:S=ah。
4.三角形的面积计算公式:S=ah÷2。
5.梯形的面积计算公式:S=(a+b)h÷2。
备知识讲解
知识点一 圆的面积的意义
问题导入 这个圆形草坪的占地面积是指什么?(教材67页)
过程讲解
1.观察画面,初步理解圆的面积
工人叔叔正在为一个圆形草坪铺草。圆形草坪所占地面的大小就是圆形草坪的占地面积。
2.实物展示,进一步理解圆的面积
都是圆形的 5角硬币的面积<1元硬币的面积
3.画大小不同的圆,深入理解圆的面积
[重点提示:圆的面积的大小与半径的长短有关。]
观察上面两个圆发现:圆的半径越长,圆的面积就越大。所以圆的面积就是它所占平面的大小。
归纳总结
圆的面积就是它所占平面的大小。
知识点二 圆的面积计算公式
问题导入 怎样计算一个圆的面积呢?(教材67页)
过程讲解
1.探究测量圆的面积的方法
圆是曲线图形,用以1 cm2、1 dm2或1 m2为面积单位的正方形不能直接测量出它的面积,但是可以运用剪拼法把圆转化成学过的图形,推导出圆的面积计算公式。
2.转化方法
在硬纸上画一个圆,把圆分成若干(偶数)等份,剪开后,用这些近似于等腰三角形的小纸片拼成学过的图形。
3.推导圆的面积计算公式
(1)转化方法演示。
[思想方法解读:把圆平均分的份数越多,拼成的图形就越接近于长方形,这体现了极限思想。所谓极限思想是指用极限的概念分析和解决问题的一种数学思想。]
发现:把圆平均分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
(2)探究拼成的近似的长方形的长和宽分别与圆的周长和半径之间的关系。
思想方法提示 把圆的面积转化成长方形的面积体现了转化思想。
(3)推导圆的面积计算公式。
因为长方形的面积=长×宽,所以圆的面积=圆的周长的一半×圆的半径。如果用S表示圆的面积,那么圆的面积计算公式就是S=πr2。
归纳总结
圆的面积计算公式:S=πr2。
拓展提高
1.把圆转化成三角形或者梯形,都可以推导出圆的面积计算公式,转化方法如下:
2.如果一个圆的半径(直径或周长)扩大到原来的n倍,那么这个圆的面积就扩大到原来的n2倍;如果一个圆的半径(直径或周长)缩小到原来的,那么这个圆的面积就缩小到原来的。
知识点三 圆的面积计算公式的应用
应用一 已知圆的半径,求圆的面积。
典型例题 一个圆形花坛的半径是3 m,它的面积是多少平方米?
思路分析 已知圆形花坛的半径,可以直接应用圆的面积计算公式计算。
正确解答 3.14×32=28.26(m2)
答:它的面积是28.26 m2。
应用二 已知圆的直径,求圆的面积。
典型例题 圆形草坪的直径是20 m,每平方米草皮8元。铺满草皮需要多少钱?(教材68页例1)
思路分析
正确解答 3.14×(20÷2)2=314(m2) 314×8=2512(元)
答:铺满草皮需要2512元。
应用三 已知圆的周长,求圆的面积。
典型例题 一个圆形蓄水池的周长是25.12 m,它的占地面积是多少平方米?
思路分析 已知这个圆形蓄水池的周长,求它的占地面积,可以先求出这个圆形蓄水池的半径,再应用圆的面积计算公式计算。
正确解答 3.14×(25.12÷3.14÷2)2=3.14×42=50.24(m2)
答:它的占地面积是50.24 m2。
方法总结 已知圆的直径求圆的面积:S=π;已知圆的周长求圆的面积:
S=π。
备易错易混
误区一 一颗圆形纽扣的半径是1.5 cm,它正面的面积是多少?
3.14×1.52=3.14×3=9.42(cm2)
答:它正面的面积是9.42 cm2。
错解分析 此题错在计算1.52时,把1.52当成1.5×2计算了,1.52表示的是1.5×1.5。
错解改正
3.14×1.52=3.14×2.25=7.065(cm2)
答:它正面的面积是7.065 cm2。
温馨提示
在计算圆的面积时,不要把r2当成r×2计算,r2表示的是r×r。
误区二 选择:在边长是8 cm的正方形里画一个最大的圆,圆的面积是(A)cm2。
A.64π B.16π C.8π
错解分析 在正方形里画一个最大的圆,这个圆的直径应该等于正方形的边长,如下图所示:
已知圆的直径求圆的面积,根据公式S=π,可以求出这个圆的面积,即S=π=16π(cm2)。
错解改正 B
温馨提示
已知圆的直径求圆的面积,计算公式是S=π。
备综合能力
思维开放 运用割补法解决求不规则图形的面积的问题
典型例题 如右图,OA、OB分别是小半圆的直径,且OA=OB=6 cm,
∠AOB=90°,阴影部分的面积是多少平方厘米?
思路分析 图中阴影部分的形状不规则,将阴影部分进行割补,使其变成规则图形,如下图所示:
由图可知:阴影部分的面积=大圆的面积-三角形AOB的面积。
正确解答
3.14×62×-6×6×
=28.26-18
=10.26(cm2)
答:阴影部分的面积是10.26 cm2。
方法提示 运用割补法把阴影部分的面积转化成“S大圆-S三角形AOB”是解决此题的关键。
方法运用 运用转化法解决求不规则图形的面积的问题
典型例题 求下图中阴影部分的面积。(单位:cm)
思路分析 把左下角的圆沿着长方形下面的边向右平移12 cm,与右上角的阴影部分相接,使阴影部分转化成规则图形,如下图所示:(单位:cm)
平移,F
由上图可知:求阴影部分的面积就是求边长是12 cm的正方形的面积。
正确解答 12×12=144(cm2)
答:阴影部分的面积是144 cm2。
方法总结 在求不规则图形的面积时,可以先将其中的部分图形进行平移或旋转,使其转化成规则图形,再进行计算。
备教学资源
割圆术
中国魏晋时期数学家刘徽在《九章算术》圆田术注中首创了用无穷小分割方法和极限思想证明圆的面积公式,进而求圆周率的近似值的方法。《九章算术》方田章提出了圆的面积计算公式“半周半径相乘得积步”,即S=,其中S、L、r分别表示圆的面积、周长、半径。刘徽从圆内接正六边形起割圆,到正12,24,…边形,它们的面积与圆相比都有缺失,然而“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。因而刘徽肯定了圆面积的一个上界序列的极限就是该圆的面积。最后,刘徽将与圆周合体的正多边形“觚而裁之”,即分割成无穷多个小等腰三角形,求这无穷多个小等腰三角形的面积之和,便证明了《九章算术》中圆的面积公式。刘徽批评了人们长期沿袭“周三径一”的错误,从而在中国首创了求圆周率的近似值的方法。他从直径为2尺的圆开始割圆,利用勾股定理,依次求出正多边形的边心距、边长和面积,取314平方寸为圆面积的近似值,将其代入圆的面积公式S=中,求出圆周长的近似值为62寸8分。再将其与直径20寸相约,便得到圆周率,相当于π=3.14。刘徽还求出圆周率为,相当于π=3.1416。后来,南北朝时期的祖冲之更进一步将圆周率的值精确到8位有效数字,并确定π=为密率。这些成就在世界上领先约千年。1427年卡西的值超过了8位有效数字,16世纪末德国的奥托、荷兰的安托尼兹先后提出了π=。
