5.2《圆的周长》(教学设计)-六年级上册数学人教版
文档属性
| 名称 | 5.2《圆的周长》(教学设计)-六年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 643.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 13:28:59 | ||
图片预览



文档简介
《圆的周长》教学设计
备教材内容
1.本课时学习的是教材62~64页的内容及相关习题。
2.教材首先从实际情境入手,通过让学生思考情境图中的问题引出圆的周长的概念。接着引导学生用不同的方法测量,自主发现圆的周长和直径的比值是一个固定值,从而引出圆周率的概念,并总结出圆的周长计算公式。例1是一个与圆的周长计算有关的实际问题,通过学生经常看到或使用的自行车引出问题,能让学生体会到数学知识的广泛应用。
3.这部分内容是在学生学习了周长的一般概念以及长方形、正方形的周长计算公式,并初步认识了圆的基础上进行教学的。它是学生初步研究曲线图形的开始,也是后面学习圆的面积以及圆柱、圆锥等知识的基础,是小学几何知识中的一项重要内容。
备教法学法
学生已经掌握长方形、正方形的周长计算公式,教师在此基础上先引导学生通过摸一摸、动手操作、猜想验证等活动,使学生经历整个探究知识的过程。再通过对圆周率的探究,培养学生主动探究的精神,提高动手操作能力和逻辑思维能力。最后引导学生推导圆的周长计算公式,提高学生的比较、分析能力,体会转化思想。
教学目标
1.理解圆周长的概念及圆周率的意义,掌握圆周长的计算公式。
2.经历操作、猜想、探究的学习活动,体会“化曲为直”的转化思想,积累数学活动经验。
3.了解数学文化,提高学习兴趣。
教学重难点
教学重点:
理解圆周率的意义,掌握圆周长的计算公式。
教学难点:
理解圆周率的意义。
备已学知识
1.周长:封闭图形一周的长度。
2.长方形(正方形)的周长:围成长方形(正方形)的四条边的长度和。
3.长方形的周长计算公式:C=(a+b)×2。
4.正方形的周长计算公式:C=4a。
备知识讲解
知识点一 圆的周长的意义及测量方法
问题导入 圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。(教材62页)
过程讲解
1.理解圆的周长的意义
2.圆的周长的测量方法
(1)滚动法。
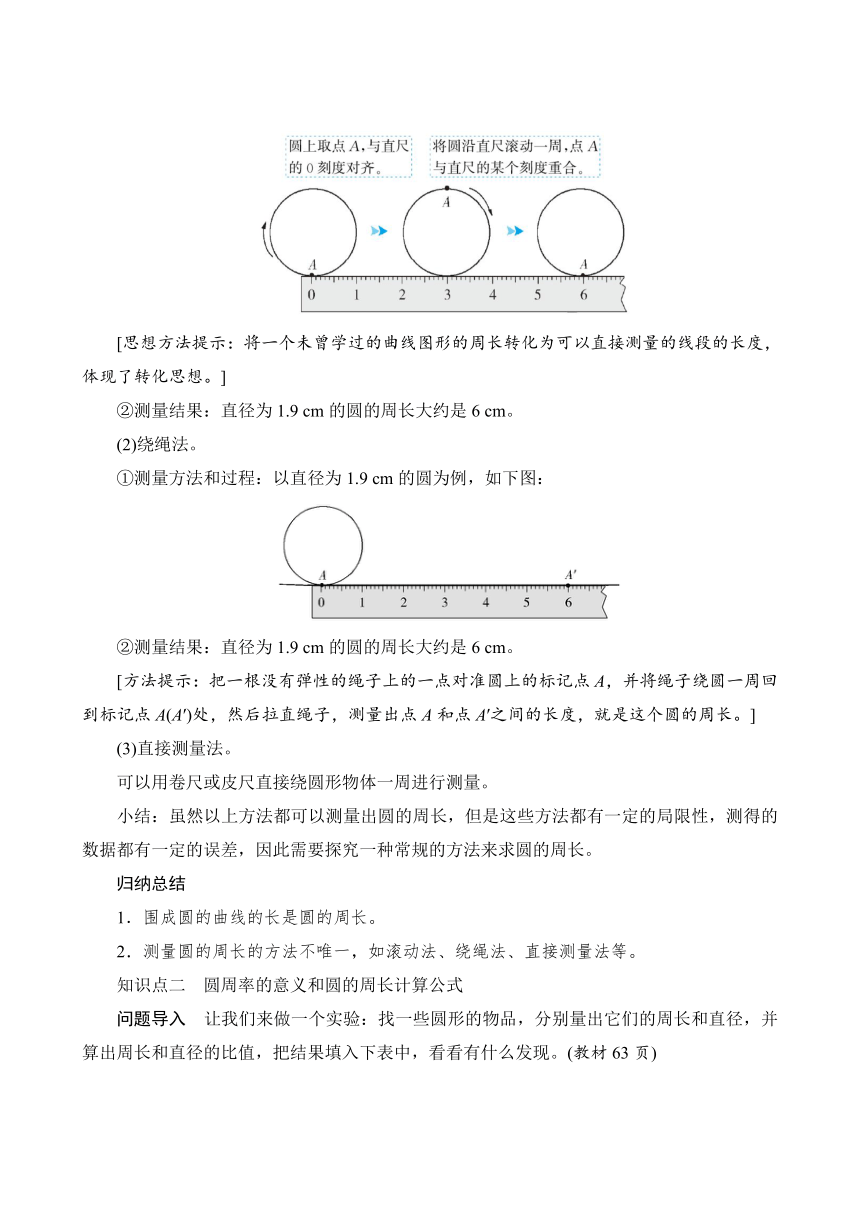
①测量方法和过程:以直径为1.9 cm的圆为例,如下图:
[思想方法提示:将一个未曾学过的曲线图形的周长转化为可以直接测量的线段的长度,体现了转化思想。]
②测量结果:直径为1.9 cm的圆的周长大约是6 cm。
(2)绕绳法。
①测量方法和过程:以直径为1.9 cm的圆为例,如下图:
②测量结果:直径为1.9 cm的圆的周长大约是6 cm。
[方法提示:把一根没有弹性的绳子上的一点对准圆上的标记点A,并将绳子绕圆一周回到标记点A(A′)处,然后拉直绳子,测量出点A和点A′之间的长度,就是这个圆的周长。]
(3)直接测量法。
可以用卷尺或皮尺直接绕圆形物体一周进行测量。
小结:虽然以上方法都可以测量出圆的周长,但是这些方法都有一定的局限性,测得的数据都有一定的误差,因此需要探究一种常规的方法来求圆的周长。
归纳总结
1.围成圆的曲线的长是圆的周长。
2.测量圆的周长的方法不唯一,如滚动法、绕绳法、直接测量法等。
知识点二 圆周率的意义和圆的周长计算公式
问题导入 让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中,看看有什么发现。(教材63页)
物品名称 周长 直径 的比值 (保留两位小数)
过程讲解
1.选择物品,测量数据并完成表格
任意选择4个不同的圆形物品,分别测量出它们的直径和周长,并计算出周长和直径的比值,完成表格。(以编者测量的数据为例。)
物品名称 周长 直径 的比值 (保留两位小数)
圆形学具 6 cm 1.9 cm 3.16
圆形纸片 31.5 cm 10 cm 3.15
圆形瓶盖 10 cm 3.2 cm 3.13
圆形碗的碗口 34.5 cm 11 cm 3.14
2.观察并对比数据,找出规律
直径:11 cm>10 cm>3.2 cm>1.9 cm
周长:34.5 cm>31.5 cm>10 cm>6 cm
规律:圆的周长与它的直径有关,直径越长,周长越长。
3.观察表格中圆的周长和直径的比值,发现圆的周长与直径的关系
圆的周长和直径的比值:3.16、3.15、3.13、3.14。
发现:一个圆的周长总是它的直径的3倍多一些。
4.理解圆周率的意义
教育视点 我国数学家祖冲之是世界上第一个把圆周率的值精确到7位小数的人。
因为测量时存在一定的误差,所以这几个圆形物品的周长和直径的比值不相等。实际上这个比值是一个固定的数,我们把它叫做圆周率 。
圆周率是任意一个圆的周长与它的直径的比值,这个比值是一个固定的数,用字母π(pài)表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
[德育建议:引导学生经历动手操作、自主探究圆周率的过程,理解圆周率的意义,培养严谨认真的思维习惯。同时通过了解中国伟大的数学家祖冲之在圆周率方面的巨大贡献,感受古代人民非凡的智慧,激发学生的爱国情感。]
5.根据圆的周长与直径的关系推导圆的周长计算公式
(1)=圆周率 圆的周长=直径×圆周率
(2)
圆的周长=半径×2×圆周率
归纳总结
1.
π=3.1415926535……
2.圆的周长=直径×圆周率或圆的周长=半径×2×圆周率。如果用C表示圆的周长,用r表示圆的半径,用d表示圆的直径,那么圆的周长计算公式是C=πd或C=2πr。
拓展提高
1.圆的周长与它的半径、直径的关系:(1)圆的半径或直径扩大到原来的几倍,它的周长也扩大到原来的几倍。(2)圆的半径或直径缩小到原来的几分之一,它的周长也缩小到原来的几分之一。
2.半圆的周长和圆的周长的一半。
知识点三 圆的周长计算公式的应用
应用一 已知圆的半径,求圆的周长。
典型例题 一辆自行车轮子的半径大约是33 cm。这辆自行车轮子转1圈,大约可以走多远?(结果保留整米数。)小明家离学校1 km,骑车从家到学校,轮子大约转了多少圈?(教材64页例1)
思路分析 求这辆自行车轮子转1圈,大约可以走多远,就是求这辆自行车轮子的周长。自行车轮子是圆形的,已知它的半径,可以直接应用公式C=2πr求出它的周长。
因为小明家离学校1 km,所以求小明骑车从家到学校,轮子大约转了多少圈,就是求1 km里面大约有多少个自行车轮子的周长,即用1 km除以自行车轮子的周长。
正确解答
2×3.14×33=207.24(cm)≈2(m) 1 km=1000 m 1000÷2=500(圈)
答:这辆自行车轮子转1圈,大约可以走2 m。骑车从家到学校,轮子大约转了500圈。
应用二 已知圆的直径,求圆的周长。
典型例题 一个圆形花坛的直径是20 m,它的周长是多少米?
思路分析 已知圆形花坛的直径,可以直接应用公式C=πd求出它的周长。
正确解答 3.14×20=62.8(m)
答:它的周长是62.8 m。
应用三 已知圆的周长,求圆的直径和半径。
典型例题 一个圆的周长是15.7 dm,它的直径和半径分别是多少分米?
思路分析 由公式C=πd和C=2πr可以分别推出d=C÷π和r=C÷π÷2,根据公式可以直接求出圆的直径和半径,也可以设圆的直径是x dm,根据公式列方程解答。
正确解答
方法一 直径:15.7÷3.14=5(dm)
半径:15.7÷3.14÷2=2.5(dm)
方法二
解:设它的直径是x dm。
3.14x=15.7
x=5
半径:5÷2=2.5(dm)
答:它的直径是5 dm,半径是2.5 dm。
知识巧记
圆的周长要想算,直径和π是关键;
两量相乘求结果,单位名称无需变。
备易错易混
误区一 判断:大圆的圆周率大,小圆的圆周率小。(√)
错解分析 此题错在没有理解圆周率的意义,圆周率是一个固定的数,不因圆的大小而改变。
错解改正 ×
温馨提示
圆周率是任意一个圆的周长与它的直径的比值,这个比值是一个固定的数。
误区二 判断:因为一个圆的周长总是它的直径的3倍多一些,所以π=3.14。(√)
错解分析 圆周率π是一个无限不循环小数,π=3.1415926535……在实际应用中常常取近似值,即π≈3.14。
错解改正 ×
温馨提示
圆周率π是一个无限不循环小数,3.14是它的近似值。
备综合能力
综合运用 运用圆周长的知识解决组合图形的周长问题
典型例题 如图,已知AB=120 m,BC=60 m,从点A到点C有①和②两条不同的路线,请你判断哪条路线比较近。
思路分析 要判断哪条路线比较近,就要把以AC为直径的圆的周长的一半与以AB和BC为直径的两个圆的周长的一半的和进行比较。
正确解答
路线①的长度: 3.14×(120+60)÷2
=3.14×180÷2
=282.6(m)
路线②的长度:
3.14×120÷2+3.14×60÷2
=188.4+94.2
=282.6(m)
282.6=282.6,两条路线一样近。
方法总结 由几个圆的一半组成的图形,如图一和图二所示,大圆的直径与几个小圆的直径和相等,大圆的周长的一半与几个小圆的周长的一半的和相等。
图一 图二
方法运用 运用转化法解决求捆扎物体的周长问题
典型例题 直径均为1 dm的4根管子被一根金属带紧紧地捆在一起,
如右图。求金属带的长度。(接头处忽略不计。)
思路分析 金属带的长度可以分成两部分,一部分是4条直径之和,另一部分是4个圆的周长之和,而4个圆的周长之和正好等于一个圆的周长。如图所示:
金属带的长度=4条直
径之和+4个圆的周
长之和
得出:金属带的长度等于一个圆的周长加上4条直径之和。
正确解答 3.14×1+1×4=7.14(dm)
答:金属带的长度是7.14 dm。
方法提示 解决此题的关键是运用转化法将求金属带的长度转化成求规则图形的周长。
备教学资源
祖冲之与圆周率
祖冲之是我国南北朝时期的人,今河北省涞水县人。他从小就阅读了许多科学、数学方面的书籍,他勤奋好学,刻苦实践,终于成为我国古代杰出的数学家、科学家。
祖冲之在数学上的杰出成就是关于圆周率的计算。秦汉以前,人们以“径一周三”作为圆周率,这就是“古率”。后来人们发现古率误差太大,圆周率应是“径一而周三有余”,不过究竟余多少,意见不一。祖冲之在前人成就的基础上,经过刻苦钻研,反复演算,求出π在3.1415926与3.1415927之间,并得出了π分数形式的近似值,取六位小数约是3.141593,它是分子、分母在1000以内最接近π的分数。祖冲之究竟用什么方法得出这一结果,现在无从考查。若设想他按刘徽的“割圆术”方法去求的话,就要计算到圆内接一万六千三百八十四边形,这需要花费多少时间和付出多大的劳动啊!由此可见他在数学上的顽强毅力和聪明才智是令人钦佩的。为了纪念祖冲之的杰出贡献,有些外国数学家建议把π=3.1415926……叫做“祖率”。
备教材内容
1.本课时学习的是教材62~64页的内容及相关习题。
2.教材首先从实际情境入手,通过让学生思考情境图中的问题引出圆的周长的概念。接着引导学生用不同的方法测量,自主发现圆的周长和直径的比值是一个固定值,从而引出圆周率的概念,并总结出圆的周长计算公式。例1是一个与圆的周长计算有关的实际问题,通过学生经常看到或使用的自行车引出问题,能让学生体会到数学知识的广泛应用。
3.这部分内容是在学生学习了周长的一般概念以及长方形、正方形的周长计算公式,并初步认识了圆的基础上进行教学的。它是学生初步研究曲线图形的开始,也是后面学习圆的面积以及圆柱、圆锥等知识的基础,是小学几何知识中的一项重要内容。
备教法学法
学生已经掌握长方形、正方形的周长计算公式,教师在此基础上先引导学生通过摸一摸、动手操作、猜想验证等活动,使学生经历整个探究知识的过程。再通过对圆周率的探究,培养学生主动探究的精神,提高动手操作能力和逻辑思维能力。最后引导学生推导圆的周长计算公式,提高学生的比较、分析能力,体会转化思想。
教学目标
1.理解圆周长的概念及圆周率的意义,掌握圆周长的计算公式。
2.经历操作、猜想、探究的学习活动,体会“化曲为直”的转化思想,积累数学活动经验。
3.了解数学文化,提高学习兴趣。
教学重难点
教学重点:
理解圆周率的意义,掌握圆周长的计算公式。
教学难点:
理解圆周率的意义。
备已学知识
1.周长:封闭图形一周的长度。
2.长方形(正方形)的周长:围成长方形(正方形)的四条边的长度和。
3.长方形的周长计算公式:C=(a+b)×2。
4.正方形的周长计算公式:C=4a。
备知识讲解
知识点一 圆的周长的意义及测量方法
问题导入 圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。(教材62页)
过程讲解
1.理解圆的周长的意义
2.圆的周长的测量方法
(1)滚动法。
①测量方法和过程:以直径为1.9 cm的圆为例,如下图:
[思想方法提示:将一个未曾学过的曲线图形的周长转化为可以直接测量的线段的长度,体现了转化思想。]
②测量结果:直径为1.9 cm的圆的周长大约是6 cm。
(2)绕绳法。
①测量方法和过程:以直径为1.9 cm的圆为例,如下图:
②测量结果:直径为1.9 cm的圆的周长大约是6 cm。
[方法提示:把一根没有弹性的绳子上的一点对准圆上的标记点A,并将绳子绕圆一周回到标记点A(A′)处,然后拉直绳子,测量出点A和点A′之间的长度,就是这个圆的周长。]
(3)直接测量法。
可以用卷尺或皮尺直接绕圆形物体一周进行测量。
小结:虽然以上方法都可以测量出圆的周长,但是这些方法都有一定的局限性,测得的数据都有一定的误差,因此需要探究一种常规的方法来求圆的周长。
归纳总结
1.围成圆的曲线的长是圆的周长。
2.测量圆的周长的方法不唯一,如滚动法、绕绳法、直接测量法等。
知识点二 圆周率的意义和圆的周长计算公式
问题导入 让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中,看看有什么发现。(教材63页)
物品名称 周长 直径 的比值 (保留两位小数)
过程讲解
1.选择物品,测量数据并完成表格
任意选择4个不同的圆形物品,分别测量出它们的直径和周长,并计算出周长和直径的比值,完成表格。(以编者测量的数据为例。)
物品名称 周长 直径 的比值 (保留两位小数)
圆形学具 6 cm 1.9 cm 3.16
圆形纸片 31.5 cm 10 cm 3.15
圆形瓶盖 10 cm 3.2 cm 3.13
圆形碗的碗口 34.5 cm 11 cm 3.14
2.观察并对比数据,找出规律
直径:11 cm>10 cm>3.2 cm>1.9 cm
周长:34.5 cm>31.5 cm>10 cm>6 cm
规律:圆的周长与它的直径有关,直径越长,周长越长。
3.观察表格中圆的周长和直径的比值,发现圆的周长与直径的关系
圆的周长和直径的比值:3.16、3.15、3.13、3.14。
发现:一个圆的周长总是它的直径的3倍多一些。
4.理解圆周率的意义
教育视点 我国数学家祖冲之是世界上第一个把圆周率的值精确到7位小数的人。
因为测量时存在一定的误差,所以这几个圆形物品的周长和直径的比值不相等。实际上这个比值是一个固定的数,我们把它叫做圆周率 。
圆周率是任意一个圆的周长与它的直径的比值,这个比值是一个固定的数,用字母π(pài)表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
[德育建议:引导学生经历动手操作、自主探究圆周率的过程,理解圆周率的意义,培养严谨认真的思维习惯。同时通过了解中国伟大的数学家祖冲之在圆周率方面的巨大贡献,感受古代人民非凡的智慧,激发学生的爱国情感。]
5.根据圆的周长与直径的关系推导圆的周长计算公式
(1)=圆周率 圆的周长=直径×圆周率
(2)
圆的周长=半径×2×圆周率
归纳总结
1.
π=3.1415926535……
2.圆的周长=直径×圆周率或圆的周长=半径×2×圆周率。如果用C表示圆的周长,用r表示圆的半径,用d表示圆的直径,那么圆的周长计算公式是C=πd或C=2πr。
拓展提高
1.圆的周长与它的半径、直径的关系:(1)圆的半径或直径扩大到原来的几倍,它的周长也扩大到原来的几倍。(2)圆的半径或直径缩小到原来的几分之一,它的周长也缩小到原来的几分之一。
2.半圆的周长和圆的周长的一半。
知识点三 圆的周长计算公式的应用
应用一 已知圆的半径,求圆的周长。
典型例题 一辆自行车轮子的半径大约是33 cm。这辆自行车轮子转1圈,大约可以走多远?(结果保留整米数。)小明家离学校1 km,骑车从家到学校,轮子大约转了多少圈?(教材64页例1)
思路分析 求这辆自行车轮子转1圈,大约可以走多远,就是求这辆自行车轮子的周长。自行车轮子是圆形的,已知它的半径,可以直接应用公式C=2πr求出它的周长。
因为小明家离学校1 km,所以求小明骑车从家到学校,轮子大约转了多少圈,就是求1 km里面大约有多少个自行车轮子的周长,即用1 km除以自行车轮子的周长。
正确解答
2×3.14×33=207.24(cm)≈2(m) 1 km=1000 m 1000÷2=500(圈)
答:这辆自行车轮子转1圈,大约可以走2 m。骑车从家到学校,轮子大约转了500圈。
应用二 已知圆的直径,求圆的周长。
典型例题 一个圆形花坛的直径是20 m,它的周长是多少米?
思路分析 已知圆形花坛的直径,可以直接应用公式C=πd求出它的周长。
正确解答 3.14×20=62.8(m)
答:它的周长是62.8 m。
应用三 已知圆的周长,求圆的直径和半径。
典型例题 一个圆的周长是15.7 dm,它的直径和半径分别是多少分米?
思路分析 由公式C=πd和C=2πr可以分别推出d=C÷π和r=C÷π÷2,根据公式可以直接求出圆的直径和半径,也可以设圆的直径是x dm,根据公式列方程解答。
正确解答
方法一 直径:15.7÷3.14=5(dm)
半径:15.7÷3.14÷2=2.5(dm)
方法二
解:设它的直径是x dm。
3.14x=15.7
x=5
半径:5÷2=2.5(dm)
答:它的直径是5 dm,半径是2.5 dm。
知识巧记
圆的周长要想算,直径和π是关键;
两量相乘求结果,单位名称无需变。
备易错易混
误区一 判断:大圆的圆周率大,小圆的圆周率小。(√)
错解分析 此题错在没有理解圆周率的意义,圆周率是一个固定的数,不因圆的大小而改变。
错解改正 ×
温馨提示
圆周率是任意一个圆的周长与它的直径的比值,这个比值是一个固定的数。
误区二 判断:因为一个圆的周长总是它的直径的3倍多一些,所以π=3.14。(√)
错解分析 圆周率π是一个无限不循环小数,π=3.1415926535……在实际应用中常常取近似值,即π≈3.14。
错解改正 ×
温馨提示
圆周率π是一个无限不循环小数,3.14是它的近似值。
备综合能力
综合运用 运用圆周长的知识解决组合图形的周长问题
典型例题 如图,已知AB=120 m,BC=60 m,从点A到点C有①和②两条不同的路线,请你判断哪条路线比较近。
思路分析 要判断哪条路线比较近,就要把以AC为直径的圆的周长的一半与以AB和BC为直径的两个圆的周长的一半的和进行比较。
正确解答
路线①的长度: 3.14×(120+60)÷2
=3.14×180÷2
=282.6(m)
路线②的长度:
3.14×120÷2+3.14×60÷2
=188.4+94.2
=282.6(m)
282.6=282.6,两条路线一样近。
方法总结 由几个圆的一半组成的图形,如图一和图二所示,大圆的直径与几个小圆的直径和相等,大圆的周长的一半与几个小圆的周长的一半的和相等。
图一 图二
方法运用 运用转化法解决求捆扎物体的周长问题
典型例题 直径均为1 dm的4根管子被一根金属带紧紧地捆在一起,
如右图。求金属带的长度。(接头处忽略不计。)
思路分析 金属带的长度可以分成两部分,一部分是4条直径之和,另一部分是4个圆的周长之和,而4个圆的周长之和正好等于一个圆的周长。如图所示:
金属带的长度=4条直
径之和+4个圆的周
长之和
得出:金属带的长度等于一个圆的周长加上4条直径之和。
正确解答 3.14×1+1×4=7.14(dm)
答:金属带的长度是7.14 dm。
方法提示 解决此题的关键是运用转化法将求金属带的长度转化成求规则图形的周长。
备教学资源
祖冲之与圆周率
祖冲之是我国南北朝时期的人,今河北省涞水县人。他从小就阅读了许多科学、数学方面的书籍,他勤奋好学,刻苦实践,终于成为我国古代杰出的数学家、科学家。
祖冲之在数学上的杰出成就是关于圆周率的计算。秦汉以前,人们以“径一周三”作为圆周率,这就是“古率”。后来人们发现古率误差太大,圆周率应是“径一而周三有余”,不过究竟余多少,意见不一。祖冲之在前人成就的基础上,经过刻苦钻研,反复演算,求出π在3.1415926与3.1415927之间,并得出了π分数形式的近似值,取六位小数约是3.141593,它是分子、分母在1000以内最接近π的分数。祖冲之究竟用什么方法得出这一结果,现在无从考查。若设想他按刘徽的“割圆术”方法去求的话,就要计算到圆内接一万六千三百八十四边形,这需要花费多少时间和付出多大的劳动啊!由此可见他在数学上的顽强毅力和聪明才智是令人钦佩的。为了纪念祖冲之的杰出贡献,有些外国数学家建议把π=3.1415926……叫做“祖率”。
