5.1《圆的认识》(教案)-六年级上册数学人教版
文档属性
| 名称 | 5.1《圆的认识》(教案)-六年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 13:32:44 | ||
图片预览




文档简介
《圆的认识》教学设计
备教材内容
1.本课时学习的是教材57~59页的内容及相关习题。
2.本课时教学圆的认识。教材首先通过观察自然界及建筑中的图形引出圆,为探究圆的特征做好准备。然后引导学生进行探究活动,在探究活动中认识圆心、半径和直径,并了解它们之间的关系,掌握圆的特征,明确圆心和半径的作用,掌握画圆的方法。最后安排了一个实践活动:根据圆的对称性,利用圆规和直尺绘制图案。
3.本课时是深入学习曲线图形的开始,也是学习圆的周长和面积的基础。
备教法学法
学生已经掌握了长方形、正方形、平行四边形、三角形等一些平面图形的相关知识,教师教学时可以在此基础上先认识曲线图形——圆。再引导学生动手操作,掌握画圆的方法。通过小组合作学习、动手操作、主动探究等活动,培养学生的创新意识。明确用符号表示圆心、半径和直径。提高学生的作图能力及抽象概括能力。
教学目标
1.使学生学会用圆规画圆,认识圆的各部分名称,理解并掌握圆的特征。
2.经历画圆的过程,提高学生动手操作、观察比较、推理和概括能力,发展空间观念。
3.感受数学与生活的紧密联系,用圆的相关知识解释生活中的一些现象;感受古代数学的博
大精深,激发学生对数学的学习兴趣。
教学重难点
教学重点:
理解圆的本质特征“一中同长”。
教学难点:
探索圆的本质特征。
备已学知识
1.长方形:对边平行且相等;四个角都是直角。
2.正方形:对边平行且四条边都相等;四个角都是直角。
3.平行四边形:对边平行且相等;对角相等。
4.三角形:两边之和大于第三边;三个内角的和是180°。
备知识讲解
知识点一 圆的认识和画圆的方法
问题导入 生活中,圆形的物体随处可见。你能说说自己见过的圆吗?你能想办法在纸上画一个圆吗?(教材57页)
过程讲解
1.初步感知圆
观察下面的图片,从奇妙的自然界到文明的人类社会,从精巧的手工艺品到气势宏伟的各种建筑……到处都可以看到大大小小的圆。
2.探究画圆的方法
(1)借助实物画圆。
(2)系线画圆。
[操作指导:用图钉、细线和笔画圆时,图钉要固定好,细线不能有弹性且要拉直。]
(3)用圆规画圆。
①认识圆规。
如下图所示:
[画法提示:用圆规画圆的注意事项:(1)带有针尖的脚不能移动;(2)两脚之间的距离不能改变。]
②画法展示。
[方法提示:对比三种画圆的方法,用圆规画圆的方法最实用。]
由画圆过程发现,圆是由曲线围成的封闭图形,无顶点。
归纳总结
1.一条线段绕着它固定的一端在平面上旋转一周,它的另一端就会画出一条封闭的曲线,这条封闭的曲线就是圆。
2.用圆规画圆的方法:
定好两脚之间的距离。把带有针尖的脚固定在一点上。把装有铅笔的脚旋转一周,就画出了一个圆。
知识点二 圆的各部分名称
问题导入 观察右图,了解圆的各部分名称。(教材58页)
过程讲解
1.认识圆心
(1)圆心的意义:如图,用圆规画圆时,针尖所在的点叫做圆心。
圆心一般用字母O表示,如右图。
(2)圆心的作用:圆心决定圆的位置。
重点提示 用圆规画圆时,圆规两脚之间的距离就是所画圆的半径。
2.认识半径
(1)半径的意义:连接圆心和圆上任意一点的线段叫做半径。
半径一般用字母r表示,如上图。
(2)半径的作用:半径决定圆的大小。半径越长,圆越大;半径越短,圆越小。
(3)判断半径的方法:半径是一条线段,它的一端在圆心,另一端在圆上。
3.认识直径
(1)直径的意义:通过圆心并且两端都在圆上的线段叫做直径。
直径一般用字母d表示,如右图。
(2)判断直径的方法:①是一条通过圆心的线段;②线段的两端都在圆上;③是圆中最长的线段。
归纳总结
圆的各部分名称:
拓展提高
1.圆的数学定义:圆是到定点的距离等于定长的所有点的集合。定点指的是圆心,定长指的是半径的长度。
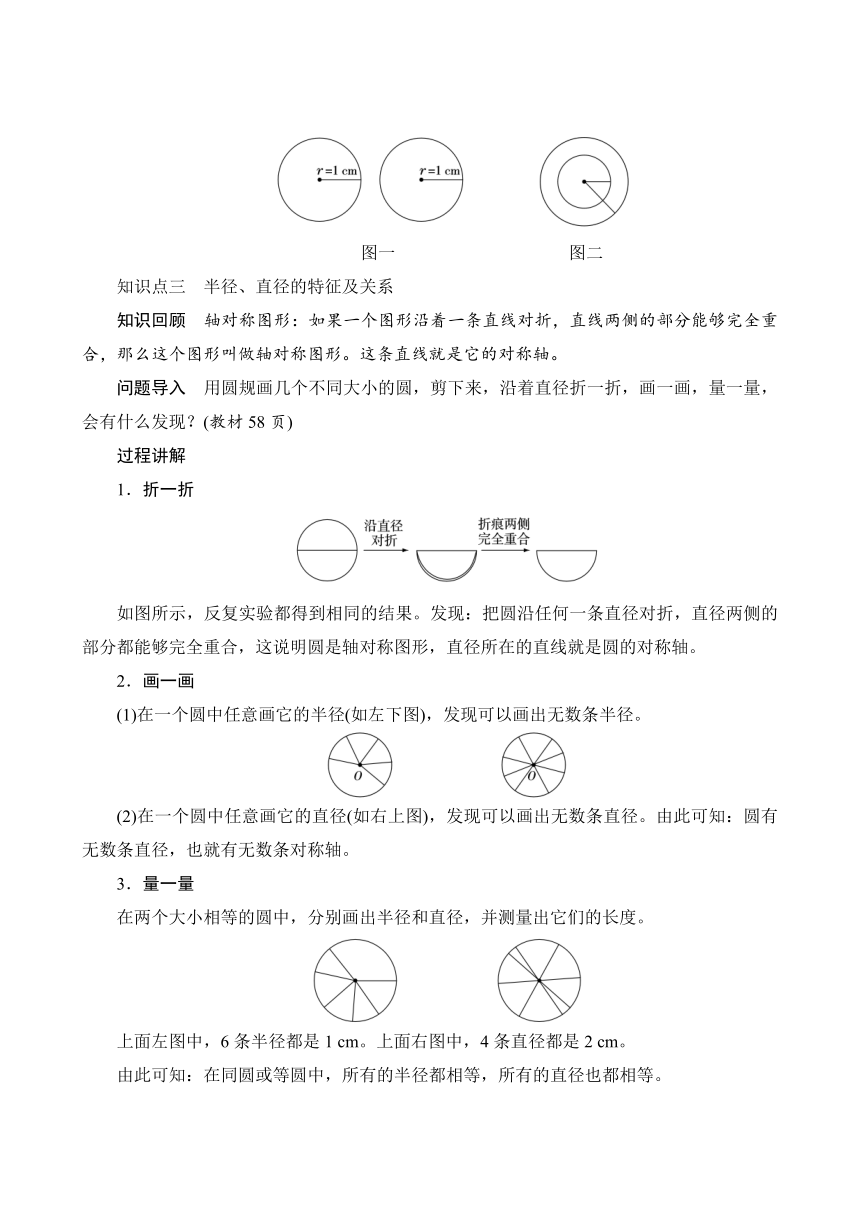
2.等圆:半径相等的圆叫做等圆。等圆经过平移可以完全重合。如图一。
3.同心圆:圆心重合、半径不相等的圆叫做同心圆。如图二。
图一 图二
知识点三 半径、直径的特征及关系
知识回顾 轴对称图形:如果一个图形沿着一条直线对折,直线两侧的部分能够完全重合,那么这个图形叫做轴对称图形。这条直线就是它的对称轴。
问题导入 用圆规画几个不同大小的圆,剪下来,沿着直径折一折,画一画,量一量,会有什么发现?(教材58页)
过程讲解
1.折一折
如图所示,反复实验都得到相同的结果。发现:把圆沿任何一条直径对折,直径两侧的部分都能够完全重合,这说明圆是轴对称图形,直径所在的直线就是圆的对称轴。
2.画一画
(1)在一个圆中任意画它的半径(如左下图),发现可以画出无数条半径。
(2)在一个圆中任意画它的直径(如右上图),发现可以画出无数条直径。由此可知:圆有无数条直径,也就有无数条对称轴。
3.量一量
在两个大小相等的圆中,分别画出半径和直径,并测量出它们的长度。
上面左图中,6条半径都是1 cm。上面右图中,4条直径都是2 cm。
由此可知:在同圆或等圆中,所有的半径都相等,所有的直径也都相等。
4.算一算
上面的两个圆是等圆,且这两个圆的半径都是1 cm,直径都是2 cm。
(1)算一算半径是直径的几分之几,直径是半径的几倍。
灵活应用 在同圆或等圆中,已知直径求半径,用直径除以2;已知半径求直径,用半径乘2。
1÷2= 2÷1=2
(2)明确半径和直径的关系:在同圆或等圆中,半径的长度是直径的,直径的长度是半径的2倍。
归纳总结
1.圆是轴对称图形,直径所在的直线是圆的对称轴,圆有无数条对称轴。
2.在同圆或等圆中,所有的半径都相等,所有的直径也都相等。
3.在同圆或等圆中:r=或d=2r。
拓展提高
1.在同圆或等圆中,半径扩大到原来的几倍,直径也扩大到原来的几倍;半径缩小到原来的几分之一,直径也缩小到原来的几分之一。
2.可以用对折法找到前面用茶杯盖画出的圆的圆心,即将圆剪下来,沿不同的方向对折两次,折痕的交点就是圆心。如下图所示:
知识巧记
圆的认识并不难,心径特征要记全;
圆心一点定位置,大小两径说了算;
圆规画圆很简单,半径就在两脚间;
圆心定位靠针尖,笔尖一转就画完。
知识点四 用圆规和直尺绘制与圆有关的图案
问题(1)导入 用圆可以设计许多漂亮的图案。你能用圆规和直尺一步一步画出下面的图案吗?(教材59页)
过程讲解
1.观图,找出图案的特点
此图案是由1个大圆和4个相等的小半圆组合而成的,图案中的白色部分是4个小半圆的重叠部分。
2.画图步骤及方法
问题(2)导入 请你试着用圆规和直尺画一画下面的图形。(教材59页)
图一 图二
过程讲解
1.画图一
(1)观图,找出图案的特点。
(2)画图步骤及方法。
重点提示 绘图的关键是要确定某个圆或半圆的圆心和半径(或直径),因为圆心和半径(或直径)分别决定圆的位置和大小。
2.画图二
(1)观图,找出图案的特点。
(2)画图步骤及方法。
[德育建议:引导学生动手操作,借助圆规和直尺,根据圆的特征设计图案,进一步理解圆的特征,感受图形之美,学会欣赏美、创造美。]
归纳总结
用圆规和直尺绘制图案的步骤及方法:(1)观察图案的特点;(2)用圆规和直尺一步一步地画图;(3)根据已知图案去掉多余的线条并涂上相应的颜色。
备易错易混
误区一 判断。
(1)圆的半径和直径分别相等。(√)
(2)通过圆心并且两端都在圆上的直线叫做直径。(√)
错解分析 (1)题错在没有考虑半径和直径分别相等的前提条件是在同圆或等圆中。(2)题错在没有理解直径的意义,直径是线段而不是直线。
错解改正 (1)× (2)×
温馨提示
1.在同圆或等圆中,所有的半径都相等,所有的直径也都相等。2.半径和直径都是线段而不是直线。
误区二 判断:在同一个圆中,每条直径都能分成两条半径,所以两条半径一定能组成一条直径。(√)
错解分析 此题错在对半径和直径的意义理解不清。因为在同一个圆中d=2r,所以两条半径的长度和与一条直径的长度相等,但当两条半径不在同一条直线上时,它们就不能组成一条直径。
错解改正 ×
温馨提示
在同一个圆中,一条直径的长度等于两条半径的长度和,但只有在同一条直线上的两条半径才能组成一条直径。
误区三 判断:在同一平面内的任意两个圆都关于一条直线成轴对称。(√)
错解分析 在同一平面内的两个圆关于一条直线成轴对称,这两个圆的半径或直径一定相等。因为在同一平面内的任意两个圆的半径或直径并不一定相等,所以在同一平面内的任意两个圆不一定关于一条直线成轴对称。
错解改正 ×
温馨提示
在同一平面内,关于一条直线成轴对称的两个图形的形状、大小一定完全相同。
备综合能力
思维开放 根据圆的特征解决找圆的直径的问题
典型例题 有一张圆形铁片,没有标明圆心,你能找出它的直径吗?
思路分析 圆形铁片无法对折,不能用对折法找出直径。在没有标明圆心的情况下,可以根据圆的特征找出直径,直径是圆中最长的线段;也可以紧贴圆形铁片边缘在圆形铁片外画一个正方形,根据圆的直径的长度等于这个正方形的边长找出直径。方法不唯一。
正确解答 方法不唯一,仅举四种方法。
方法一 把直尺的0刻度固定在圆形铁片边缘的任意一点上,移动直尺的另一端,量出的最长线段,就是圆形铁片的直径,如图一,图中线段AD最长,线段AD就是这张圆形铁片的直径。
图一 图二
方法二 紧贴圆形铁片边缘在圆形铁片外画一个正方形,正方形和圆形铁片的交点分别是点A、B、C、D,连接AC、BD。线段AC、BD都是这张圆形铁片的直径,如图二。
图三 图四
方法三 把圆形铁片放在平面上,先紧贴圆形铁片边缘上一点画一条直线AB,然后在圆形铁片的另一侧边缘上画直线AB的平行线CD,直线AB、CD与圆形铁片的交点分别是点E、F,连接EF,线段EF就是这张圆形铁片的直径,如图三。
方法四 在圆形铁片上任意画一条线段CD,使线段CD的两端都在圆形铁片的边缘上,然后过线段CD的中点画它的垂线,这条垂线与圆形铁片相交于A、B两点,线段AB就是这张圆形铁片的直径,如图四。
方法总结 确定一个圆形物体的直径或半径的方法较多,要根据实际情况选择合适的方法,可以折叠的用对折法较简单,不可以折叠的用方法四更容易操作。
综合运用 运用圆和三角形的知识解决实际问题
典型例题 右面是由三个等圆组成的平面图形。依次连接O1、O2和O3
三个圆心围成一个三角形,这个三角形的三个内角各是多少度?
思路分析
正确解答 这个三角形的三个内角都是60°。
方法总结 解决此题的关键是明确在等圆中,所有的半径(或直径)都相等。
思维开放 运用轴对称图形的特征解决实际问题
典型例题 在方格纸上画圆,使点A和点B都在圆上,可以画出多少个这样的圆?这些圆的圆心所在的纵向直线与线段AB有什么关系?
思路分析 在点A和点B中间的竖线l上(如图)任取一点O,以OA(或OB)为半径画圆,这样的圆能画出无数个。观察发现,这些圆的圆心所在的直线l垂直于线段AB,且平分线段AB。
正确解答 可以画出无数个这样的圆,这些圆的圆心所在的纵向直线垂直于线段AB,且平分线段AB。
方法总结 平分且垂直于线段的直线上的任意一点到线段两端的距离都相等。
方法运用 运用观察法解决实际问题
典型例题 在方格纸上画出下面轴对称图形的另一半。
思路分析 画轴对称图形的另一半,关键在于确定已知图形的关键点或关键线段,并根据轴对称图形的特征找到对应点或对应线段。圆是曲线图形,它的关键点就是圆心,关键线段就是半径或直径。
以画圆O1关于对称轴的轴对称图形为例。
找圆心O1的对应点:圆心O1距对称轴2个小格,在对称轴另一侧的同一条直线上,距对称轴2个小格处确定点O1′,点O1′即为圆心O1的对应点,如下图。
确定圆O1′的半径:圆O1的半径是1个小格的长度,所以圆O1′的半径也是1个小格的长度。
画圆O1′:以点O1′为圆心,以1个小格的长度为半径画圆,即为圆O1关于对称轴的轴对称图形,如下图。
用这种方法可以在方格纸上画出轴对称图形的另一半。
正确解答
方法总结 画有关圆的轴对称图形的另一半时,一般圆心是关键点,半径或直径是关键线段。
备教学资源
我国古代著作中的“圆”
早在两千多年前,我国古代就有了关于圆的精确记载。墨子在他的著作中这样描述:圆,一中同长也。所谓“一中”,就是指一个圆心。“同长”指半径一样长,直径也一样长。
《周髀算经》中有这样的记载:圆出于方,方出于矩。所谓“圆出于方”,就是说最初的圆并不是用现在的圆规画出来的,而是由正方形不断切割而来的。
备教材内容
1.本课时学习的是教材57~59页的内容及相关习题。
2.本课时教学圆的认识。教材首先通过观察自然界及建筑中的图形引出圆,为探究圆的特征做好准备。然后引导学生进行探究活动,在探究活动中认识圆心、半径和直径,并了解它们之间的关系,掌握圆的特征,明确圆心和半径的作用,掌握画圆的方法。最后安排了一个实践活动:根据圆的对称性,利用圆规和直尺绘制图案。
3.本课时是深入学习曲线图形的开始,也是学习圆的周长和面积的基础。
备教法学法
学生已经掌握了长方形、正方形、平行四边形、三角形等一些平面图形的相关知识,教师教学时可以在此基础上先认识曲线图形——圆。再引导学生动手操作,掌握画圆的方法。通过小组合作学习、动手操作、主动探究等活动,培养学生的创新意识。明确用符号表示圆心、半径和直径。提高学生的作图能力及抽象概括能力。
教学目标
1.使学生学会用圆规画圆,认识圆的各部分名称,理解并掌握圆的特征。
2.经历画圆的过程,提高学生动手操作、观察比较、推理和概括能力,发展空间观念。
3.感受数学与生活的紧密联系,用圆的相关知识解释生活中的一些现象;感受古代数学的博
大精深,激发学生对数学的学习兴趣。
教学重难点
教学重点:
理解圆的本质特征“一中同长”。
教学难点:
探索圆的本质特征。
备已学知识
1.长方形:对边平行且相等;四个角都是直角。
2.正方形:对边平行且四条边都相等;四个角都是直角。
3.平行四边形:对边平行且相等;对角相等。
4.三角形:两边之和大于第三边;三个内角的和是180°。
备知识讲解
知识点一 圆的认识和画圆的方法
问题导入 生活中,圆形的物体随处可见。你能说说自己见过的圆吗?你能想办法在纸上画一个圆吗?(教材57页)
过程讲解
1.初步感知圆
观察下面的图片,从奇妙的自然界到文明的人类社会,从精巧的手工艺品到气势宏伟的各种建筑……到处都可以看到大大小小的圆。
2.探究画圆的方法
(1)借助实物画圆。
(2)系线画圆。
[操作指导:用图钉、细线和笔画圆时,图钉要固定好,细线不能有弹性且要拉直。]
(3)用圆规画圆。
①认识圆规。
如下图所示:
[画法提示:用圆规画圆的注意事项:(1)带有针尖的脚不能移动;(2)两脚之间的距离不能改变。]
②画法展示。
[方法提示:对比三种画圆的方法,用圆规画圆的方法最实用。]
由画圆过程发现,圆是由曲线围成的封闭图形,无顶点。
归纳总结
1.一条线段绕着它固定的一端在平面上旋转一周,它的另一端就会画出一条封闭的曲线,这条封闭的曲线就是圆。
2.用圆规画圆的方法:
定好两脚之间的距离。把带有针尖的脚固定在一点上。把装有铅笔的脚旋转一周,就画出了一个圆。
知识点二 圆的各部分名称
问题导入 观察右图,了解圆的各部分名称。(教材58页)
过程讲解
1.认识圆心
(1)圆心的意义:如图,用圆规画圆时,针尖所在的点叫做圆心。
圆心一般用字母O表示,如右图。
(2)圆心的作用:圆心决定圆的位置。
重点提示 用圆规画圆时,圆规两脚之间的距离就是所画圆的半径。
2.认识半径
(1)半径的意义:连接圆心和圆上任意一点的线段叫做半径。
半径一般用字母r表示,如上图。
(2)半径的作用:半径决定圆的大小。半径越长,圆越大;半径越短,圆越小。
(3)判断半径的方法:半径是一条线段,它的一端在圆心,另一端在圆上。
3.认识直径
(1)直径的意义:通过圆心并且两端都在圆上的线段叫做直径。
直径一般用字母d表示,如右图。
(2)判断直径的方法:①是一条通过圆心的线段;②线段的两端都在圆上;③是圆中最长的线段。
归纳总结
圆的各部分名称:
拓展提高
1.圆的数学定义:圆是到定点的距离等于定长的所有点的集合。定点指的是圆心,定长指的是半径的长度。
2.等圆:半径相等的圆叫做等圆。等圆经过平移可以完全重合。如图一。
3.同心圆:圆心重合、半径不相等的圆叫做同心圆。如图二。
图一 图二
知识点三 半径、直径的特征及关系
知识回顾 轴对称图形:如果一个图形沿着一条直线对折,直线两侧的部分能够完全重合,那么这个图形叫做轴对称图形。这条直线就是它的对称轴。
问题导入 用圆规画几个不同大小的圆,剪下来,沿着直径折一折,画一画,量一量,会有什么发现?(教材58页)
过程讲解
1.折一折
如图所示,反复实验都得到相同的结果。发现:把圆沿任何一条直径对折,直径两侧的部分都能够完全重合,这说明圆是轴对称图形,直径所在的直线就是圆的对称轴。
2.画一画
(1)在一个圆中任意画它的半径(如左下图),发现可以画出无数条半径。
(2)在一个圆中任意画它的直径(如右上图),发现可以画出无数条直径。由此可知:圆有无数条直径,也就有无数条对称轴。
3.量一量
在两个大小相等的圆中,分别画出半径和直径,并测量出它们的长度。
上面左图中,6条半径都是1 cm。上面右图中,4条直径都是2 cm。
由此可知:在同圆或等圆中,所有的半径都相等,所有的直径也都相等。
4.算一算
上面的两个圆是等圆,且这两个圆的半径都是1 cm,直径都是2 cm。
(1)算一算半径是直径的几分之几,直径是半径的几倍。
灵活应用 在同圆或等圆中,已知直径求半径,用直径除以2;已知半径求直径,用半径乘2。
1÷2= 2÷1=2
(2)明确半径和直径的关系:在同圆或等圆中,半径的长度是直径的,直径的长度是半径的2倍。
归纳总结
1.圆是轴对称图形,直径所在的直线是圆的对称轴,圆有无数条对称轴。
2.在同圆或等圆中,所有的半径都相等,所有的直径也都相等。
3.在同圆或等圆中:r=或d=2r。
拓展提高
1.在同圆或等圆中,半径扩大到原来的几倍,直径也扩大到原来的几倍;半径缩小到原来的几分之一,直径也缩小到原来的几分之一。
2.可以用对折法找到前面用茶杯盖画出的圆的圆心,即将圆剪下来,沿不同的方向对折两次,折痕的交点就是圆心。如下图所示:
知识巧记
圆的认识并不难,心径特征要记全;
圆心一点定位置,大小两径说了算;
圆规画圆很简单,半径就在两脚间;
圆心定位靠针尖,笔尖一转就画完。
知识点四 用圆规和直尺绘制与圆有关的图案
问题(1)导入 用圆可以设计许多漂亮的图案。你能用圆规和直尺一步一步画出下面的图案吗?(教材59页)
过程讲解
1.观图,找出图案的特点
此图案是由1个大圆和4个相等的小半圆组合而成的,图案中的白色部分是4个小半圆的重叠部分。
2.画图步骤及方法
问题(2)导入 请你试着用圆规和直尺画一画下面的图形。(教材59页)
图一 图二
过程讲解
1.画图一
(1)观图,找出图案的特点。
(2)画图步骤及方法。
重点提示 绘图的关键是要确定某个圆或半圆的圆心和半径(或直径),因为圆心和半径(或直径)分别决定圆的位置和大小。
2.画图二
(1)观图,找出图案的特点。
(2)画图步骤及方法。
[德育建议:引导学生动手操作,借助圆规和直尺,根据圆的特征设计图案,进一步理解圆的特征,感受图形之美,学会欣赏美、创造美。]
归纳总结
用圆规和直尺绘制图案的步骤及方法:(1)观察图案的特点;(2)用圆规和直尺一步一步地画图;(3)根据已知图案去掉多余的线条并涂上相应的颜色。
备易错易混
误区一 判断。
(1)圆的半径和直径分别相等。(√)
(2)通过圆心并且两端都在圆上的直线叫做直径。(√)
错解分析 (1)题错在没有考虑半径和直径分别相等的前提条件是在同圆或等圆中。(2)题错在没有理解直径的意义,直径是线段而不是直线。
错解改正 (1)× (2)×
温馨提示
1.在同圆或等圆中,所有的半径都相等,所有的直径也都相等。2.半径和直径都是线段而不是直线。
误区二 判断:在同一个圆中,每条直径都能分成两条半径,所以两条半径一定能组成一条直径。(√)
错解分析 此题错在对半径和直径的意义理解不清。因为在同一个圆中d=2r,所以两条半径的长度和与一条直径的长度相等,但当两条半径不在同一条直线上时,它们就不能组成一条直径。
错解改正 ×
温馨提示
在同一个圆中,一条直径的长度等于两条半径的长度和,但只有在同一条直线上的两条半径才能组成一条直径。
误区三 判断:在同一平面内的任意两个圆都关于一条直线成轴对称。(√)
错解分析 在同一平面内的两个圆关于一条直线成轴对称,这两个圆的半径或直径一定相等。因为在同一平面内的任意两个圆的半径或直径并不一定相等,所以在同一平面内的任意两个圆不一定关于一条直线成轴对称。
错解改正 ×
温馨提示
在同一平面内,关于一条直线成轴对称的两个图形的形状、大小一定完全相同。
备综合能力
思维开放 根据圆的特征解决找圆的直径的问题
典型例题 有一张圆形铁片,没有标明圆心,你能找出它的直径吗?
思路分析 圆形铁片无法对折,不能用对折法找出直径。在没有标明圆心的情况下,可以根据圆的特征找出直径,直径是圆中最长的线段;也可以紧贴圆形铁片边缘在圆形铁片外画一个正方形,根据圆的直径的长度等于这个正方形的边长找出直径。方法不唯一。
正确解答 方法不唯一,仅举四种方法。
方法一 把直尺的0刻度固定在圆形铁片边缘的任意一点上,移动直尺的另一端,量出的最长线段,就是圆形铁片的直径,如图一,图中线段AD最长,线段AD就是这张圆形铁片的直径。
图一 图二
方法二 紧贴圆形铁片边缘在圆形铁片外画一个正方形,正方形和圆形铁片的交点分别是点A、B、C、D,连接AC、BD。线段AC、BD都是这张圆形铁片的直径,如图二。
图三 图四
方法三 把圆形铁片放在平面上,先紧贴圆形铁片边缘上一点画一条直线AB,然后在圆形铁片的另一侧边缘上画直线AB的平行线CD,直线AB、CD与圆形铁片的交点分别是点E、F,连接EF,线段EF就是这张圆形铁片的直径,如图三。
方法四 在圆形铁片上任意画一条线段CD,使线段CD的两端都在圆形铁片的边缘上,然后过线段CD的中点画它的垂线,这条垂线与圆形铁片相交于A、B两点,线段AB就是这张圆形铁片的直径,如图四。
方法总结 确定一个圆形物体的直径或半径的方法较多,要根据实际情况选择合适的方法,可以折叠的用对折法较简单,不可以折叠的用方法四更容易操作。
综合运用 运用圆和三角形的知识解决实际问题
典型例题 右面是由三个等圆组成的平面图形。依次连接O1、O2和O3
三个圆心围成一个三角形,这个三角形的三个内角各是多少度?
思路分析
正确解答 这个三角形的三个内角都是60°。
方法总结 解决此题的关键是明确在等圆中,所有的半径(或直径)都相等。
思维开放 运用轴对称图形的特征解决实际问题
典型例题 在方格纸上画圆,使点A和点B都在圆上,可以画出多少个这样的圆?这些圆的圆心所在的纵向直线与线段AB有什么关系?
思路分析 在点A和点B中间的竖线l上(如图)任取一点O,以OA(或OB)为半径画圆,这样的圆能画出无数个。观察发现,这些圆的圆心所在的直线l垂直于线段AB,且平分线段AB。
正确解答 可以画出无数个这样的圆,这些圆的圆心所在的纵向直线垂直于线段AB,且平分线段AB。
方法总结 平分且垂直于线段的直线上的任意一点到线段两端的距离都相等。
方法运用 运用观察法解决实际问题
典型例题 在方格纸上画出下面轴对称图形的另一半。
思路分析 画轴对称图形的另一半,关键在于确定已知图形的关键点或关键线段,并根据轴对称图形的特征找到对应点或对应线段。圆是曲线图形,它的关键点就是圆心,关键线段就是半径或直径。
以画圆O1关于对称轴的轴对称图形为例。
找圆心O1的对应点:圆心O1距对称轴2个小格,在对称轴另一侧的同一条直线上,距对称轴2个小格处确定点O1′,点O1′即为圆心O1的对应点,如下图。
确定圆O1′的半径:圆O1的半径是1个小格的长度,所以圆O1′的半径也是1个小格的长度。
画圆O1′:以点O1′为圆心,以1个小格的长度为半径画圆,即为圆O1关于对称轴的轴对称图形,如下图。
用这种方法可以在方格纸上画出轴对称图形的另一半。
正确解答
方法总结 画有关圆的轴对称图形的另一半时,一般圆心是关键点,半径或直径是关键线段。
备教学资源
我国古代著作中的“圆”
早在两千多年前,我国古代就有了关于圆的精确记载。墨子在他的著作中这样描述:圆,一中同长也。所谓“一中”,就是指一个圆心。“同长”指半径一样长,直径也一样长。
《周髀算经》中有这样的记载:圆出于方,方出于矩。所谓“圆出于方”,就是说最初的圆并不是用现在的圆规画出来的,而是由正方形不断切割而来的。
