9.1 成比例线段课件
图片预览








文档简介
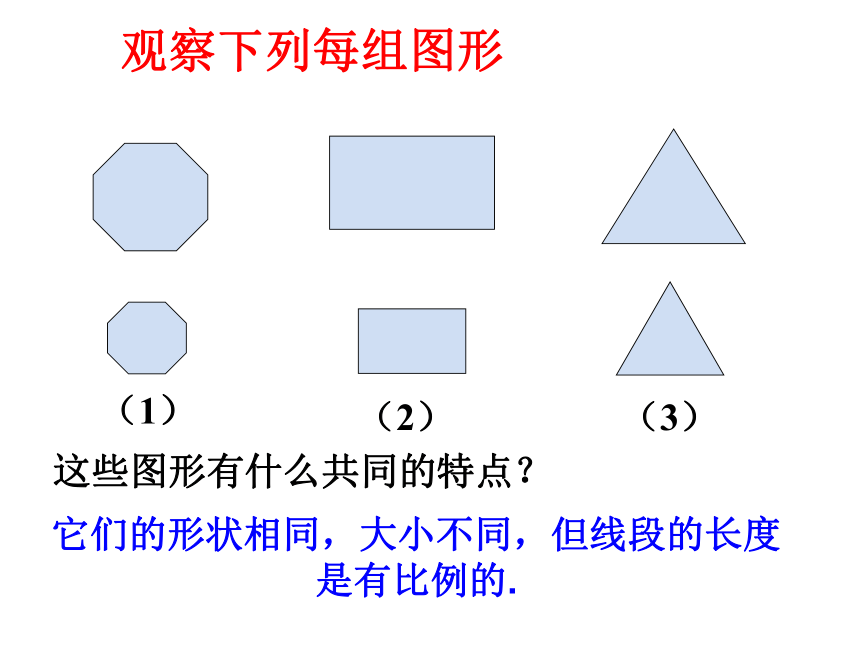
课件20张PPT。 线段的比(1)全等形指能够完全重合的两个图形,即它们的形状和大小完全相同.复习回顾问题:在现实生活中,同学们还见过哪些形状相同但大小不一定相等的图形? 议一议黄山松天坛非洲象观察下列每组图形(1)(2)(3)这些图形有什么共同的特点?它们的形状相同,大小不同,但线段的长度是有比例的.(1)如图,如果把大树和小颖的高分别看成图中的两条虚线段AB,CD,那么这两条线段的长度比是多少?(2)已知小颖的身高是1.6m,大树的实际高度是多少?CDAB答案:4.7:1答案:约为7.52m. 两条线段长度的比与所采用的长度单位有没有关系? 答:线段的长度比与采用的长度单位无关.但两条线段要采用同一个长度单位.如:上题中大树的高度和小颖的身高可以同时 用米(m)作单位,即:7.52m和1.6m;也可以同时用厘米(cm)作单位,即752cm和160cm.而它们的比值是一样的,
即7.52:1.6=752:160(1)两条线段的比:如果选用同一个长度单位,量得两
条线段AB,CD的长度分别是m,n,那么就说这两条线段的
比AB:CD=m:n,或写成 其中,线段AB,CD分别叫
做这个线段比的前项和后项.(2)引入比值k的表示方法:如果把 表示成比值k,
那么 ,或 AB=k·CD.注意:引入比值k的方法是解决比例问题的一种重要方法,以后经常会用到. 练习1:已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b.解:a :b = 320 :120 = 8 :3或: 练习2:在Rt△ABC中,∠C=90°, CD是AB边的中线,求CD :AB.解:CD:AB = 1 :2D课内练习 例1:在某市城区地图(比例尺是1:9000)上,新安大街的图上长度与光华大街的图上长度分别是16cm,10cm.
(1)新安大街与光华大街的实际长度各是多少米?
(2)新安大街与光华大街的图上长度之比是多少?
它们的实际长度之比呢?①、比例尺是指在地图或工程图纸上,图上长度
与实际长度的比.
②、本题中要注意单位的换算.注意:解(1)根据题意,得因此,新安大街的实际长度是:16×9000=144000(cm), 144000cm=1440m;
光华大街的实际长度是10 ×9000=90000 (cm)
90000cm=900m.(2)新安大街与光华大街的图上长度之比是
16:10=8:5;
新安大街与光华大街的实际长度之比是
144000:90000=8:5. *由上面的结果可以发现: *由此可见,实际长度之比等于图上长度之比,这一结论以后可以直接使用.在比例尺为1:8000的学校地图上,矩形运动场的图上尺寸是1cm×2cm,矩形运动场的实际尺寸是多少?解:根据题意,得因此,矩形运动场的长为: 2×8000=16000(cm) 16000cm=160m 矩形运动场的宽为: 1×8000= 8000(cm) 8000cm=80m1、你有什么收获?
2、学习线段比时应注意什么?1)两条线段的长度必须用同一单位表示;
2)两条线段的比没有单位(与采用的单位无关系),是一个正数;
3)两条线段的比的表示方法.课堂小结比例尺的概念比例尺——图上长度与实际长度的比.两条线段的比挑战自我:3.在RtΔABC中 ,AC=8,斜边BC=10,则ΔABC中的最短边与最长边的比值是__________1.画在图纸上的某一零件的长是32mm,如果比例尺是1:20,则该零件的实际长度为 ( )
A.1.6mm B. 640mm C.1.5mm D.608mm2.在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,则矩形运动场的实际尺寸是_______________4.等腰RtΔABC的斜边与直角边之比是_______B长160 m,宽80m3:55.如图中,甲,乙,丙三个矩形中,长与宽的比分别是多少?请判断哪两个矩形的长和宽的比是相等的?68484.56甲乙丙解:图甲的长和宽的比是8:6=4:3
图乙的长和宽的比是8:4=2:1
图丙的长和宽的比是6:4.5=4:3
由此可知:图甲与图丙的长和宽的比是相等的.即8:6=6:4.5挑战自我
即7.52:1.6=752:160(1)两条线段的比:如果选用同一个长度单位,量得两
条线段AB,CD的长度分别是m,n,那么就说这两条线段的
比AB:CD=m:n,或写成 其中,线段AB,CD分别叫
做这个线段比的前项和后项.(2)引入比值k的表示方法:如果把 表示成比值k,
那么 ,或 AB=k·CD.注意:引入比值k的方法是解决比例问题的一种重要方法,以后经常会用到. 练习1:已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b.解:a :b = 320 :120 = 8 :3或: 练习2:在Rt△ABC中,∠C=90°, CD是AB边的中线,求CD :AB.解:CD:AB = 1 :2D课内练习 例1:在某市城区地图(比例尺是1:9000)上,新安大街的图上长度与光华大街的图上长度分别是16cm,10cm.
(1)新安大街与光华大街的实际长度各是多少米?
(2)新安大街与光华大街的图上长度之比是多少?
它们的实际长度之比呢?①、比例尺是指在地图或工程图纸上,图上长度
与实际长度的比.
②、本题中要注意单位的换算.注意:解(1)根据题意,得因此,新安大街的实际长度是:16×9000=144000(cm), 144000cm=1440m;
光华大街的实际长度是10 ×9000=90000 (cm)
90000cm=900m.(2)新安大街与光华大街的图上长度之比是
16:10=8:5;
新安大街与光华大街的实际长度之比是
144000:90000=8:5. *由上面的结果可以发现: *由此可见,实际长度之比等于图上长度之比,这一结论以后可以直接使用.在比例尺为1:8000的学校地图上,矩形运动场的图上尺寸是1cm×2cm,矩形运动场的实际尺寸是多少?解:根据题意,得因此,矩形运动场的长为: 2×8000=16000(cm) 16000cm=160m 矩形运动场的宽为: 1×8000= 8000(cm) 8000cm=80m1、你有什么收获?
2、学习线段比时应注意什么?1)两条线段的长度必须用同一单位表示;
2)两条线段的比没有单位(与采用的单位无关系),是一个正数;
3)两条线段的比的表示方法.课堂小结比例尺的概念比例尺——图上长度与实际长度的比.两条线段的比挑战自我:3.在RtΔABC中 ,AC=8,斜边BC=10,则ΔABC中的最短边与最长边的比值是__________1.画在图纸上的某一零件的长是32mm,如果比例尺是1:20,则该零件的实际长度为 ( )
A.1.6mm B. 640mm C.1.5mm D.608mm2.在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,则矩形运动场的实际尺寸是_______________4.等腰RtΔABC的斜边与直角边之比是_______B长160 m,宽80m3:55.如图中,甲,乙,丙三个矩形中,长与宽的比分别是多少?请判断哪两个矩形的长和宽的比是相等的?68484.56甲乙丙解:图甲的长和宽的比是8:6=4:3
图乙的长和宽的比是8:4=2:1
图丙的长和宽的比是6:4.5=4:3
由此可知:图甲与图丙的长和宽的比是相等的.即8:6=6:4.5挑战自我
