2023-2024学年人教版数学八年级上册第十一章 三角形 单元知识链接(含解析)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册第十一章 三角形 单元知识链接(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 08:29:22 | ||
图片预览



文档简介
第十一章 三角形
【单元学习目标】
1.理解三角形及其内角、高、中线、角平分线等概念,了解三角形的分类,会画任意三角形的高、中线、角平分线.
2.理解三角形三边之间的关系并会证明,能利用该关系判断已知线段能否组成三角形.
3.会运用平行线的性质与平角的定义证明三角形三个内角和等于180°.
4.掌握“直角三角形的两个锐角互余”“有两个角互余的三角形是直角三角形”.
5.理解三角形外角的概念,掌握三角形外角的性质,并会运用三角形内角和定理及其外角性质进行相关计算和证明.
6.掌握多边形的内角和与外角和公式,能灵活运用多边形的内角和与外角和公式解决有关问题.
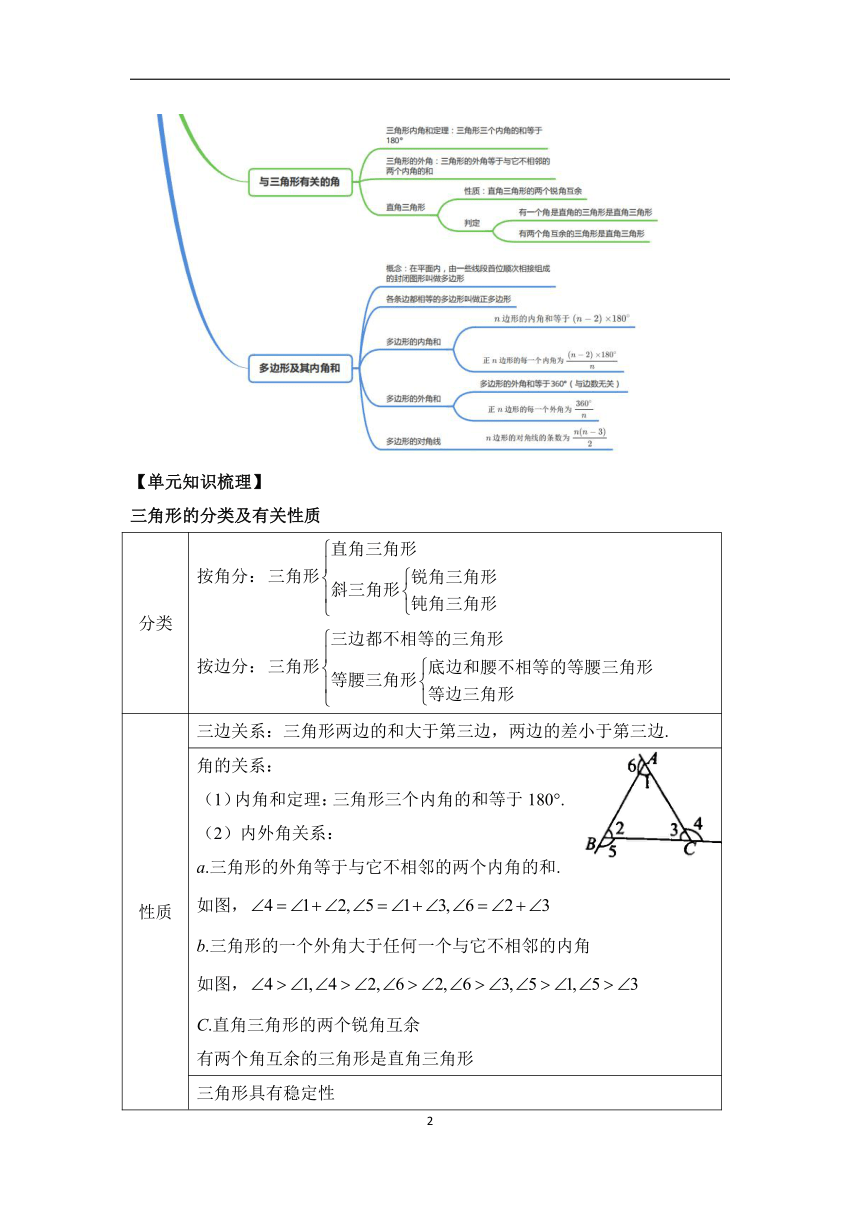
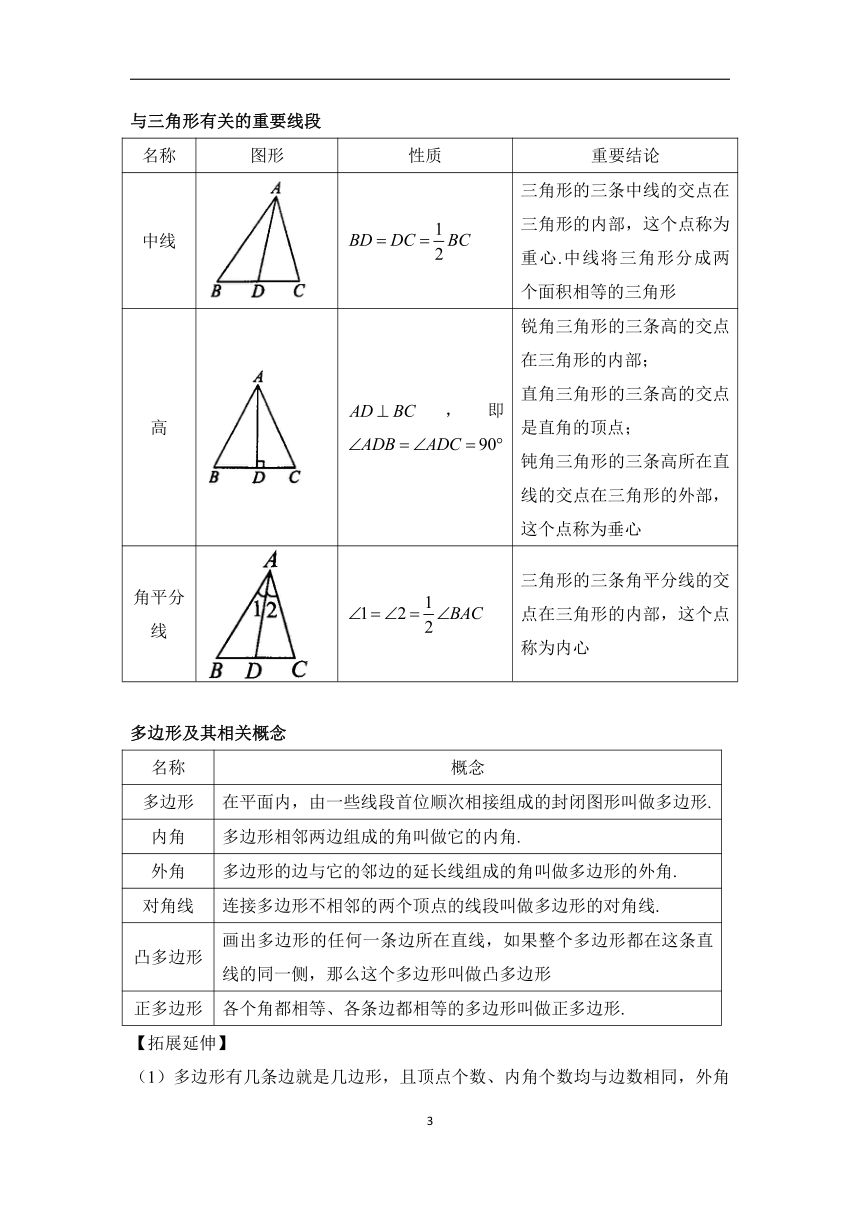
【单元思维导图】
【单元知识梳理】
三角形的分类及有关性质
分类 按角分: 按边分:
性质 三边关系:三角形两边的和大于第三边,两边的差小于第三边.
角的关系: (1)内角和定理:三角形三个内角的和等于180°. (2)内外角关系: a.三角形的外角等于与它不相邻的两个内角的和. 如图, b.三角形的一个外角大于任何一个与它不相邻的内角 如图, C.直角三角形的两个锐角互余 有两个角互余的三角形是直角三角形
三角形具有稳定性
与三角形有关的重要线段
名称 图形 性质 重要结论
中线 三角形的三条中线的交点在三角形的内部,这个点称为重心.中线将三角形分成两个面积相等的三角形
高 ,即 锐角三角形的三条高的交点在三角形的内部; 直角三角形的三条高的交点是直角的顶点; 钝角三角形的三条高所在直线的交点在三角形的外部,这个点称为垂心
角平分线 三角形的三条角平分线的交点在三角形的内部,这个点称为内心
多边形及其相关概念
名称 概念
多边形 在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形.
内角 多边形相邻两边组成的角叫做它的内角.
外角 多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线 连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
凸多边形 画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形叫做凸多边形
正多边形 各个角都相等、各条边都相等的多边形叫做正多边形.
【拓展延伸】
(1)多边形有几条边就是几边形,且顶点个数、内角个数均与边数相同,外角个数是边数的2倍.
(2)从边形的一个顶点可以引出条对角线,引出的对角线将边形分成个三角形,边形有个顶点,共有条对角线.
【易错点津】
(1)三角形没有对角线.
(2)正多边形必须满足定义中的两个条件:①各个角都相等;②各条边都相等.二者不可缺一.如果一个多边形的各个角都相等或每条边都相等,那么这个多边形不一定是正多边形,如长方形.
多边形的内角和
内容 推理过程 应用
方法 图形
边形内角和等于 . 方法1:如图所示,从边形的一个顶点引出条对角线,这条对角线把边形分成个三角形,每个三角形的内角和是,所以变形的内角和是. (1)已知边数,求内角和. (2)已知内角和,求边数. (3)已知正边形每个内角的度数.求边数和内角和.
方法2:如图所示,在边形内任取一点P,连接,把边形分成个三角形,这个三角形的内角和为,再减去一个周角,即得边形的内角和是.
方法3:如图所示,在边形的一边上任取一点P与各顶点相连,得个三角形,边形内角和等于这个三角形的内角和减去在点P处的一个平角,即.
【拓展延伸】
利用多边形的内角和公式求边数(此类题都隐含着边数为正整数这个条件),相当于解一元一次方程.
【规律方法】
(1)多边形内角和公式的推理过程是将多边形的内角进行分割,然后把它们放到三角形中,随着点P的位置不同所得三角形个数也不同,但以上几种证明方法都是把多边形的问题转化为三角形的问题进行解决.
(2)任意多边形的内角和是的整数倍,且多边形每增加一条边,它的内角和就增加,正边形每个内角的度数是.
多边形的外角和
内容 推导过程 应用
多边形的外角和等于 多边的每个内角和与它相邻的外角都是邻补角,所以边形的内角和加上外角和为,外角和等于 (1)已知外角度数求正多边形的边数. (2)已知正多边形的边数求外角度数.
【拓展延伸】
(1)多边形的外角和恒等于,与边数多少无关.
(2)正边形的每个内角都相等,则每个外角也相等,其外角和为,所以正变形的每个外角度数都为.
(3)正多边形的内角相等,隐含着外角也相等这一条件,利用这种隐含关系求正多边形的边数比直接利用内角和求边数要简单.
(4)添加:根据多边形外角和是可推得多边形的外角中最多有三个钝角,与之对应,多边形的内角中最多有三个锐角.
【单元常考题型】
题型1 三角形三边关系的应用
①判断已知的三条线段能否组成三角形
1.以下列各组线段的长为边能组成三角形的是( )
A.2、5、8 B.2、5、3 C.6、6、2 D.9、6、2
②与等腰三角形周长(或边长)有关的计算
2.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
③利用三角形的三边关系进行化简
3.已知a,b,c是的三边,化简:______.
题型2 与三角形的高有关的计算
4.如图,,垂足为B,,垂足为C,且AC与BD交于点E.
(1)的边DE上的高为___________,边AE上的高为_________.
(2)若E是BD的中点,,,,求AB的长.
题型3 与三角形的中线有关的计算
①与三角形中线有关的面积问题
5.如图,AD是的中线,CE是的中线,,则_____.
②与三角形中线有关的周长问题(易错)
6.等腰三角形一腰上的中线.将等腰三角形的周长分为24cm和12cm两部分,求这个等腰三角形的底边长.
题型4利用三角形的内角和或外角的性质求角度——一题多解
7.如图,CE是的外角的平分线,且CE交BA的延长线于点E.
(1)若,,求的度数;
(2)求证:.
题型5直角三角形的性质与判定的应用
8.中,,,点D在线段BC上,若为直角三角形时的度数为( )
A. B. C.或 D.或
题型6三角形内角和定理的应用
9.如图,在中,,,AE平分交BC于点E.P是边BC上的动点(不与B,C重合),连接AP,将沿AP翻折得到,连接DC,记.
(1)如图,当P与E重合时,求的度数.
(2)当P与E不重合时,记,探究与的数量关系.
题型7三角形外角的性质在实际问题中的应用
10.每周我们都举行升旗仪式,你是否想到其中也有数学问题?国旗中有5个五角星,每个五角星的五个角的度数之和是一个定值,这个值是( )
A. B. C. D.
题型8利用内、外角和公式求边数
11.已知正多边形的一个内角是135°,则这个正多边形的边数是( )
A.3 B.4 C.6 D.8
题型9利用内、外角和公式求角度
12.2022 年北京冬奥会开幕式为世界奉献了一场精彩,简约,唯美,浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A. B. C. D.
题型10 多边形对角线公式的应用(易错)
13.一个多边形的内角和为540°,则它的对角线共有( )
A.3条 B.5条 C.6条 D.12条
题型11 多边形的截角问题(易错)
14.若一个多边形截去一个角后,形成的新多边形的内角和是,则原来多边形的边数可能是( )
A.10或11 B.11 C.11或12 D.10或11或12
【单元对接中考】
1.【2023.湖南长沙】下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D. 3,3,6
2.【2023.北京】正十二边形的外角和为( )
A. B. C. D.
3.【2023.山西】如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若,,则的度数为( )
A. B. C. D.
4.【2023.福建】若某三角形的三边长分别为3,4,m,则m的值可以是( )
A.1 B.5 C.7 D.9
5.【2023.江西】如图,平面镜MN放置在水平地面CD上,墙面于点D,一束光线AO照射到镜面MN上,反射光线为OB,点B在PD上,若,则的度数为( )
A. B. C. D.
6.【2023.湖北黄冈】如图,的直角顶点A在直线a上,斜边BC在直线b上,若,,则( )
A. B. C. D.
7.【2023.甘肃兰州】如图(1)是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图(2)是八角形空窗的示意图,它的一个外角( )
A. B. C. D.
8.【2023.吉林】如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________.
9.【2023.江苏扬州】如果一个多边形每一个外角都是,那么这个多边形的边数为________.
10.【2023.重庆A】如图,在正五边形ABCDE中,连接AC,那么的度数为________.
11.【2023.山东济宁】一个多边形的内角和为540°,则这个多边形是_________边形.
12.【2023.吉林长春】如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点的对应点为点,折痕为AF,则的大小为__________度.
13.【2023.江苏连云港】如图,以正六边形ABCDEF的顶点C为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线BC上,则正六边形ABCDEF至少旋转________°.
答案以及解析
【单元常考题型】
1.答案:C
解析:根据三角形任意两边的和大于第三边,可知:
A、,不能够组成三角形,故不符合题意;
B、,不能组成三角形,故不符合题意;
C、,能组成三角形,故符合题意;
D、,不能组成三角形,故不符合题意;
故选C.
2.答案:B
解析:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:,而,不满足三角形的三边关系;
故底边长是:3cm.故选B.
3.答案:.
解析:的三边长分别是a、b、c,
,,,
.
4.答案:(1)AB;DC
(2)
解析:(1)略
(2)边DE上的高为AB,边AE上的高为DC,
.
,,,
,.
5.答案:12
解析:CE是的中线,
.
AD是的中线,
.
故答案为:12.
6.答案:4cm
解析:设这个等腰三角形的腰长为2xcm,底边长为ycm,
依题意得:或,
解得:或,
①当时,三边长为16cm,16cm,4cm.符合三角形三边关系;
②当时,三边长为8cm,8cm,20cm.因为,故不符合三角形三边关系,应舍去.
答:等腰三角形的底边长为4cm.
7.答案:(1)84°
(2)见解析
解析:(1),,
.
CE平分,
,
,
即.
(2)证明:CE平分,
.
,
.
,
,
.
8.答案:D
解析:在中,,,
,
点D在BC边上,为直角三角形,
如图1,
当时,则,
如图2,
图2
当时,则.
综上所述,的度数是或.
故选:D.
9.(1)答案:
解析:,,
.
平分,
.
P与E重合,
点D在AB边上,,
,
.
(2)答案:或
解析:①如图(1),当点P在线段BE上时,
由题意知,,
.
又,
,
.
②如图(2),当点P在线段CE上时,
延长AD交BC于点F,
易知.
,
,
.
10.答案:A
解析:如图,
是的外角,,
是的外角,,
,
.
故选A.
11.答案:D
解析:正多边形的一个内角是135°,
该正多边形的一个外角为45°,
多边形的外角之和为360°,
边数,
这个正多边形的边数是8.
故选D.
12.答案:C
解析:,
,
答:一个六边形的每个内角的度数是.
故选C.
13.答案:B
解析:设该多边形的边数为n,,解得,这个多边形共有条对角线.故选B.
14.答案:D
解析:设新多边形的边数为n,则,解得.多边形截去一个角后,边数可以增加1、不变或减少1,原来多边形的边数可能是10或11或12.故选D.
【单元对接中考】
1.答案:C
解析:根据三角形三边关系:两边之差<第三边<两边之和,可知选C.
2.答案:C
3.答案:C
解析:由平行线的性质知.又,.
4.答案:B
解析:由三角形三边之间的大小关系可知,,,故选B.
5.答案:C
解析:如图,过点O作,则.又,.又,.故选C.
6.答案:C
解析:,.,.
7.答案:A
8.答案:三角形具有稳定性
9.答案:6
解析:因为这个多边形的每一个外角都是,所以这个多边形是一个正多边形.设该正多边形的边数为n,根据多边形的外角和为,可知,所以.
10.答案:36°
解析:正五边形的内角和为,,.
11.答案:五
解析:设这个多边形有n条边,由题意得,,解得.
12.答案:45
解析:正五边形的每个内角为,,,.
13.答案:60
解析:正六边形的每一个外角的度数为,要使点落在直线BC上,则正六边形ABCDEF至少旋转.
2
【单元学习目标】
1.理解三角形及其内角、高、中线、角平分线等概念,了解三角形的分类,会画任意三角形的高、中线、角平分线.
2.理解三角形三边之间的关系并会证明,能利用该关系判断已知线段能否组成三角形.
3.会运用平行线的性质与平角的定义证明三角形三个内角和等于180°.
4.掌握“直角三角形的两个锐角互余”“有两个角互余的三角形是直角三角形”.
5.理解三角形外角的概念,掌握三角形外角的性质,并会运用三角形内角和定理及其外角性质进行相关计算和证明.
6.掌握多边形的内角和与外角和公式,能灵活运用多边形的内角和与外角和公式解决有关问题.
【单元思维导图】
【单元知识梳理】
三角形的分类及有关性质
分类 按角分: 按边分:
性质 三边关系:三角形两边的和大于第三边,两边的差小于第三边.
角的关系: (1)内角和定理:三角形三个内角的和等于180°. (2)内外角关系: a.三角形的外角等于与它不相邻的两个内角的和. 如图, b.三角形的一个外角大于任何一个与它不相邻的内角 如图, C.直角三角形的两个锐角互余 有两个角互余的三角形是直角三角形
三角形具有稳定性
与三角形有关的重要线段
名称 图形 性质 重要结论
中线 三角形的三条中线的交点在三角形的内部,这个点称为重心.中线将三角形分成两个面积相等的三角形
高 ,即 锐角三角形的三条高的交点在三角形的内部; 直角三角形的三条高的交点是直角的顶点; 钝角三角形的三条高所在直线的交点在三角形的外部,这个点称为垂心
角平分线 三角形的三条角平分线的交点在三角形的内部,这个点称为内心
多边形及其相关概念
名称 概念
多边形 在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形.
内角 多边形相邻两边组成的角叫做它的内角.
外角 多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线 连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
凸多边形 画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形叫做凸多边形
正多边形 各个角都相等、各条边都相等的多边形叫做正多边形.
【拓展延伸】
(1)多边形有几条边就是几边形,且顶点个数、内角个数均与边数相同,外角个数是边数的2倍.
(2)从边形的一个顶点可以引出条对角线,引出的对角线将边形分成个三角形,边形有个顶点,共有条对角线.
【易错点津】
(1)三角形没有对角线.
(2)正多边形必须满足定义中的两个条件:①各个角都相等;②各条边都相等.二者不可缺一.如果一个多边形的各个角都相等或每条边都相等,那么这个多边形不一定是正多边形,如长方形.
多边形的内角和
内容 推理过程 应用
方法 图形
边形内角和等于 . 方法1:如图所示,从边形的一个顶点引出条对角线,这条对角线把边形分成个三角形,每个三角形的内角和是,所以变形的内角和是. (1)已知边数,求内角和. (2)已知内角和,求边数. (3)已知正边形每个内角的度数.求边数和内角和.
方法2:如图所示,在边形内任取一点P,连接,把边形分成个三角形,这个三角形的内角和为,再减去一个周角,即得边形的内角和是.
方法3:如图所示,在边形的一边上任取一点P与各顶点相连,得个三角形,边形内角和等于这个三角形的内角和减去在点P处的一个平角,即.
【拓展延伸】
利用多边形的内角和公式求边数(此类题都隐含着边数为正整数这个条件),相当于解一元一次方程.
【规律方法】
(1)多边形内角和公式的推理过程是将多边形的内角进行分割,然后把它们放到三角形中,随着点P的位置不同所得三角形个数也不同,但以上几种证明方法都是把多边形的问题转化为三角形的问题进行解决.
(2)任意多边形的内角和是的整数倍,且多边形每增加一条边,它的内角和就增加,正边形每个内角的度数是.
多边形的外角和
内容 推导过程 应用
多边形的外角和等于 多边的每个内角和与它相邻的外角都是邻补角,所以边形的内角和加上外角和为,外角和等于 (1)已知外角度数求正多边形的边数. (2)已知正多边形的边数求外角度数.
【拓展延伸】
(1)多边形的外角和恒等于,与边数多少无关.
(2)正边形的每个内角都相等,则每个外角也相等,其外角和为,所以正变形的每个外角度数都为.
(3)正多边形的内角相等,隐含着外角也相等这一条件,利用这种隐含关系求正多边形的边数比直接利用内角和求边数要简单.
(4)添加:根据多边形外角和是可推得多边形的外角中最多有三个钝角,与之对应,多边形的内角中最多有三个锐角.
【单元常考题型】
题型1 三角形三边关系的应用
①判断已知的三条线段能否组成三角形
1.以下列各组线段的长为边能组成三角形的是( )
A.2、5、8 B.2、5、3 C.6、6、2 D.9、6、2
②与等腰三角形周长(或边长)有关的计算
2.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
③利用三角形的三边关系进行化简
3.已知a,b,c是的三边,化简:______.
题型2 与三角形的高有关的计算
4.如图,,垂足为B,,垂足为C,且AC与BD交于点E.
(1)的边DE上的高为___________,边AE上的高为_________.
(2)若E是BD的中点,,,,求AB的长.
题型3 与三角形的中线有关的计算
①与三角形中线有关的面积问题
5.如图,AD是的中线,CE是的中线,,则_____.
②与三角形中线有关的周长问题(易错)
6.等腰三角形一腰上的中线.将等腰三角形的周长分为24cm和12cm两部分,求这个等腰三角形的底边长.
题型4利用三角形的内角和或外角的性质求角度——一题多解
7.如图,CE是的外角的平分线,且CE交BA的延长线于点E.
(1)若,,求的度数;
(2)求证:.
题型5直角三角形的性质与判定的应用
8.中,,,点D在线段BC上,若为直角三角形时的度数为( )
A. B. C.或 D.或
题型6三角形内角和定理的应用
9.如图,在中,,,AE平分交BC于点E.P是边BC上的动点(不与B,C重合),连接AP,将沿AP翻折得到,连接DC,记.
(1)如图,当P与E重合时,求的度数.
(2)当P与E不重合时,记,探究与的数量关系.
题型7三角形外角的性质在实际问题中的应用
10.每周我们都举行升旗仪式,你是否想到其中也有数学问题?国旗中有5个五角星,每个五角星的五个角的度数之和是一个定值,这个值是( )
A. B. C. D.
题型8利用内、外角和公式求边数
11.已知正多边形的一个内角是135°,则这个正多边形的边数是( )
A.3 B.4 C.6 D.8
题型9利用内、外角和公式求角度
12.2022 年北京冬奥会开幕式为世界奉献了一场精彩,简约,唯美,浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A. B. C. D.
题型10 多边形对角线公式的应用(易错)
13.一个多边形的内角和为540°,则它的对角线共有( )
A.3条 B.5条 C.6条 D.12条
题型11 多边形的截角问题(易错)
14.若一个多边形截去一个角后,形成的新多边形的内角和是,则原来多边形的边数可能是( )
A.10或11 B.11 C.11或12 D.10或11或12
【单元对接中考】
1.【2023.湖南长沙】下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D. 3,3,6
2.【2023.北京】正十二边形的外角和为( )
A. B. C. D.
3.【2023.山西】如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若,,则的度数为( )
A. B. C. D.
4.【2023.福建】若某三角形的三边长分别为3,4,m,则m的值可以是( )
A.1 B.5 C.7 D.9
5.【2023.江西】如图,平面镜MN放置在水平地面CD上,墙面于点D,一束光线AO照射到镜面MN上,反射光线为OB,点B在PD上,若,则的度数为( )
A. B. C. D.
6.【2023.湖北黄冈】如图,的直角顶点A在直线a上,斜边BC在直线b上,若,,则( )
A. B. C. D.
7.【2023.甘肃兰州】如图(1)是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图(2)是八角形空窗的示意图,它的一个外角( )
A. B. C. D.
8.【2023.吉林】如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________.
9.【2023.江苏扬州】如果一个多边形每一个外角都是,那么这个多边形的边数为________.
10.【2023.重庆A】如图,在正五边形ABCDE中,连接AC,那么的度数为________.
11.【2023.山东济宁】一个多边形的内角和为540°,则这个多边形是_________边形.
12.【2023.吉林长春】如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点的对应点为点,折痕为AF,则的大小为__________度.
13.【2023.江苏连云港】如图,以正六边形ABCDEF的顶点C为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线BC上,则正六边形ABCDEF至少旋转________°.
答案以及解析
【单元常考题型】
1.答案:C
解析:根据三角形任意两边的和大于第三边,可知:
A、,不能够组成三角形,故不符合题意;
B、,不能组成三角形,故不符合题意;
C、,能组成三角形,故符合题意;
D、,不能组成三角形,故不符合题意;
故选C.
2.答案:B
解析:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:,而,不满足三角形的三边关系;
故底边长是:3cm.故选B.
3.答案:.
解析:的三边长分别是a、b、c,
,,,
.
4.答案:(1)AB;DC
(2)
解析:(1)略
(2)边DE上的高为AB,边AE上的高为DC,
.
,,,
,.
5.答案:12
解析:CE是的中线,
.
AD是的中线,
.
故答案为:12.
6.答案:4cm
解析:设这个等腰三角形的腰长为2xcm,底边长为ycm,
依题意得:或,
解得:或,
①当时,三边长为16cm,16cm,4cm.符合三角形三边关系;
②当时,三边长为8cm,8cm,20cm.因为,故不符合三角形三边关系,应舍去.
答:等腰三角形的底边长为4cm.
7.答案:(1)84°
(2)见解析
解析:(1),,
.
CE平分,
,
,
即.
(2)证明:CE平分,
.
,
.
,
,
.
8.答案:D
解析:在中,,,
,
点D在BC边上,为直角三角形,
如图1,
当时,则,
如图2,
图2
当时,则.
综上所述,的度数是或.
故选:D.
9.(1)答案:
解析:,,
.
平分,
.
P与E重合,
点D在AB边上,,
,
.
(2)答案:或
解析:①如图(1),当点P在线段BE上时,
由题意知,,
.
又,
,
.
②如图(2),当点P在线段CE上时,
延长AD交BC于点F,
易知.
,
,
.
10.答案:A
解析:如图,
是的外角,,
是的外角,,
,
.
故选A.
11.答案:D
解析:正多边形的一个内角是135°,
该正多边形的一个外角为45°,
多边形的外角之和为360°,
边数,
这个正多边形的边数是8.
故选D.
12.答案:C
解析:,
,
答:一个六边形的每个内角的度数是.
故选C.
13.答案:B
解析:设该多边形的边数为n,,解得,这个多边形共有条对角线.故选B.
14.答案:D
解析:设新多边形的边数为n,则,解得.多边形截去一个角后,边数可以增加1、不变或减少1,原来多边形的边数可能是10或11或12.故选D.
【单元对接中考】
1.答案:C
解析:根据三角形三边关系:两边之差<第三边<两边之和,可知选C.
2.答案:C
3.答案:C
解析:由平行线的性质知.又,.
4.答案:B
解析:由三角形三边之间的大小关系可知,,,故选B.
5.答案:C
解析:如图,过点O作,则.又,.又,.故选C.
6.答案:C
解析:,.,.
7.答案:A
8.答案:三角形具有稳定性
9.答案:6
解析:因为这个多边形的每一个外角都是,所以这个多边形是一个正多边形.设该正多边形的边数为n,根据多边形的外角和为,可知,所以.
10.答案:36°
解析:正五边形的内角和为,,.
11.答案:五
解析:设这个多边形有n条边,由题意得,,解得.
12.答案:45
解析:正五边形的每个内角为,,,.
13.答案:60
解析:正六边形的每一个外角的度数为,要使点落在直线BC上,则正六边形ABCDEF至少旋转.
2
