2008届黑龙江省西北部地区八校高三第二次联考数学理科试卷(含答案)(黑龙江省齐齐哈尔市)
文档属性
| 名称 | 2008届黑龙江省西北部地区八校高三第二次联考数学理科试卷(含答案)(黑龙江省齐齐哈尔市) |

|
|
| 格式 | rar | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-21 15:20:00 | ||
图片预览



文档简介
2008届黑龙江省西北部地区八校高三联考
数学试卷(理科)
一、选择题
1. 已知全集U={0,1,2},且CuA={2},则集合A的真子集共有
A 3个 B 4个 C 5个 D 6个
2、已知i是虚数单位,则等于
A B C 1+I D 1-i
3、已知直线a、b、c和平面、,有下列命题:(1)若,a,则a;(2)若ab,a,b,则;(3)若, a,则a;(4)若a,,则a。其中正确的命题有
A (1)(2) B (1)(3) C (2)(4) D (2)
4、如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差的变化情况是
A 平均数和方差都不变 B平均数不变,方差改变
C 平均数改变,方差不变 D平均数和方差都改变
5、设等差数列{an}的前n项和为Sn ,且a2,a4是方程x2-x-2=0的两个根,则S5等于
A B 5 C D -5
6、已知A、B、C是平面上不共线的三点,O为ABC的外心,D是AB的中点,动点P满足,则动点P的轨迹一定过ABC的
A 内心 B 外心 C 重心 D 垂心
7、连续抛掷一颗骰子两次,分别得到点数m、n,记向量(m,n)与向量(-1,1)的夹角为,则的概率是
A B C D
8、已知点P(x,y)在不等式组表示的平面区域上运动,则的取值范围是
A B C D
9、在算式“”的两个、中,分别填入两个正整数,使它们的倒数之和最小,则这两个数构成的数对(、)应为
A (4,14) B (6,6) C (3,18) D (5,10)
10、设函数, 则
A 在区间上是增函数 B 在区间上是增函数
C在区间上是增函数 D在区间上是增函数
11、已知双曲线的左、右焦点分别为F1、F2,P是准线上一点,且PF1PF2,,则双曲线的离心率是
A B C 2 D 3
12、已知定义在R上的函数为奇函数,且函数的周期为3,若,则的值为
A 0 B 5 C 2 D -5
二、填空题
13、在ABC中,角A、B、C的对边分别为a、b、c,若,c=4,b=,则ABC的面积为_____________________________
14、设是定义在R上的奇函数,在上有且,则不等式的解集为_____________________________
15、已知抛物线(p为常数,)上不同两点A、B的横坐标恰好是关于x的方程(q为常数)的两个根,则直线AB的方程为_______________________
16、给出下列四个命题:
(1)当
(2)圆上任意一点M关于直线ax-y-5a-2=0的对称点在该圆上
(3)若函数的图像关于x=1对称,则为偶函数
(4)若的值为2
其中正确命题的序号为____________________________
三、解答题
17.(本小题满分10分)
已知向量,函数且a为常数)
(1)若求的最小正周期;
(2)当时,的最小值为4,求a的值
18. (本小题满分12分)
在一次有奖竞猜活动中,有A、B两个相互独立的问题,现规定:答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题可自由选择,但只有第一个问题答对,才能再答第二个问题,否则终止答题。若你参加答题,且假设答对问题A、B的概率分别为、
(!)记先回答问题A获得的奖金数为随机变量,则的可能取值分别是多少?
(2)先回答哪个问题才能使你获得更多的奖金?请说明理由。
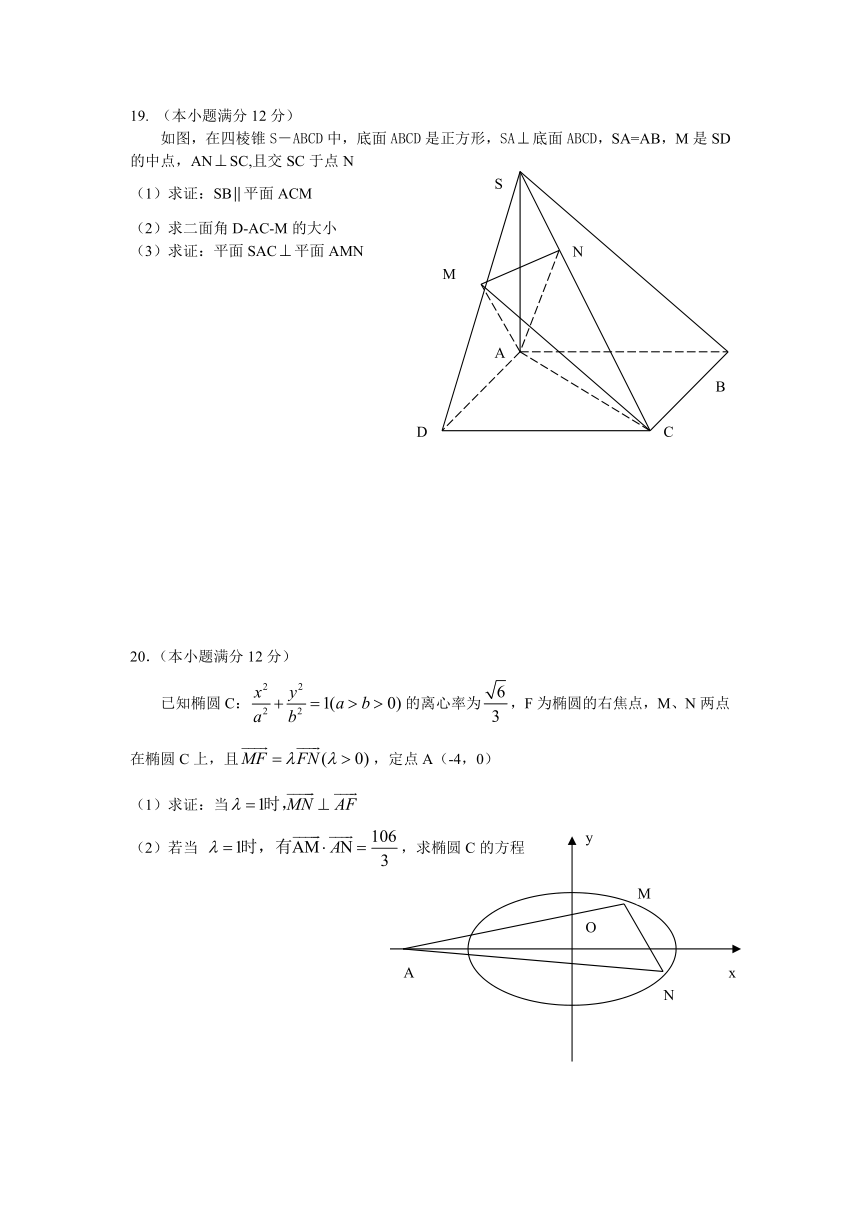
19. (本小题满分12分)
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA底面ABCD,SA=AB,M是SD的中点,ANSC,且交SC于点N
(1)求证:SB平面ACM
(2)求二面角D-AC-M的大小
(3)求证:平面SAC平面AMN
20.(本小题满分12分)
已知椭圆C:的离心率为,F为椭圆的右焦点,M、N两点在椭圆C上,且,定点A(-4,0)
(1)求证:当
(2)若当 ,求椭圆C的方程
21. (本小题满分12分)
已知点列M1(x1,1),M2(x2,2),…,且与向量垂直,其中c是不等于零的是常数,n是正整数,设x1=1,求数列的通项公式,并求其前n项和
22. (本小题满分12分)
设函数
(1)求函数的极值点
(2)当时,若对任意的,恒有,求的取值范围
(3)证明:
2008届黑龙江省西北部地区八校高三联考
数学试卷(理科)答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
C
A
C
D
D
D
A
B
B
13. 14.
15. 16. (2)、(3)、(4)
17. (本小题满分10分)
解:
……………………………………5分
(2)
…………………10分
18. (本小题满分12分)
解:(1)随机变量的可能取值分别为0,1000,3000
(2)设先回答问题A获得的奖金为元,先回答问题B获得的奖金为元,则有
……………………7分
同理:
…………………11分
故先回答问题A获得的奖金期望较多。 ……………………………12分
19. (本小题满分12分)
(1)证明:连结BD交AC于E,连结ME
ABCD是正方形 E是BD的中点
M是SD的中点 ME是DSB的中位线 MESB
又ME平面ACM,SB平面ACM SB平面ACM …………………4分
(2)解:?取AD的中点F,则MFSA,作FQAC于Q,连结MQ
SA平面ABCD
MF平面ABCD
FQ为MQ在平面ABCD内的射影
FQAC MQAC
FQM为二面角D-AC-M的平面角
设SA=AB=a,在RtMFQ中,
MF=SA=,FQ=DE=
tanFQM=
二面角D-AC-M的大小为arctan ………………………………8分
(3)证明:由条件有DCSA,DCDA,DC平面SAD,AMDC
又SA=AD,M是SD的中点,AMSD
AM平面SDC SCAM,由已知SCAN, SC平面AMN
又SC平面SAC平面SAC平面AMN …………………………………12分
20. (本小题满分12分)
解:(1)设M(x1,y1)、N(x2,y2),F(c,0)
则
由M、N两点在椭圆上
…………………………………6分
(2)
又
………………………………………………12分
21. (本小题满分12分)
解:由题意得:
…………………………………3分
…………6分
当时,此时 …………………………8分
当时,
此时
= ………12分
22. (1)解: …1分
在上无极值点 ……………………………2分
当时,令,随x的变化情况如下表:
x
+
0
-
递增
极大值
递减
从上表可以看出,当时,有唯一的极大值点
(2)解:当时,在处取得极大值
此极大值也是最大值。
要使恒成立,只需
的取值范围是 …………………………………………………7分
(3)证明:令p=1,由(2)知:
…………………………………………………………9分
……………………………………………12分
数学试卷(理科)
一、选择题
1. 已知全集U={0,1,2},且CuA={2},则集合A的真子集共有
A 3个 B 4个 C 5个 D 6个
2、已知i是虚数单位,则等于
A B C 1+I D 1-i
3、已知直线a、b、c和平面、,有下列命题:(1)若,a,则a;(2)若ab,a,b,则;(3)若, a,则a;(4)若a,,则a。其中正确的命题有
A (1)(2) B (1)(3) C (2)(4) D (2)
4、如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差的变化情况是
A 平均数和方差都不变 B平均数不变,方差改变
C 平均数改变,方差不变 D平均数和方差都改变
5、设等差数列{an}的前n项和为Sn ,且a2,a4是方程x2-x-2=0的两个根,则S5等于
A B 5 C D -5
6、已知A、B、C是平面上不共线的三点,O为ABC的外心,D是AB的中点,动点P满足,则动点P的轨迹一定过ABC的
A 内心 B 外心 C 重心 D 垂心
7、连续抛掷一颗骰子两次,分别得到点数m、n,记向量(m,n)与向量(-1,1)的夹角为,则的概率是
A B C D
8、已知点P(x,y)在不等式组表示的平面区域上运动,则的取值范围是
A B C D
9、在算式“”的两个、中,分别填入两个正整数,使它们的倒数之和最小,则这两个数构成的数对(、)应为
A (4,14) B (6,6) C (3,18) D (5,10)
10、设函数, 则
A 在区间上是增函数 B 在区间上是增函数
C在区间上是增函数 D在区间上是增函数
11、已知双曲线的左、右焦点分别为F1、F2,P是准线上一点,且PF1PF2,,则双曲线的离心率是
A B C 2 D 3
12、已知定义在R上的函数为奇函数,且函数的周期为3,若,则的值为
A 0 B 5 C 2 D -5
二、填空题
13、在ABC中,角A、B、C的对边分别为a、b、c,若,c=4,b=,则ABC的面积为_____________________________
14、设是定义在R上的奇函数,在上有且,则不等式的解集为_____________________________
15、已知抛物线(p为常数,)上不同两点A、B的横坐标恰好是关于x的方程(q为常数)的两个根,则直线AB的方程为_______________________
16、给出下列四个命题:
(1)当
(2)圆上任意一点M关于直线ax-y-5a-2=0的对称点在该圆上
(3)若函数的图像关于x=1对称,则为偶函数
(4)若的值为2
其中正确命题的序号为____________________________
三、解答题
17.(本小题满分10分)
已知向量,函数且a为常数)
(1)若求的最小正周期;
(2)当时,的最小值为4,求a的值
18. (本小题满分12分)
在一次有奖竞猜活动中,有A、B两个相互独立的问题,现规定:答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题可自由选择,但只有第一个问题答对,才能再答第二个问题,否则终止答题。若你参加答题,且假设答对问题A、B的概率分别为、
(!)记先回答问题A获得的奖金数为随机变量,则的可能取值分别是多少?
(2)先回答哪个问题才能使你获得更多的奖金?请说明理由。
19. (本小题满分12分)
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA底面ABCD,SA=AB,M是SD的中点,ANSC,且交SC于点N
(1)求证:SB平面ACM
(2)求二面角D-AC-M的大小
(3)求证:平面SAC平面AMN
20.(本小题满分12分)
已知椭圆C:的离心率为,F为椭圆的右焦点,M、N两点在椭圆C上,且,定点A(-4,0)
(1)求证:当
(2)若当 ,求椭圆C的方程
21. (本小题满分12分)
已知点列M1(x1,1),M2(x2,2),…,且与向量垂直,其中c是不等于零的是常数,n是正整数,设x1=1,求数列的通项公式,并求其前n项和
22. (本小题满分12分)
设函数
(1)求函数的极值点
(2)当时,若对任意的,恒有,求的取值范围
(3)证明:
2008届黑龙江省西北部地区八校高三联考
数学试卷(理科)答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
C
A
C
D
D
D
A
B
B
13. 14.
15. 16. (2)、(3)、(4)
17. (本小题满分10分)
解:
……………………………………5分
(2)
…………………10分
18. (本小题满分12分)
解:(1)随机变量的可能取值分别为0,1000,3000
(2)设先回答问题A获得的奖金为元,先回答问题B获得的奖金为元,则有
……………………7分
同理:
…………………11分
故先回答问题A获得的奖金期望较多。 ……………………………12分
19. (本小题满分12分)
(1)证明:连结BD交AC于E,连结ME
ABCD是正方形 E是BD的中点
M是SD的中点 ME是DSB的中位线 MESB
又ME平面ACM,SB平面ACM SB平面ACM …………………4分
(2)解:?取AD的中点F,则MFSA,作FQAC于Q,连结MQ
SA平面ABCD
MF平面ABCD
FQ为MQ在平面ABCD内的射影
FQAC MQAC
FQM为二面角D-AC-M的平面角
设SA=AB=a,在RtMFQ中,
MF=SA=,FQ=DE=
tanFQM=
二面角D-AC-M的大小为arctan ………………………………8分
(3)证明:由条件有DCSA,DCDA,DC平面SAD,AMDC
又SA=AD,M是SD的中点,AMSD
AM平面SDC SCAM,由已知SCAN, SC平面AMN
又SC平面SAC平面SAC平面AMN …………………………………12分
20. (本小题满分12分)
解:(1)设M(x1,y1)、N(x2,y2),F(c,0)
则
由M、N两点在椭圆上
…………………………………6分
(2)
又
………………………………………………12分
21. (本小题满分12分)
解:由题意得:
…………………………………3分
…………6分
当时,此时 …………………………8分
当时,
此时
= ………12分
22. (1)解: …1分
在上无极值点 ……………………………2分
当时,令,随x的变化情况如下表:
x
+
0
-
递增
极大值
递减
从上表可以看出,当时,有唯一的极大值点
(2)解:当时,在处取得极大值
此极大值也是最大值。
要使恒成立,只需
的取值范围是 …………………………………………………7分
(3)证明:令p=1,由(2)知:
…………………………………………………………9分
……………………………………………12分
