24.1.2垂直于弦的直径强化训练(含答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2垂直于弦的直径强化训练(含答案)2023-2024学年人教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 00:00:00 | ||
图片预览


文档简介
24.1.2垂直于弦的直径
一、单选题
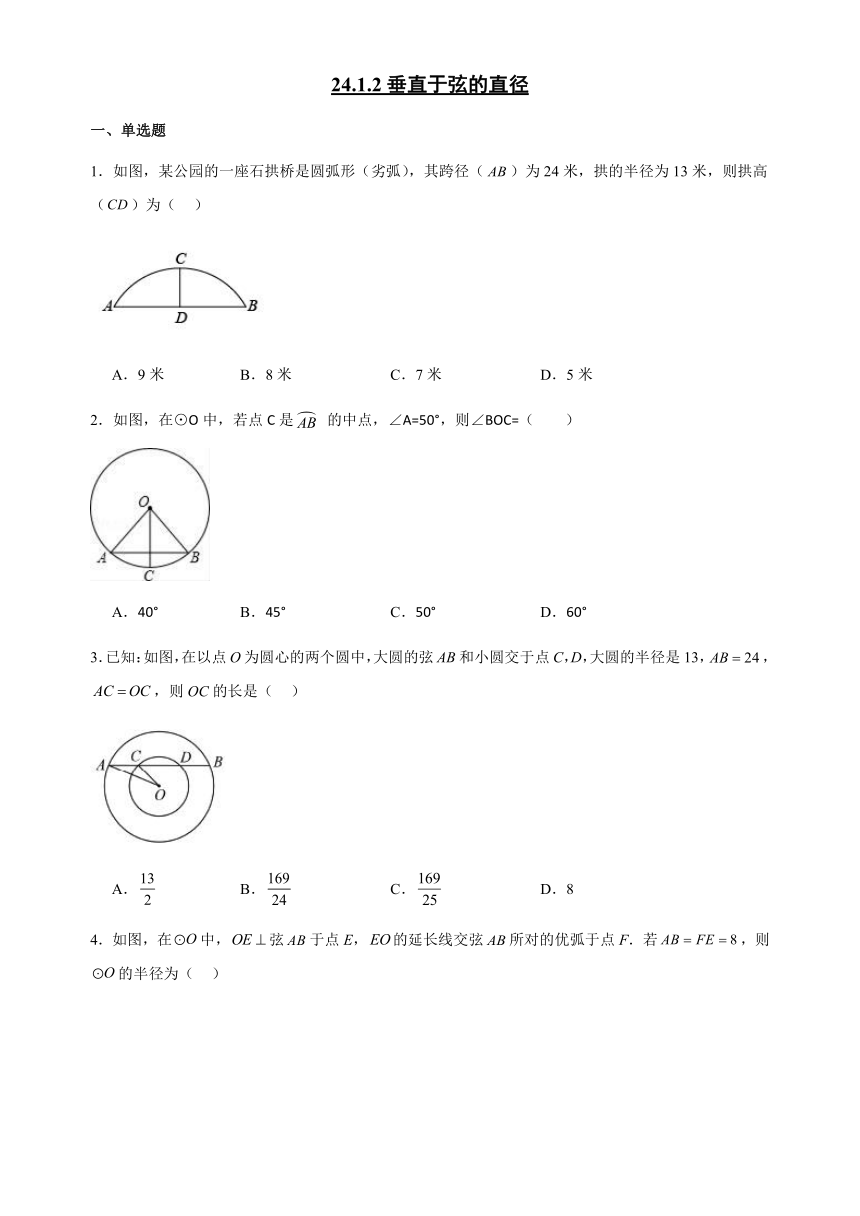
1.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨径()为24米,拱的半径为13米,则拱高()为( )
A.9米 B.8米 C.7米 D.5米
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A. B. C. D.8
4.如图,在中,弦于点E,的延长线交弦所对的优弧于点F.若,则的半径为( )
A.5 B.6 C.4 D.
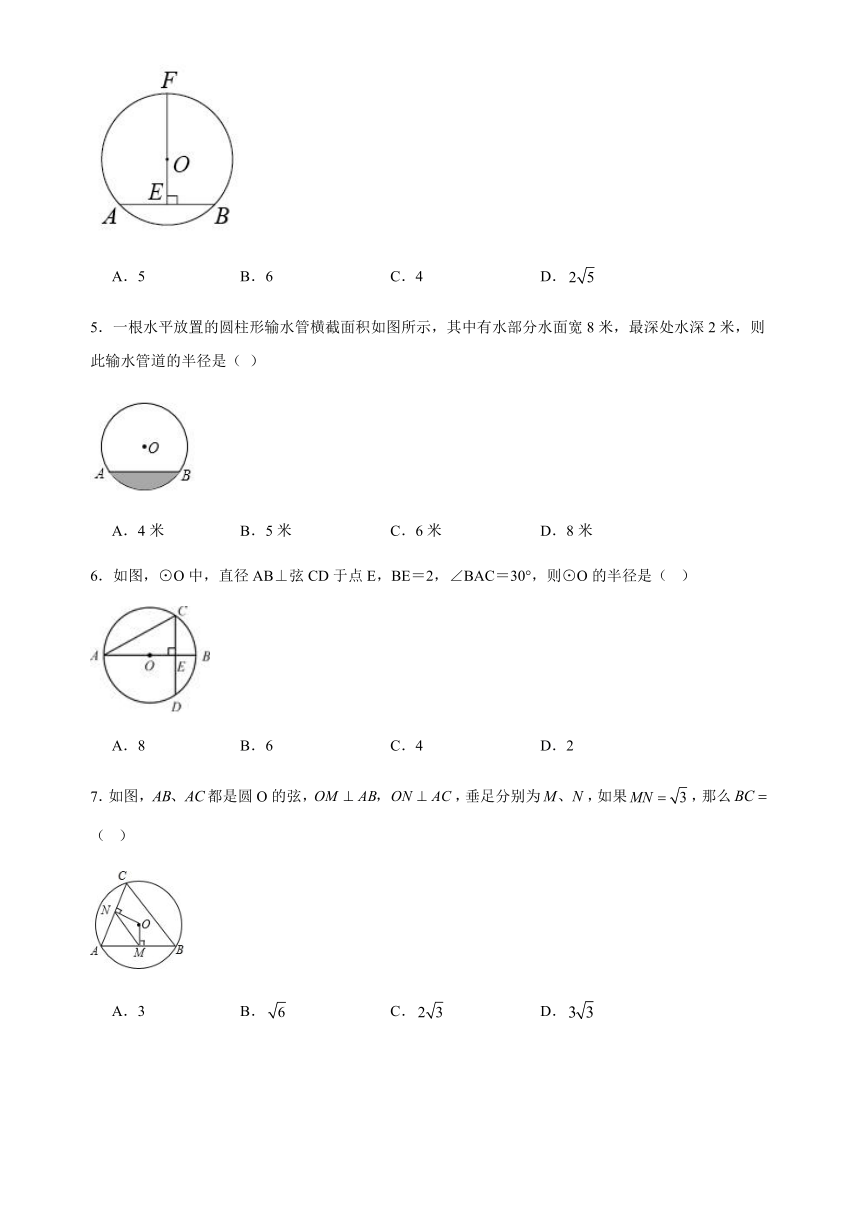
5.一根水平放置的圆柱形输水管横截面积如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.4米 B.5米 C.6米 D.8米
6.如图,⊙O中,直径AB⊥弦CD于点E,BE=2,∠BAC=30°,则⊙O的半径是( )
A.8 B.6 C.4 D.2
7.如图,都是圆O的弦,,垂足分别为,如果,那么( )
A.3 B. C. D.
8.如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是
A.(-4,2) B.(-4.5,2) C.(-5,2) D.(-5.5,2 )
9.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
10.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )
A.(﹣4,5) B.(﹣5,4)
C.(5,﹣4) D.(4,﹣5)
二、填空题
11.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
12.已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,则CD的长为 .
13.如图,是的弦,根据下列条件填空:
(1)如果是的直径,且于点,那么有 , , ;
(2)如果是的直径,且,那么有 , , ;
(3)如果,且,那么有 , , .
14.已知的弦,优弧上的点到的最大距离为1.6,直线,若上有4个不同的点到l的距离等于0.4,则点O到l的距离d的范围为 .
15.一根排水管的截面如图所示,已知排水管的半径,水面宽,如果再注入一些水,当水面AB的宽变为16时,则水面AB上升的高度为 .
16.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
17.将一张半径为4的圆形纸片(如图①)连续对折两次后展开得折痕AB、CD,且AB⊥CD,垂足为M(如图②),之后将纸片如图③翻折,使点B与点M重合,折痕EF与AB相交于点N,连接AE、AF(如图④),则△AEF的面积是 .
三、解答题
18.如图,AB、CD都是⊙O的弦,且AB∥CD,求证:
19.隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)约为,设所在圆的圆心为O,半径,垂足为D.主拱高(弧的中点到弦的距离)约为.连接.求这座石拱桥主桥拱所在圆的半径长.
20.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
21.如图①,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若弧AMD的长为底面周长的,如图②所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
参考答案:
1.B
2.A
3.B
4.A
5.B
6.C
7.C
8.A
9.D
10.A
11.
12.
13. 是的直径
14.
15.2或14/14或2
16.25
17..
18.8
19.
20.8﹣
21.(1)⊙O的半径为8cm;(2)木块的表面积为(384+400)πcm2.
一、单选题
1.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨径()为24米,拱的半径为13米,则拱高()为( )
A.9米 B.8米 C.7米 D.5米
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A. B. C. D.8
4.如图,在中,弦于点E,的延长线交弦所对的优弧于点F.若,则的半径为( )
A.5 B.6 C.4 D.
5.一根水平放置的圆柱形输水管横截面积如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.4米 B.5米 C.6米 D.8米
6.如图,⊙O中,直径AB⊥弦CD于点E,BE=2,∠BAC=30°,则⊙O的半径是( )
A.8 B.6 C.4 D.2
7.如图,都是圆O的弦,,垂足分别为,如果,那么( )
A.3 B. C. D.
8.如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是
A.(-4,2) B.(-4.5,2) C.(-5,2) D.(-5.5,2 )
9.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
10.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )
A.(﹣4,5) B.(﹣5,4)
C.(5,﹣4) D.(4,﹣5)
二、填空题
11.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
12.已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,则CD的长为 .
13.如图,是的弦,根据下列条件填空:
(1)如果是的直径,且于点,那么有 , , ;
(2)如果是的直径,且,那么有 , , ;
(3)如果,且,那么有 , , .
14.已知的弦,优弧上的点到的最大距离为1.6,直线,若上有4个不同的点到l的距离等于0.4,则点O到l的距离d的范围为 .
15.一根排水管的截面如图所示,已知排水管的半径,水面宽,如果再注入一些水,当水面AB的宽变为16时,则水面AB上升的高度为 .
16.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
17.将一张半径为4的圆形纸片(如图①)连续对折两次后展开得折痕AB、CD,且AB⊥CD,垂足为M(如图②),之后将纸片如图③翻折,使点B与点M重合,折痕EF与AB相交于点N,连接AE、AF(如图④),则△AEF的面积是 .
三、解答题
18.如图,AB、CD都是⊙O的弦,且AB∥CD,求证:
19.隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)约为,设所在圆的圆心为O,半径,垂足为D.主拱高(弧的中点到弦的距离)约为.连接.求这座石拱桥主桥拱所在圆的半径长.
20.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
21.如图①,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若弧AMD的长为底面周长的,如图②所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
参考答案:
1.B
2.A
3.B
4.A
5.B
6.C
7.C
8.A
9.D
10.A
11.
12.
13. 是的直径
14.
15.2或14/14或2
16.25
17..
18.8
19.
20.8﹣
21.(1)⊙O的半径为8cm;(2)木块的表面积为(384+400)πcm2.
同课章节目录
