3.5 探索与表达规律 同步练习 (含答案) 2023-2024学年北师大版七年级数学上册
文档属性
| 名称 | 3.5 探索与表达规律 同步练习 (含答案) 2023-2024学年北师大版七年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 21:46:13 | ||
图片预览


文档简介
2023-2024学年北师大版七年级上册
3.5 探索与表达规律 课时同步培优练习
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图所示,由一些点组成形如三角形的图形,每条“边”包括两个顶点有个点,记第个图形中总的点数为,第个图形中总的点数为,依次为,以下说法错误的是( )
A. B.
C. 若,则 D. 若,则
2.我们将如图所示的两种排列形式的点的个数分别称作“三角形数”如,,,和“正方形数”如,,,,在小于的数中,设最大的“三角形数”为,最大的“正方形数”为,则的值为( )
A. B. C. D.
3.观察下列图形:
它们是按一定规律排列的,依照此规律,第 为正整数个图形中共有的点数是( )
A. B. C. D.
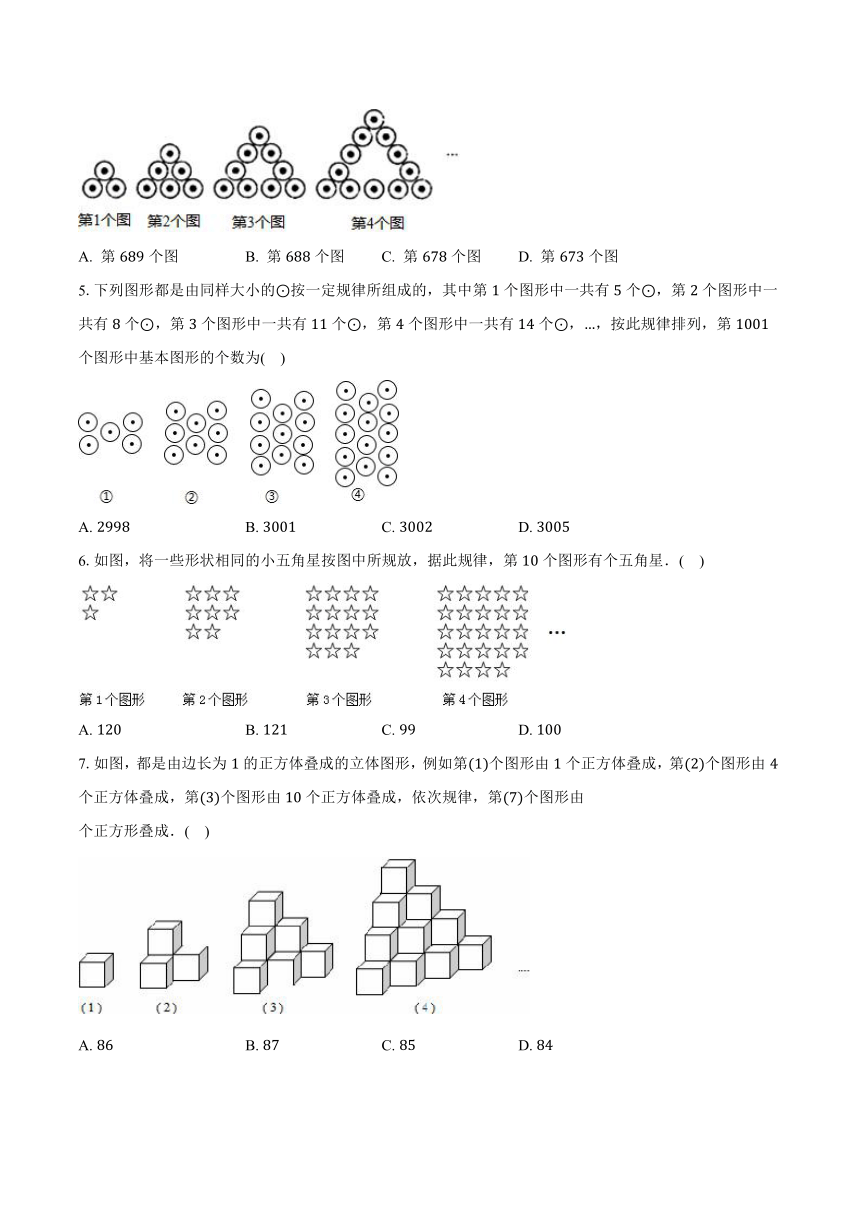
4.如图,图中“”是按一定的规律排列,根据此规律,有个“”图案的是( )
A. 第个图 B. 第个图 C. 第个图 D. 第个图
5.下列图形都是由同样大小的按一定规律所组成的,其中第个图形中一共有个,第个图形中一共有个,第个图形中一共有个,第个图形中一共有个,,按此规律排列,第个图形中基本图形的个数为( )
A. B. C. D.
6.如图,将一些形状相同的小五角星按图中所规放,据此规律,第个图形有个五角星.( )
A. B. C. D.
7.如图,都是由边长为的正方体叠成的立体图形,例如第个图形由个正方体叠成,第个图形由个正方体叠成,第个图形由个正方体叠成,依次规律,第个图形由
个正方形叠成.( )
A. B. C. D.
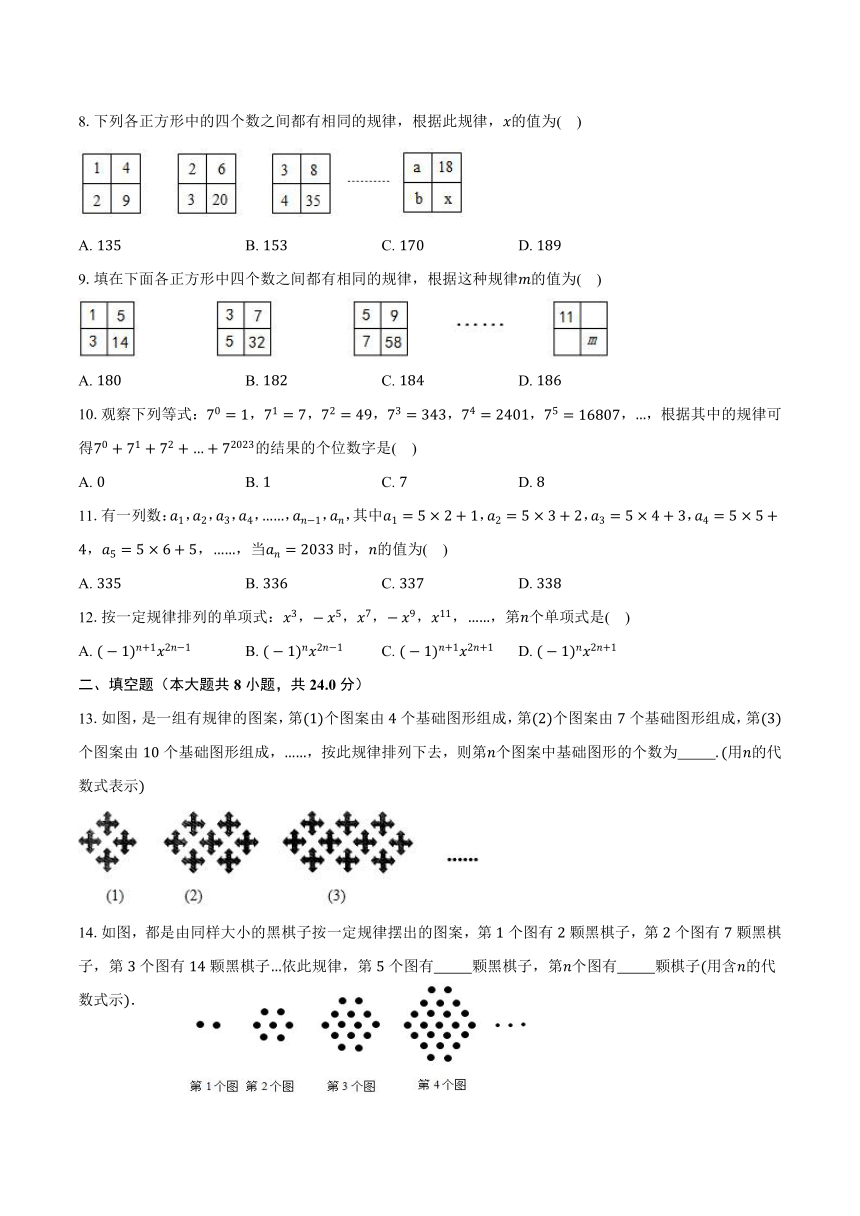
8.下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A. B. C. D.
9.填在下面各正方形中四个数之间都有相同的规律,根据这种规律的值为( )
A. B. C. D.
10.观察下列等式:,,,,,,,根据其中的规律可得的结果的个位数字是( )
A. B. C. D.
11.有一列数:,,,,,,,其中,,,,,,当时,的值为( )
A. B. C. D.
12.按一定规律排列的单项式:,,,,,,第个单项式是( )
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
13.如图,是一组有规律的图案,第个图案由个基础图形组成,第个图案由个基础图形组成,第个图案由个基础图形组成,,按此规律排列下去,则第个图案中基础图形的个数为 用的代数式表示
14.如图,都是由同样大小的黑棋子按一定规律摆出的图案,第个图有颗黑棋子,第个图有颗黑棋子,第个图有颗黑棋子依此规律,第个图有 颗黑棋子,第个图有 颗棋子用含的代数式示.
15.如图是用火柴棒拼成的一组图形,第个图形有根火柴棒,第个图形有根火柴棒第个图形有根火柴棒,第个图形有根火柴棒,按此规律拼下去,则第个图形需______火柴棒.
16.观察下列图形,它们是按一定规律排列的,第个图形由颗五角星组成,第个图形由颗五角星组成,,第个图形由______ 颗五角星组成.
17.如表在我国宋朝数学家杨辉年的著作详解九章算法中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全表第四行空缺的数字是______ .
18.有一组单项式依次为,,,,,,则第个单项式为______.
19.如图,将一个边长为的正方形纸片分割成个部分,部分是边长为的正方形纸片面积的一半,部分是部分面积的一半,部分是部分面积的一半,依此类推,求出的值______.
20.观察下面的变化规律:
,,,,
根据上面的规律计算: .
三、解答题(本大题共5小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
21.本小题分 如图,自行车每节链条的长度为,交叉重叠部分的圆的直径为.
节链条长_________;
节链条长__________;
如果一辆型自行车的链条由节这样的链条组成,那么这辆自行车上链条总长度是多少?
22.本小题分 下列是用火柴棒拼出的一列图形:
仔细观察,找出规律,解答下列各题:
第个图形中共有______根火柴,第个图形中共有______根火柴;
第个形中共有______根火柴用含的式子表示;
若,如,规定,,如:,求的值请给出你的计算过程。
23.本小题分 将一个面积为的等腰直角三角形进行次划分后得到三个等腰直角三角形,再进行第次划分可得到五个等腰直角三角形,依次进行下去.
完成下面表格:
划分的次数 ______
等腰直角三角形总个数 ______ ______
观察图形,完成下面表格:
第次划分后
阴影部分面积 ______
阴影部分面积还可以表示为 ______
根据表格所呈现的规律,可得______结果用幂的形式表示.
请利用如图面积的分割,直接写出______.
24.本小题分 观察与思考:我们知道,那么结果等于多少呢?
请你仔细观察,找出下面图形与算式的关系,解决下列问题:
尝试:第个图形可以表示的等式是___________________;
概括:___________________;
拓展应用:求的值.
25.本小题分 芳芳妈妈买了一块正方形地毯,地毯上有“”组成的图案,观察局部有以下规律:芳芳数的个数的方法是用“”来划分,从右上角的个开始,一层一层往外数,第一层个,第二层个,第三层个,这样她发现了连续奇数求和的方法.
通过阅读以上材料,请完成下列问题:
_________.
_________.
_________.
到之间,所有能被整除的奇数的和为_________.
3.5 探索与表达规律课时同步培优练习答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:;
;
因为自行车上的链条为环形,在展直的基础上还要缩短,
故这辆自行车链条的总长为厘米,
故答案为.
22. 解:;;
;
。
23. 解:当划分次时,等腰直角三角形的个数为,
则划分次时,等腰直角三角形的个数为:,
故当在等腰三角形个时,,解得:,
第次划分时,阴影部分的面积为:,还可以表示为:,
故,
.
24. 解:;
;
.
25. 解:根据阅读材料中计算结果的规律可得:
.
根据阅读材料中计算结果的规律可得:
.
故答案为;
.
由题意得,所有奇数的和
.
3.5 探索与表达规律 课时同步培优练习
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图所示,由一些点组成形如三角形的图形,每条“边”包括两个顶点有个点,记第个图形中总的点数为,第个图形中总的点数为,依次为,以下说法错误的是( )
A. B.
C. 若,则 D. 若,则
2.我们将如图所示的两种排列形式的点的个数分别称作“三角形数”如,,,和“正方形数”如,,,,在小于的数中,设最大的“三角形数”为,最大的“正方形数”为,则的值为( )
A. B. C. D.
3.观察下列图形:
它们是按一定规律排列的,依照此规律,第 为正整数个图形中共有的点数是( )
A. B. C. D.
4.如图,图中“”是按一定的规律排列,根据此规律,有个“”图案的是( )
A. 第个图 B. 第个图 C. 第个图 D. 第个图
5.下列图形都是由同样大小的按一定规律所组成的,其中第个图形中一共有个,第个图形中一共有个,第个图形中一共有个,第个图形中一共有个,,按此规律排列,第个图形中基本图形的个数为( )
A. B. C. D.
6.如图,将一些形状相同的小五角星按图中所规放,据此规律,第个图形有个五角星.( )
A. B. C. D.
7.如图,都是由边长为的正方体叠成的立体图形,例如第个图形由个正方体叠成,第个图形由个正方体叠成,第个图形由个正方体叠成,依次规律,第个图形由
个正方形叠成.( )
A. B. C. D.
8.下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A. B. C. D.
9.填在下面各正方形中四个数之间都有相同的规律,根据这种规律的值为( )
A. B. C. D.
10.观察下列等式:,,,,,,,根据其中的规律可得的结果的个位数字是( )
A. B. C. D.
11.有一列数:,,,,,,,其中,,,,,,当时,的值为( )
A. B. C. D.
12.按一定规律排列的单项式:,,,,,,第个单项式是( )
A. B. C. D.
二、填空题(本大题共8小题,共24.0分)
13.如图,是一组有规律的图案,第个图案由个基础图形组成,第个图案由个基础图形组成,第个图案由个基础图形组成,,按此规律排列下去,则第个图案中基础图形的个数为 用的代数式表示
14.如图,都是由同样大小的黑棋子按一定规律摆出的图案,第个图有颗黑棋子,第个图有颗黑棋子,第个图有颗黑棋子依此规律,第个图有 颗黑棋子,第个图有 颗棋子用含的代数式示.
15.如图是用火柴棒拼成的一组图形,第个图形有根火柴棒,第个图形有根火柴棒第个图形有根火柴棒,第个图形有根火柴棒,按此规律拼下去,则第个图形需______火柴棒.
16.观察下列图形,它们是按一定规律排列的,第个图形由颗五角星组成,第个图形由颗五角星组成,,第个图形由______ 颗五角星组成.
17.如表在我国宋朝数学家杨辉年的著作详解九章算法中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全表第四行空缺的数字是______ .
18.有一组单项式依次为,,,,,,则第个单项式为______.
19.如图,将一个边长为的正方形纸片分割成个部分,部分是边长为的正方形纸片面积的一半,部分是部分面积的一半,部分是部分面积的一半,依此类推,求出的值______.
20.观察下面的变化规律:
,,,,
根据上面的规律计算: .
三、解答题(本大题共5小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
21.本小题分 如图,自行车每节链条的长度为,交叉重叠部分的圆的直径为.
节链条长_________;
节链条长__________;
如果一辆型自行车的链条由节这样的链条组成,那么这辆自行车上链条总长度是多少?
22.本小题分 下列是用火柴棒拼出的一列图形:
仔细观察,找出规律,解答下列各题:
第个图形中共有______根火柴,第个图形中共有______根火柴;
第个形中共有______根火柴用含的式子表示;
若,如,规定,,如:,求的值请给出你的计算过程。
23.本小题分 将一个面积为的等腰直角三角形进行次划分后得到三个等腰直角三角形,再进行第次划分可得到五个等腰直角三角形,依次进行下去.
完成下面表格:
划分的次数 ______
等腰直角三角形总个数 ______ ______
观察图形,完成下面表格:
第次划分后
阴影部分面积 ______
阴影部分面积还可以表示为 ______
根据表格所呈现的规律,可得______结果用幂的形式表示.
请利用如图面积的分割,直接写出______.
24.本小题分 观察与思考:我们知道,那么结果等于多少呢?
请你仔细观察,找出下面图形与算式的关系,解决下列问题:
尝试:第个图形可以表示的等式是___________________;
概括:___________________;
拓展应用:求的值.
25.本小题分 芳芳妈妈买了一块正方形地毯,地毯上有“”组成的图案,观察局部有以下规律:芳芳数的个数的方法是用“”来划分,从右上角的个开始,一层一层往外数,第一层个,第二层个,第三层个,这样她发现了连续奇数求和的方法.
通过阅读以上材料,请完成下列问题:
_________.
_________.
_________.
到之间,所有能被整除的奇数的和为_________.
3.5 探索与表达规律课时同步培优练习答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:;
;
因为自行车上的链条为环形,在展直的基础上还要缩短,
故这辆自行车链条的总长为厘米,
故答案为.
22. 解:;;
;
。
23. 解:当划分次时,等腰直角三角形的个数为,
则划分次时,等腰直角三角形的个数为:,
故当在等腰三角形个时,,解得:,
第次划分时,阴影部分的面积为:,还可以表示为:,
故,
.
24. 解:;
;
.
25. 解:根据阅读材料中计算结果的规律可得:
.
根据阅读材料中计算结果的规律可得:
.
故答案为;
.
由题意得,所有奇数的和
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
