第12章《一次函数》章末检测题 (含答案) 2023-2024学年八年级上册数学沪科版
文档属性
| 名称 | 第12章《一次函数》章末检测题 (含答案) 2023-2024学年八年级上册数学沪科版 |  | |
| 格式 | docx | ||
| 文件大小 | 299.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 21:57:28 | ||
图片预览

文档简介
第12章《一次函数》章末检测题
2023-2024学年八年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.函数y=中,自变量的取值范围是( )
A.x≥0 B.x≠1 C.x>1 D.x≥0,且x≠1
2.如图所示,一次函数的图像经过A、B两点,则解集是( )
A. B. C. D.
3.下列函数中,是一次函数的是( )
A. B. C. D.
4.把函数y=3x﹣3的图象沿x轴正方向水平向右平移2个单位后的解析式是( )
A.y=3x﹣9 B.y=3x﹣6 C.y=3x﹣5 D.y=3x﹣1
5.一次函数与的图像如下图所示,则的解集为( )
A. B. C. D.
6.函数的图象如图所示.则关于x的不等式的解集为( )
A. B. C. D.
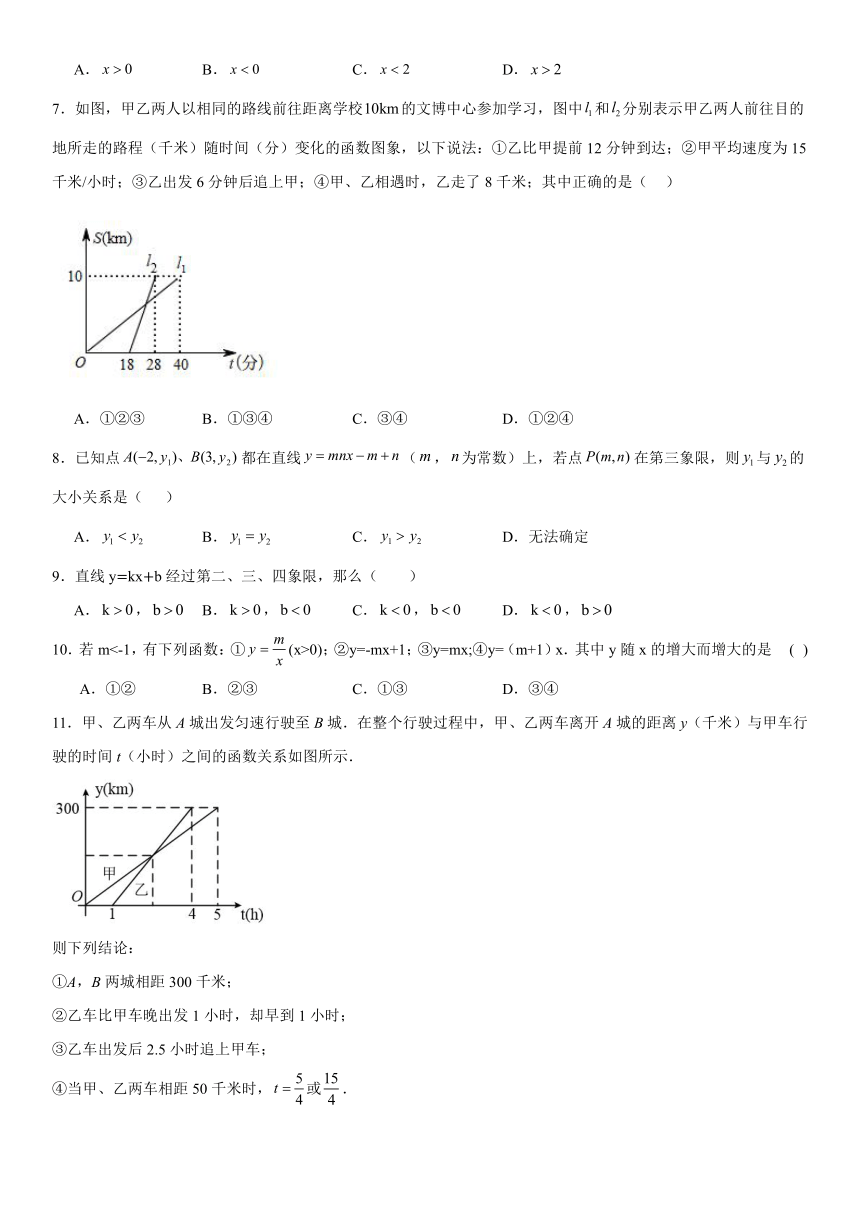
7.如图,甲乙两人以相同的路线前往距离学校的文博中心参加学习,图中和分别表示甲乙两人前往目的地所走的路程(千米)随时间(分)变化的函数图象,以下说法:①乙比甲提前12分钟到达;②甲平均速度为15千米/小时;③乙出发6分钟后追上甲;④甲、乙相遇时,乙走了8千米;其中正确的是( )
A.①②③ B.①③④ C.③④ D.①②④
8.已知点都在直线(,为常数)上,若点在第三象限,则与的大小关系是( )
A. B. C. D.无法确定
9.直线y=kx+b经过第二、三、四象限,那么( )
A., B., C., D.,
10.若m<-1,有下列函数:①(x>0);②y=-mx+1;③y=mx;④y=(m+1)x.其中y随x的增大而增大的是 ( )
A.①② B.②③ C.①③ D.③④
11.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)
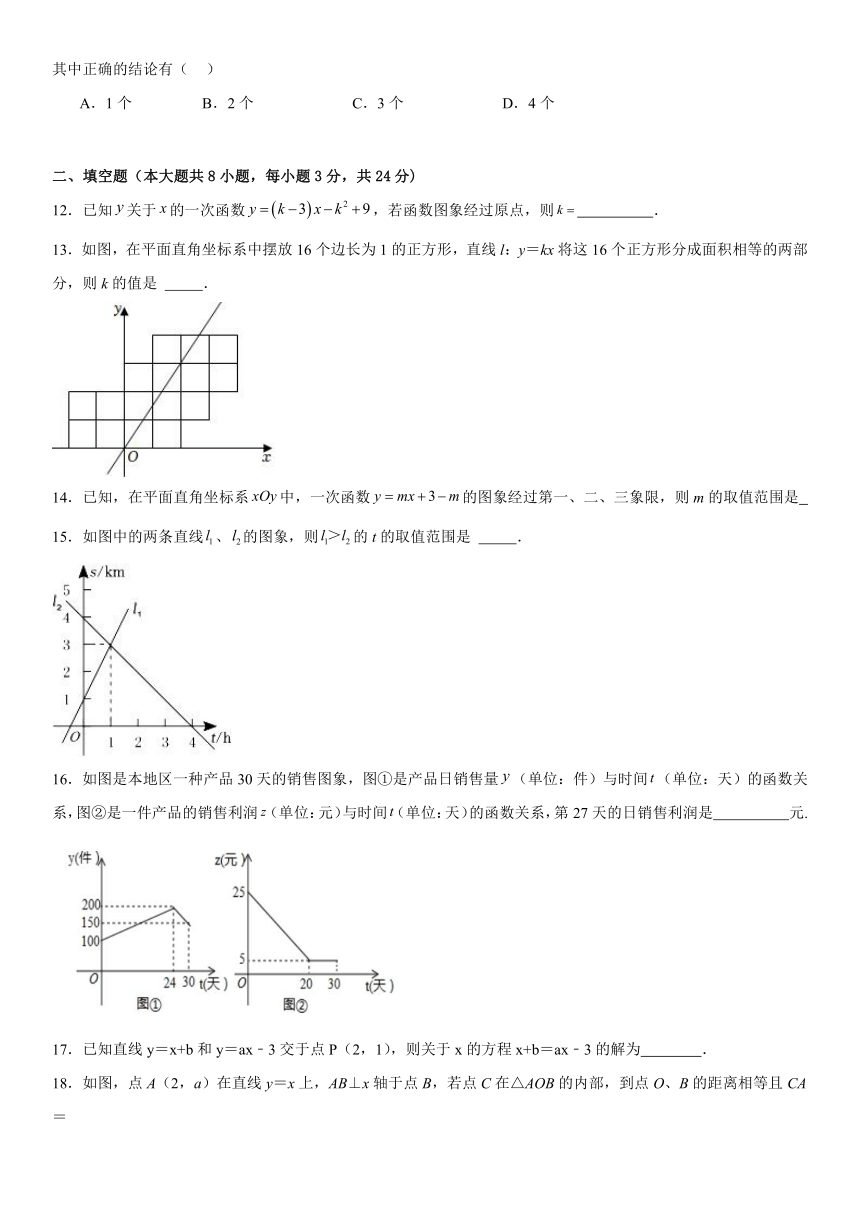
12.已知关于的一次函数,若函数图象经过原点,则 .
13.如图,在平面直角坐标系中摆放16个边长为1的正方形,直线l:y=kx将这16个正方形分成面积相等的两部分,则k的值是 .
14.已知,在平面直角坐标系中,一次函数的图象经过第一、二、三象限,则m的取值范围是
15.如图中的两条直线、的图象,则的t的取值范围是 .
16.如图是本地区一种产品30天的销售图象,图①是产品日销售量(单位:件)与时间(单位:天)的函数关系,图②是一件产品的销售利润(单位:元)与时间(单位:天)的函数关系,第27天的日销售利润是 元.
17.已知直线y=x+b和y=ax﹣3交于点P(2,1),则关于x的方程x+b=ax﹣3的解为 .
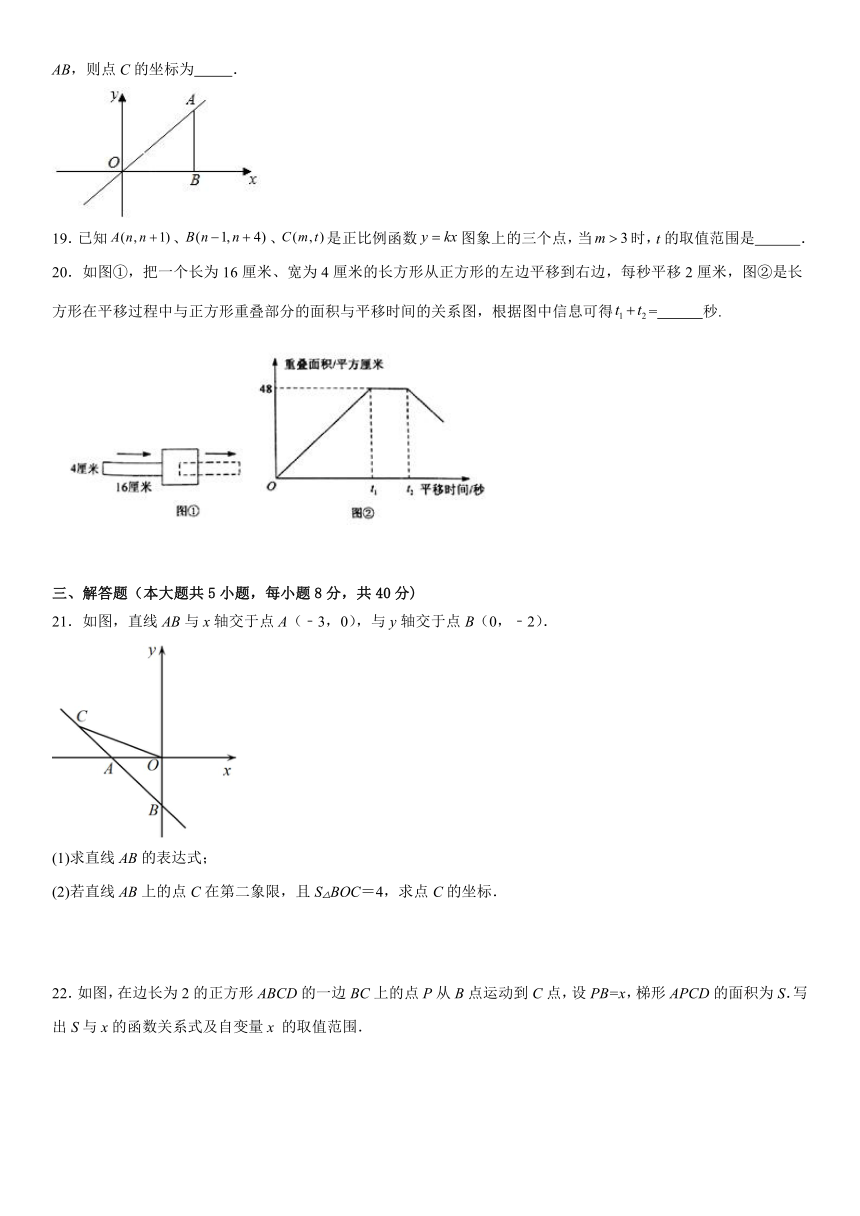
18.如图,点A(2,a)在直线y=x上,AB⊥x轴于点B,若点C在△AOB的内部,到点O、B的距离相等且CA=
AB,则点C的坐标为 .
19.已知、、是正比例函数图象上的三个点,当时,t的取值范围是 .
20.如图①,把一个长为16厘米、宽为4厘米的长方形从正方形的左边平移到右边,每秒平移2厘米,图②是长方形在平移过程中与正方形重叠部分的面积与平移时间的关系图,根据图中信息可得= 秒.
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,直线AB与x轴交于点A(﹣3,0),与y轴交于点B(0,﹣2).
(1)求直线AB的表达式;
(2)若直线AB上的点C在第二象限,且S△BOC=4,求点C的坐标.
22.如图,在边长为2的正方形ABCD的一边BC上的点P从B点运动到C点,设PB=x,梯形APCD的面积为S.写出S与x的函数关系式及自变量x 的取值范围.
23.已知如图:直线和直线相交于,B、C分别为两条直线与y轴的交点.
(1)求a、b的值;
(2)求的面积.
24. 已知:如图,在平面直角坐标系中,一次函数的图象分别与轴交于点A、 B,点在轴上,若,求直线PB的函数解析式.
25.小李计划从网上批发一些饰品摆摊售卖.经过多方调查,仔细甄别,他选定了A、B两款网红饰品,其进价分别为每个x元、y元.已知购进A款饰品8个和B款饰品6个所需花费相同;购进A款饰品10个和B
款饰品4个共需230元.
(1)请求出A,B两款饰品的进价分别是多少?
(2)小李计划购进两款饰品共计100个(其中A款饰品最多62个),要使所需费用不多于1700元,则他有哪几种购进方案?哪种方案的费用最低?最低费用为多少?
参考答案:
1.D
2.B
3.D
4.A
5.A
6.D
7.A
8.A
9.C
10.A
11.B
12.
13.
14.
15.t>1/
16.875
17.x=2
18.(1,2﹣).
19.
20.14.
21.(1)
(2)( 4,)
22.(0<x<2)
23.(1),
(2)
24.直线的函数解析式为或.
25.(1)A款饰品的进价是15元,B款饰品的进价是20元
(2)购进62个A款饰品,38个B款饰品费用最低,最低费用为1690元
2023-2024学年八年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.函数y=中,自变量的取值范围是( )
A.x≥0 B.x≠1 C.x>1 D.x≥0,且x≠1
2.如图所示,一次函数的图像经过A、B两点,则解集是( )
A. B. C. D.
3.下列函数中,是一次函数的是( )
A. B. C. D.
4.把函数y=3x﹣3的图象沿x轴正方向水平向右平移2个单位后的解析式是( )
A.y=3x﹣9 B.y=3x﹣6 C.y=3x﹣5 D.y=3x﹣1
5.一次函数与的图像如下图所示,则的解集为( )
A. B. C. D.
6.函数的图象如图所示.则关于x的不等式的解集为( )
A. B. C. D.
7.如图,甲乙两人以相同的路线前往距离学校的文博中心参加学习,图中和分别表示甲乙两人前往目的地所走的路程(千米)随时间(分)变化的函数图象,以下说法:①乙比甲提前12分钟到达;②甲平均速度为15千米/小时;③乙出发6分钟后追上甲;④甲、乙相遇时,乙走了8千米;其中正确的是( )
A.①②③ B.①③④ C.③④ D.①②④
8.已知点都在直线(,为常数)上,若点在第三象限,则与的大小关系是( )
A. B. C. D.无法确定
9.直线y=kx+b经过第二、三、四象限,那么( )
A., B., C., D.,
10.若m<-1,有下列函数:①(x>0);②y=-mx+1;③y=mx;④y=(m+1)x.其中y随x的增大而增大的是 ( )
A.①② B.②③ C.①③ D.③④
11.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,或.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)
12.已知关于的一次函数,若函数图象经过原点,则 .
13.如图,在平面直角坐标系中摆放16个边长为1的正方形,直线l:y=kx将这16个正方形分成面积相等的两部分,则k的值是 .
14.已知,在平面直角坐标系中,一次函数的图象经过第一、二、三象限,则m的取值范围是
15.如图中的两条直线、的图象,则的t的取值范围是 .
16.如图是本地区一种产品30天的销售图象,图①是产品日销售量(单位:件)与时间(单位:天)的函数关系,图②是一件产品的销售利润(单位:元)与时间(单位:天)的函数关系,第27天的日销售利润是 元.
17.已知直线y=x+b和y=ax﹣3交于点P(2,1),则关于x的方程x+b=ax﹣3的解为 .
18.如图,点A(2,a)在直线y=x上,AB⊥x轴于点B,若点C在△AOB的内部,到点O、B的距离相等且CA=
AB,则点C的坐标为 .
19.已知、、是正比例函数图象上的三个点,当时,t的取值范围是 .
20.如图①,把一个长为16厘米、宽为4厘米的长方形从正方形的左边平移到右边,每秒平移2厘米,图②是长方形在平移过程中与正方形重叠部分的面积与平移时间的关系图,根据图中信息可得= 秒.
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,直线AB与x轴交于点A(﹣3,0),与y轴交于点B(0,﹣2).
(1)求直线AB的表达式;
(2)若直线AB上的点C在第二象限,且S△BOC=4,求点C的坐标.
22.如图,在边长为2的正方形ABCD的一边BC上的点P从B点运动到C点,设PB=x,梯形APCD的面积为S.写出S与x的函数关系式及自变量x 的取值范围.
23.已知如图:直线和直线相交于,B、C分别为两条直线与y轴的交点.
(1)求a、b的值;
(2)求的面积.
24. 已知:如图,在平面直角坐标系中,一次函数的图象分别与轴交于点A、 B,点在轴上,若,求直线PB的函数解析式.
25.小李计划从网上批发一些饰品摆摊售卖.经过多方调查,仔细甄别,他选定了A、B两款网红饰品,其进价分别为每个x元、y元.已知购进A款饰品8个和B款饰品6个所需花费相同;购进A款饰品10个和B
款饰品4个共需230元.
(1)请求出A,B两款饰品的进价分别是多少?
(2)小李计划购进两款饰品共计100个(其中A款饰品最多62个),要使所需费用不多于1700元,则他有哪几种购进方案?哪种方案的费用最低?最低费用为多少?
参考答案:
1.D
2.B
3.D
4.A
5.A
6.D
7.A
8.A
9.C
10.A
11.B
12.
13.
14.
15.t>1/
16.875
17.x=2
18.(1,2﹣).
19.
20.14.
21.(1)
(2)( 4,)
22.(0<x<2)
23.(1),
(2)
24.直线的函数解析式为或.
25.(1)A款饰品的进价是15元,B款饰品的进价是20元
(2)购进62个A款饰品,38个B款饰品费用最低,最低费用为1690元
