人教版七年级下册数学《9.3 一元一次不等式组》 课时练
文档属性
| 名称 | 人教版七年级下册数学《9.3 一元一次不等式组》 课时练 |  | |
| 格式 | docx | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 13:06:11 | ||
图片预览


文档简介
人教版七年级下册数学
《9.3 一元一次不等式组》课时练
一、单选题
1.不等式组的整数解的个数是( ).
A.0个 B.2个 C.4个 D.5个
2.个关于的一元一次不等式组的解集在数轴上的表示如图所示,则该不等式组的解集是( )
A. B. C. D.
3.若不等式组的整数解共有三个,则a的取值范围是( )
A.4<a<5 B.4≤a<5 C.4<a≤5 D.4≤a≤5
4.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
5.不等式组 的正整数解有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在数轴上A,B,C,D四个点所对应的数中是不等式组的解的是( )
A.点A对应的数 B.点B对应的数
C.点C对应的数 D.点D对应的数
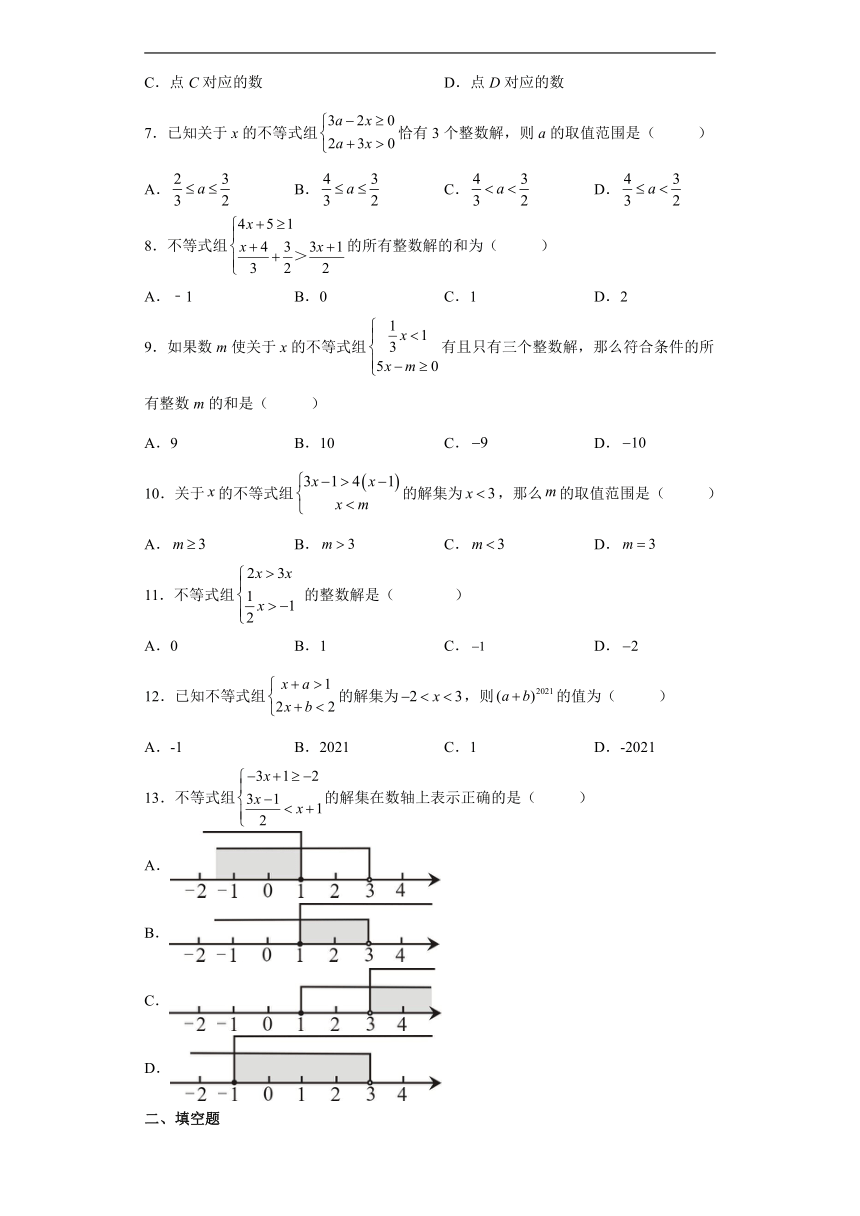
7.已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
8.不等式组的所有整数解的和为( )
A.﹣1 B.0 C.1 D.2
9.如果数m使关于x的不等式组有且只有三个整数解,那么符合条件的所有整数m的和是( )
A.9 B.10 C. D.
10.关于的不等式组的解集为,那么的取值范围是( )
A. B. C. D.
11.不等式组 的整数解是( )
A.0 B.1 C. D.
12.已知不等式组的解集为,则的值为( )
A.-1 B.2021 C.1 D.-2021
13.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
二、填空题
14.不等式组的解集是___________.
15.若不等式组无解,则a的取值范围是________.
16.若关于x的不等式组有2整数解,则m的取值范围是_______
17.冬季运动越野滑雪的路段分为上坡、平地、下坡三种类型,滑雪者在同种路段中滑行速度保持不变.运动爱好者小明上坡滑雪3分钟与平地滑雪2分钟的路程相等.第一次训练中,他上坡、平地、下坡滑雪的时间分别是2分钟、2分钟、3分钟.第二次训练中,他上坡、平地、下坡滑雪的时间分别比第一次多了50%、50%、20%,总路程比第一次多32%.第三次训练所用时间为第一次的3倍,其中上坡、平地、下坡滑雪的时间依次减少,且总路程是第二次的2倍.设第三次训练中平地滑雪时间为b分钟,若b为整数,则b的值为 _____.
18.如图,用图1中的a张长方形和b张正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒,若a+b的值在285和315之间(不含285与315),且用完这些纸板做竖式纸盒比横式纸盒多30个,则a的值可能是____________.
三、解答题
19.解不等式组:,并写出它的所有整数解.
20.解不等式组请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
21.解不等式
(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组
22.九(1)班同学在社会实践调研活动中发现,某服装店销售A,B两种款式的衬衫,进价和售价如表所示:
项目 进价(元/件) 售价(元/件)
A 100 120
B 150 200
已知该服装店购进A,B两种款式的衬衫共花费6000元,销售完成后共获得利润1600元.
(1)服装店购进A,B两种款式的衬衫各多少件?
(2)若服装店再次购进A,B两种款式的衬衫共30件,其中B款式的数量不多于A款式数量的2倍,且两种衬衫总利润不低于1140元.问共有几种购进方案?请写出利润最大的购进方案.
23.小李计划从网上批发一些饰品摆摊售卖.经过多方调查,仔细甄别,他选定了A、B两款网红饰品,其进价分别为每个x元、y元.已知购进A款饰品8个和B款饰品6 个所需花费相同;购进A款饰品 10个和B款饰品4个共需230元.
(1)请求出 A,B两款饰品的进价分别是多少
(2)小李计划购进两款饰品共计100个(其中A款饰品最多62个),要使所需费用不多于 1700元,则他有哪几种购进方案
(3)小李最后准备将A、B两款饰品单价分别定为21元、28元.他计划按照(2)中能够获得最大利润的方案购进,而且为吸引顾客,他准备在售卖过程中,给予顾客不同金额的现金红包,若要保证最后的利润率不低于 35%,那么他给出的红包总额不能超过多少元?
参考答案
1.C
2.D
3.C
4.A
5.C
6.B
7.B
8.B
9.D
10.A
11.C
12.A
13.A
14.
15.
16.417.7
18.218,225,232
19.,整数解是
解:
由①解得:
由②解得:
所以不等式组的解集为
其中是整数的解为0,1.
20.(1)移项得:x≥2 1
即x≥1
故答案为:x≥1
(2)移项得:
合并同类项得:
系数化为1得:x≤2
故答案为:x≤2
(3)把不等式①和②的解集在数轴上表示出来如下图所示:
(4)由上图知,原不等式组的解集为:﹣1 ≤ x≤2
故答案为:﹣1 ≤ x≤2
21.(1)解:
去分母得:,
去括号得:,
移项合并得:,
∴不等式的解集为,
在数轴上表示为:
(2)解:,
解不等式得,,
解不等式得,,
∴不等式组的解集为.
22.(1)解:设服装店购进种款式的衬衫件,购进种款式的衬衫件,
由题意得:,
解得,
答:服装店购进种款式的衬衫30件,购进种款式的衬衫20件.
(2)解:设服装店购进种款式的衬衫件,则购进种款式的衬衫件,
由题意得:,
解得,
因为为正整数,
所以的所有可能取值为,
当时,总利润为(元),
当时,总利润为(元),
当时,总利润为(元),
答:共有3种购进方案,利润最大的购进方案是购进种款式的衬衫10件,购进种款式的衬衫20件.
23.(1)解:设A款饰品的进价是x元,B款饰品的进价是y元,根据题意,得
,解得:,
答:A,B两款饰品的进价分别是15元,20元;
(2)解:设购进A款饰品m个,则购进B款饰品(100-m)个,根据题意,得
,解得:60≤m≤62,
当m=60时,100-m=40,
当m=61时,100-m=39,
当m=62时,100-m=38,
∴共有3种方案,
方案一:设购进A款饰品60个,购进B款饰品40个;
方案二:设购进A款饰品61个,购进B款饰品39个;
方案三:设购进A款饰品62个,购进B款饰品38个;
答:他有哪3种购进方案,方案一:设购进A款饰品60个,购进B款饰品40个;方案二:设购进A款饰品61个,购进B款饰品39个;方案三:设购进A款饰品62个,购进B款饰品38个;
(3)解:∵按方案一,获得利润为:60(21-15)+40(27-20)=640(元),
按方案二,获得利润为:61(21-15)+39(27-20)=639(元),
按方案三,获得利润为:62(21-15)+38(27-20)=638(元),
∴他是按按方案一进货,
设他给出的红包总额为p元,根据题意,得
,
解得:p≤45,
答:他给出的红包总额不能超过45元.
《9.3 一元一次不等式组》课时练
一、单选题
1.不等式组的整数解的个数是( ).
A.0个 B.2个 C.4个 D.5个
2.个关于的一元一次不等式组的解集在数轴上的表示如图所示,则该不等式组的解集是( )
A. B. C. D.
3.若不等式组的整数解共有三个,则a的取值范围是( )
A.4<a<5 B.4≤a<5 C.4<a≤5 D.4≤a≤5
4.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
5.不等式组 的正整数解有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在数轴上A,B,C,D四个点所对应的数中是不等式组的解的是( )
A.点A对应的数 B.点B对应的数
C.点C对应的数 D.点D对应的数
7.已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
8.不等式组的所有整数解的和为( )
A.﹣1 B.0 C.1 D.2
9.如果数m使关于x的不等式组有且只有三个整数解,那么符合条件的所有整数m的和是( )
A.9 B.10 C. D.
10.关于的不等式组的解集为,那么的取值范围是( )
A. B. C. D.
11.不等式组 的整数解是( )
A.0 B.1 C. D.
12.已知不等式组的解集为,则的值为( )
A.-1 B.2021 C.1 D.-2021
13.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
二、填空题
14.不等式组的解集是___________.
15.若不等式组无解,则a的取值范围是________.
16.若关于x的不等式组有2整数解,则m的取值范围是_______
17.冬季运动越野滑雪的路段分为上坡、平地、下坡三种类型,滑雪者在同种路段中滑行速度保持不变.运动爱好者小明上坡滑雪3分钟与平地滑雪2分钟的路程相等.第一次训练中,他上坡、平地、下坡滑雪的时间分别是2分钟、2分钟、3分钟.第二次训练中,他上坡、平地、下坡滑雪的时间分别比第一次多了50%、50%、20%,总路程比第一次多32%.第三次训练所用时间为第一次的3倍,其中上坡、平地、下坡滑雪的时间依次减少,且总路程是第二次的2倍.设第三次训练中平地滑雪时间为b分钟,若b为整数,则b的值为 _____.
18.如图,用图1中的a张长方形和b张正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒,若a+b的值在285和315之间(不含285与315),且用完这些纸板做竖式纸盒比横式纸盒多30个,则a的值可能是____________.
三、解答题
19.解不等式组:,并写出它的所有整数解.
20.解不等式组请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
21.解不等式
(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组
22.九(1)班同学在社会实践调研活动中发现,某服装店销售A,B两种款式的衬衫,进价和售价如表所示:
项目 进价(元/件) 售价(元/件)
A 100 120
B 150 200
已知该服装店购进A,B两种款式的衬衫共花费6000元,销售完成后共获得利润1600元.
(1)服装店购进A,B两种款式的衬衫各多少件?
(2)若服装店再次购进A,B两种款式的衬衫共30件,其中B款式的数量不多于A款式数量的2倍,且两种衬衫总利润不低于1140元.问共有几种购进方案?请写出利润最大的购进方案.
23.小李计划从网上批发一些饰品摆摊售卖.经过多方调查,仔细甄别,他选定了A、B两款网红饰品,其进价分别为每个x元、y元.已知购进A款饰品8个和B款饰品6 个所需花费相同;购进A款饰品 10个和B款饰品4个共需230元.
(1)请求出 A,B两款饰品的进价分别是多少
(2)小李计划购进两款饰品共计100个(其中A款饰品最多62个),要使所需费用不多于 1700元,则他有哪几种购进方案
(3)小李最后准备将A、B两款饰品单价分别定为21元、28元.他计划按照(2)中能够获得最大利润的方案购进,而且为吸引顾客,他准备在售卖过程中,给予顾客不同金额的现金红包,若要保证最后的利润率不低于 35%,那么他给出的红包总额不能超过多少元?
参考答案
1.C
2.D
3.C
4.A
5.C
6.B
7.B
8.B
9.D
10.A
11.C
12.A
13.A
14.
15.
16.4
18.218,225,232
19.,整数解是
解:
由①解得:
由②解得:
所以不等式组的解集为
其中是整数的解为0,1.
20.(1)移项得:x≥2 1
即x≥1
故答案为:x≥1
(2)移项得:
合并同类项得:
系数化为1得:x≤2
故答案为:x≤2
(3)把不等式①和②的解集在数轴上表示出来如下图所示:
(4)由上图知,原不等式组的解集为:﹣1 ≤ x≤2
故答案为:﹣1 ≤ x≤2
21.(1)解:
去分母得:,
去括号得:,
移项合并得:,
∴不等式的解集为,
在数轴上表示为:
(2)解:,
解不等式得,,
解不等式得,,
∴不等式组的解集为.
22.(1)解:设服装店购进种款式的衬衫件,购进种款式的衬衫件,
由题意得:,
解得,
答:服装店购进种款式的衬衫30件,购进种款式的衬衫20件.
(2)解:设服装店购进种款式的衬衫件,则购进种款式的衬衫件,
由题意得:,
解得,
因为为正整数,
所以的所有可能取值为,
当时,总利润为(元),
当时,总利润为(元),
当时,总利润为(元),
答:共有3种购进方案,利润最大的购进方案是购进种款式的衬衫10件,购进种款式的衬衫20件.
23.(1)解:设A款饰品的进价是x元,B款饰品的进价是y元,根据题意,得
,解得:,
答:A,B两款饰品的进价分别是15元,20元;
(2)解:设购进A款饰品m个,则购进B款饰品(100-m)个,根据题意,得
,解得:60≤m≤62,
当m=60时,100-m=40,
当m=61时,100-m=39,
当m=62时,100-m=38,
∴共有3种方案,
方案一:设购进A款饰品60个,购进B款饰品40个;
方案二:设购进A款饰品61个,购进B款饰品39个;
方案三:设购进A款饰品62个,购进B款饰品38个;
答:他有哪3种购进方案,方案一:设购进A款饰品60个,购进B款饰品40个;方案二:设购进A款饰品61个,购进B款饰品39个;方案三:设购进A款饰品62个,购进B款饰品38个;
(3)解:∵按方案一,获得利润为:60(21-15)+40(27-20)=640(元),
按方案二,获得利润为:61(21-15)+39(27-20)=639(元),
按方案三,获得利润为:62(21-15)+38(27-20)=638(元),
∴他是按按方案一进货,
设他给出的红包总额为p元,根据题意,得
,
解得:p≤45,
答:他给出的红包总额不能超过45元.
