人教A版(2019)必修第一册 5.7 三角函数的应用 同步练习卷(含解析)
文档属性
| 名称 | 人教A版(2019)必修第一册 5.7 三角函数的应用 同步练习卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 273.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修第一册《5.7 三角函数的应用》2023年同步练习卷
一、选择题
1.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量由函数F(t)=50+4sin(其中t∈R,0≤t≤20)给出,F(t)的单位是辆/分,t的单位是分,则在下列哪个时间段内车流量是增加的( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
2.已知某人的血压满足函数解析式f(t)=24sin160πt+115,其中f(t)为血压(单位:mmHg),t为时间(单位:min),则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
3.如图所示,一个单摆以OA为始边,OB为终边的角θ(﹣π<θ<π)与时间t(s)满足函数关系式θ=sin(2t+),则当t=0时,角θ的大小及单摆频率是( )
A., B.2, C.,π D.2,π
4.在两个弹簧上各有一个质量分别为M1和M2的小球做上下自由振动,已知它们在时间t(s)离开平衡位置的位移s1(cm)和s2(cm)分别由下列两式确定:,s2=10cos2t.当t=时,s1与s2的大小关系是( )
A.s1>s2 B.s1<s2 C.s1=s2 D.不能确定
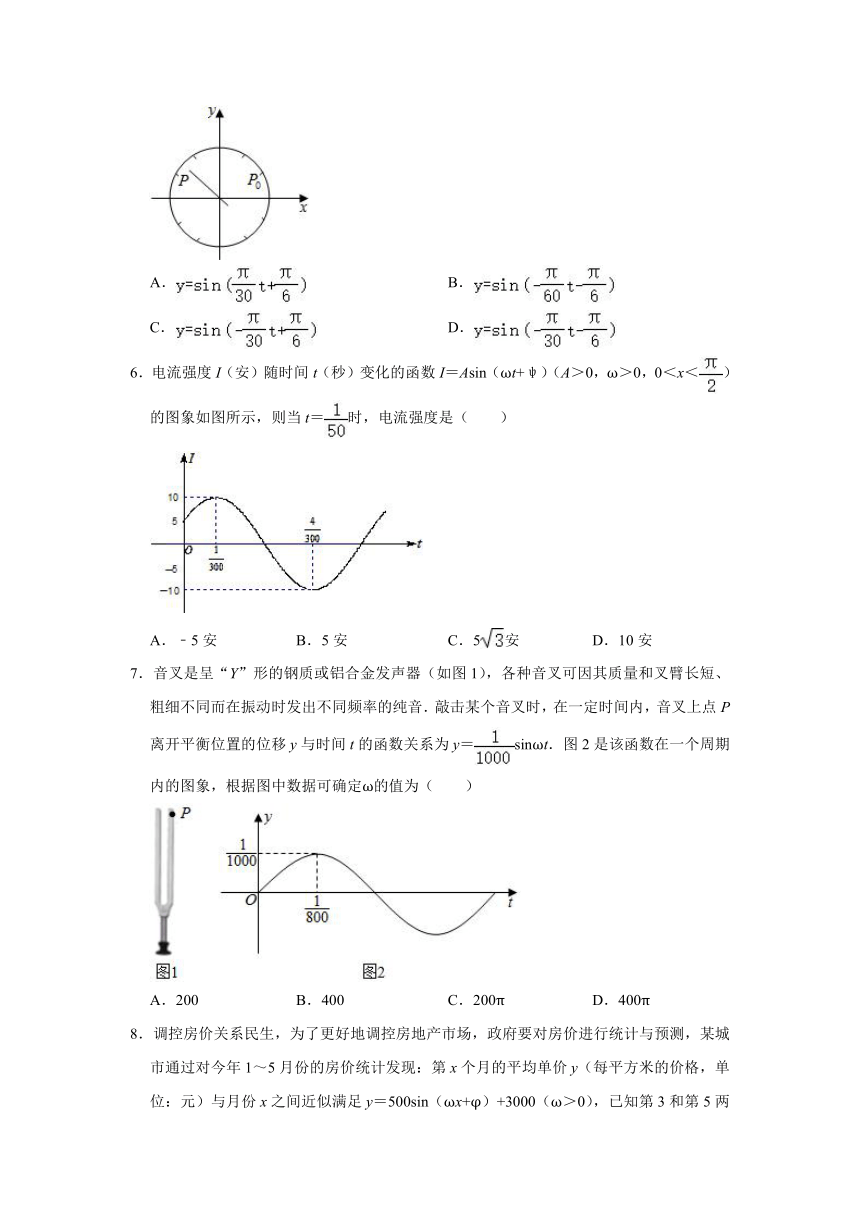
5.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A. B.
C. D.
6.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+ψ)(A>0,ω>0,0<x<)的图象如图所示,则当t=时,电流强度是( )
A.﹣5安 B.5安 C.5安 D.10安
7.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为y=sinωt.图2是该函数在一个周期内的图象,根据图中数据可确定ω的值为( )
A.200 B.400 C.200π D.400π
8.调控房价关系民生,为了更好地调控房地产市场,政府要对房价进行统计与预测,某城市通过对今年1~5月份的房价统计发现:第x个月的平均单价y(每平方米的价格,单位:元)与月份x之间近似满足y=500sin(ωx+φ)+3000(ω>0),已知第3和第5两个月的平均单价如表所示,则预测该城市7月份房价的平均单价大约是( )
x 3 5 7
y 3500 3000 ?
A.3500 B.3000 C.2500 D.2000
二、多选题
(多选)9.摩天轮常被当作一个城市的地标性建筑,如武汉东湖的“东湖之眼”摩天轮,如图所示,某摩天轮最高点离地面高度55米,转盘直径为50米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针方向匀速旋转t分钟,当t=10时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为5米
B.若旋转t分钟后,游客距离地面的高度为h米,则
C.存在t1,t2∈[0,15],使得游客在该时刻距离地面的高度均为20米
D.若在t1,t2时刻游客距离地面的高度相等,则t1+t2的最小值为20
三、填空题
10.函数y=Asin(ωx+φ)(A>0,ω>0)的振幅是3,最小正周期是,初相是2,则它的解析式为 .
11.电流强度I(安培)随时间t(秒)变化的函数I=Asin(ωt+φ)的图象如图所示,则秒时的电流强度为 .
12.电流I(A)随时间t(s)变化的关系式是I=5sin(100πt+),则当t=时,电流为 A.
13.如图是一半径为2米的水轮,水轮的圆心O距离水面1米,已知水轮自点M开始以1分钟旋转4圈的速度顺时针旋转,点M距水面的高度y(米)与时间x(秒)满足函数关系式y=Asin(ωx+φ)+1(A>0,ω>0,),则A= ,ω= .
14.国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω的最小值= .
四、解答题
15.据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈f(x)=Asin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元;该商品每件的售价为g(x)(x为月份),且满足g(x)=f(x﹣2)+2.
(1)分别写出该商品每件的出厂价函数f(x)、售价函数g(x)的解析式;
(2)问哪几个月能盈利?
16.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
时刻(t) 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深/米(y) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
(1)若用函数f(t)=Asin(ωt+φ)+h(A>0,ω>0,|φ|<)来近似描述这个港口的水深和时间之间的对应关系,根据表中数据确定函数表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定要有2.25米的安全间隙(船底与洋底的距离),该船何时能进入港口?
参考答案与试题解析
一、选择题
1.【解答】解:本题即求函数F(t)=50+4sin的增区间,
由,k∈z,解得 4kπ﹣π≤t≤4kπ+π,
故函数F(t)=50+4sin的增区间为[4kπ﹣π,4kπ+π],k∈z,
结合所给的选项,只有选项C中的区间是[4kπ﹣π,4kπ+π],k∈z的子区间,
故选:C.
2.【解答】解:∵人的血压满足函数解析式f(t)=24sin160πt+115,
其中f(t)为血压(单位:mmHg),t为时间(单位:min),
∴T==,
∴=80.
故选:C.
3.【解答】解:由题意,当t=0时,θ=sin()=;
由函数的解析式可知,函数的周期为,故单摆频率为
故选:A.
4.【解答】解:根据题意,当t=时,S1=5sin(2×+)=5sin=﹣5,
s2=10cos=﹣10cos=﹣5,
则有S1=S2,
故选:C.
5.【解答】解:∵秒针是顺时针旋转,
∴角速度ω<0.又由每60秒转一周,
∴ω=﹣=﹣(弧度/秒),
由P0(,),得,cosφ=,sinφ=.
解得φ=,
故选:C.
6.【解答】解:由函数图象可知函数的最大值为10,最小值为﹣10,
又由A>0,∴A=10,
,
由 ,
∴I=10sin(100πt+φ),
当 时,,
∴,
当 时,I=5.
故选:B.
7.【解答】解:由y与t的函数关系为y=sinωt,且T=,
所以T=,所以ω==400π.
故选:D.
8.【解答】解:由题意可得:3500=500sin(3ω+φ)+3000(ω>0),3000=500sin(5ω+φ)+3000(ω>0),
化为:sin(3ω+φ)=1(ω>0),sin(5ω+φ)=0,
可得:3ω+φ=2k1,5ω+φ=2k2π,k1,k2∈Z.
取ω=(k2﹣k1)π﹣,取k2﹣k1=1.
则ω=,取φ=.
∴y=f(x)=500sin(x+)+3000(ω>0),
∴f(7)=500sin(×7+)+3000=2500.
故选:C.
二、多选题
9.【解答】解:由题意可得A正确;
又因为半个周期=10,即T=20=,解得ω=π,
旋转t分钟后,游客距离地面的高度为h米,设h=Acos(ωt)+b,
由题意可得|A|+b=55,﹣|A|+b=5,解得|A|=25,b=30,
而转动10分钟时,达到最高处,即55=Acos( 10)+30,可得A=﹣25,
所以函数h=﹣25cos(t)+30,所以B正确;
C中,由B可知,假设存在t1,t2∈[0,15],又高度相等,可得对称轴t=10,即=10,
令0≤t≤π,可得0≤t≤10,
令π≤t≤2π,可得10≤t≤20,
则h在[0,10]单调递增,在[10,15]上单调递减,当t=10时,hmax=55,
当t=0时,h=5;当t=15时,h=﹣25cos(π)+30=30>20,
所以h=20在t∈[0,15]只有一个解,与两个解矛盾,即假设不成立,所以C不正确;
D中,函数h的周期T=20,由余弦函数的性质可得,令t=kπ,则t=10k,k∈N+,
即函数h关于t=10k对称,若t1,t2时刻游客距离地面的高度相等,
当k=1时=10,即t1+t2的最小值为20,所以D正确.
故选:ABD.
三、填空题
10.【解答】解:∵函数y=Asin(ωx+φ)(A>0,ω>0)的振幅是A=3,
最小正周期是 =,∴ω=5..
∵初相是φ=2,故它的解析式为y=3sin(5x+2),
故答案为:y=3sin(5x+2).
11.【解答】解:根据函数I=Asin(ωt+φ)的图象,可得A=10,==﹣,
∴ω=100π,
再根据五点法作图可得100π +φ=,求得φ=,∴I=10sin(100πt+),
令t=,求得I=10sinπ=0,
故答案为:0.
12.【解答】解:在I=5sin(100πt+)中,取t=,
可得I=5sin(100π×+)=5sin()=5cos==2.5.
故答案为:2.5.
13.【解答】解:∵水轮的半径为2,水轮圆心O距离水面1,
A=3,
又水轮每分钟旋转4圈,故转一圈需要15秒,
∴T=15=,
∴ω=,
故答案为:3,
14.【解答】解:因为国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+)+60(美元)[t(天),A>0,ω>0],最高油价80美元,所以80=Asin(ωπt+)+60,因为sin(ωπt+)≤1,所以A=20,
当t=150(天)时达到最低油价,即sin(150ωπ+)=﹣1,
此时150ωπ+=2kπ﹣,k∈Z,
因为ω>0,所以令k=1,150ωπ+=2π﹣,
解得ω=.
故答案为:.
四、解答题
15.【解答】解:(1)f(x)=Asin(ωx+φ)+B,由题意可得A=2,
B=6,ω=,φ=﹣,
所以f(x)=2sin(x﹣)+6(1≤x≤12,x为正整数),
g(x)=2sin(x﹣π)+8(1≤x≤12,x为正整数).
(2)由g(x)>f(x),得sinx<.
2kπ+π<x<2kπ+π,k∈Z,
∴8k+3<x<8k+9,k∈Z,
∵1≤x≤12,k∈Z,∴k=0时,3<x<9,
∴x=4,5,6,7,8;
k=1时,11<x<17,∴x=12.
∴x=4,5,6,7,8,12.
即其中4,5,6,7,8,12月份能盈利.
16.【解答】解:(1)水深和时间之间的对应关系,周期T=12.
∴ω=,
可知A=,
h=.
∴f(t)=sin(ωt+φ)+5.
当t=3时f(3)=7.5.
即sin(3×+φ)=1.
∵|φ|<,
∴φ=0.
∴函数表达式为∴f(t)=sint+5.(0<t≤24)
(2)船底与水面的距离为4米,船底与洋底的距离2.25米,
∴y≥6.25,即sint+5≥6.25
可得sint.
∴+2kπ≥+2kπ,k∈Z.
解得:1≤t≤5或13≤t≤17.
故得该船1≤t≤5或13≤t≤17.能进入港口满足安全要求.
一、选择题
1.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量由函数F(t)=50+4sin(其中t∈R,0≤t≤20)给出,F(t)的单位是辆/分,t的单位是分,则在下列哪个时间段内车流量是增加的( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
2.已知某人的血压满足函数解析式f(t)=24sin160πt+115,其中f(t)为血压(单位:mmHg),t为时间(单位:min),则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
3.如图所示,一个单摆以OA为始边,OB为终边的角θ(﹣π<θ<π)与时间t(s)满足函数关系式θ=sin(2t+),则当t=0时,角θ的大小及单摆频率是( )
A., B.2, C.,π D.2,π
4.在两个弹簧上各有一个质量分别为M1和M2的小球做上下自由振动,已知它们在时间t(s)离开平衡位置的位移s1(cm)和s2(cm)分别由下列两式确定:,s2=10cos2t.当t=时,s1与s2的大小关系是( )
A.s1>s2 B.s1<s2 C.s1=s2 D.不能确定
5.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
A. B.
C. D.
6.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+ψ)(A>0,ω>0,0<x<)的图象如图所示,则当t=时,电流强度是( )
A.﹣5安 B.5安 C.5安 D.10安
7.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为y=sinωt.图2是该函数在一个周期内的图象,根据图中数据可确定ω的值为( )
A.200 B.400 C.200π D.400π
8.调控房价关系民生,为了更好地调控房地产市场,政府要对房价进行统计与预测,某城市通过对今年1~5月份的房价统计发现:第x个月的平均单价y(每平方米的价格,单位:元)与月份x之间近似满足y=500sin(ωx+φ)+3000(ω>0),已知第3和第5两个月的平均单价如表所示,则预测该城市7月份房价的平均单价大约是( )
x 3 5 7
y 3500 3000 ?
A.3500 B.3000 C.2500 D.2000
二、多选题
(多选)9.摩天轮常被当作一个城市的地标性建筑,如武汉东湖的“东湖之眼”摩天轮,如图所示,某摩天轮最高点离地面高度55米,转盘直径为50米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针方向匀速旋转t分钟,当t=10时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为5米
B.若旋转t分钟后,游客距离地面的高度为h米,则
C.存在t1,t2∈[0,15],使得游客在该时刻距离地面的高度均为20米
D.若在t1,t2时刻游客距离地面的高度相等,则t1+t2的最小值为20
三、填空题
10.函数y=Asin(ωx+φ)(A>0,ω>0)的振幅是3,最小正周期是,初相是2,则它的解析式为 .
11.电流强度I(安培)随时间t(秒)变化的函数I=Asin(ωt+φ)的图象如图所示,则秒时的电流强度为 .
12.电流I(A)随时间t(s)变化的关系式是I=5sin(100πt+),则当t=时,电流为 A.
13.如图是一半径为2米的水轮,水轮的圆心O距离水面1米,已知水轮自点M开始以1分钟旋转4圈的速度顺时针旋转,点M距水面的高度y(米)与时间x(秒)满足函数关系式y=Asin(ωx+φ)+1(A>0,ω>0,),则A= ,ω= .
14.国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω的最小值= .
四、解答题
15.据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈f(x)=Asin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元;该商品每件的售价为g(x)(x为月份),且满足g(x)=f(x﹣2)+2.
(1)分别写出该商品每件的出厂价函数f(x)、售价函数g(x)的解析式;
(2)问哪几个月能盈利?
16.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
时刻(t) 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深/米(y) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
(1)若用函数f(t)=Asin(ωt+φ)+h(A>0,ω>0,|φ|<)来近似描述这个港口的水深和时间之间的对应关系,根据表中数据确定函数表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定要有2.25米的安全间隙(船底与洋底的距离),该船何时能进入港口?
参考答案与试题解析
一、选择题
1.【解答】解:本题即求函数F(t)=50+4sin的增区间,
由,k∈z,解得 4kπ﹣π≤t≤4kπ+π,
故函数F(t)=50+4sin的增区间为[4kπ﹣π,4kπ+π],k∈z,
结合所给的选项,只有选项C中的区间是[4kπ﹣π,4kπ+π],k∈z的子区间,
故选:C.
2.【解答】解:∵人的血压满足函数解析式f(t)=24sin160πt+115,
其中f(t)为血压(单位:mmHg),t为时间(单位:min),
∴T==,
∴=80.
故选:C.
3.【解答】解:由题意,当t=0时,θ=sin()=;
由函数的解析式可知,函数的周期为,故单摆频率为
故选:A.
4.【解答】解:根据题意,当t=时,S1=5sin(2×+)=5sin=﹣5,
s2=10cos=﹣10cos=﹣5,
则有S1=S2,
故选:C.
5.【解答】解:∵秒针是顺时针旋转,
∴角速度ω<0.又由每60秒转一周,
∴ω=﹣=﹣(弧度/秒),
由P0(,),得,cosφ=,sinφ=.
解得φ=,
故选:C.
6.【解答】解:由函数图象可知函数的最大值为10,最小值为﹣10,
又由A>0,∴A=10,
,
由 ,
∴I=10sin(100πt+φ),
当 时,,
∴,
当 时,I=5.
故选:B.
7.【解答】解:由y与t的函数关系为y=sinωt,且T=,
所以T=,所以ω==400π.
故选:D.
8.【解答】解:由题意可得:3500=500sin(3ω+φ)+3000(ω>0),3000=500sin(5ω+φ)+3000(ω>0),
化为:sin(3ω+φ)=1(ω>0),sin(5ω+φ)=0,
可得:3ω+φ=2k1,5ω+φ=2k2π,k1,k2∈Z.
取ω=(k2﹣k1)π﹣,取k2﹣k1=1.
则ω=,取φ=.
∴y=f(x)=500sin(x+)+3000(ω>0),
∴f(7)=500sin(×7+)+3000=2500.
故选:C.
二、多选题
9.【解答】解:由题意可得A正确;
又因为半个周期=10,即T=20=,解得ω=π,
旋转t分钟后,游客距离地面的高度为h米,设h=Acos(ωt)+b,
由题意可得|A|+b=55,﹣|A|+b=5,解得|A|=25,b=30,
而转动10分钟时,达到最高处,即55=Acos( 10)+30,可得A=﹣25,
所以函数h=﹣25cos(t)+30,所以B正确;
C中,由B可知,假设存在t1,t2∈[0,15],又高度相等,可得对称轴t=10,即=10,
令0≤t≤π,可得0≤t≤10,
令π≤t≤2π,可得10≤t≤20,
则h在[0,10]单调递增,在[10,15]上单调递减,当t=10时,hmax=55,
当t=0时,h=5;当t=15时,h=﹣25cos(π)+30=30>20,
所以h=20在t∈[0,15]只有一个解,与两个解矛盾,即假设不成立,所以C不正确;
D中,函数h的周期T=20,由余弦函数的性质可得,令t=kπ,则t=10k,k∈N+,
即函数h关于t=10k对称,若t1,t2时刻游客距离地面的高度相等,
当k=1时=10,即t1+t2的最小值为20,所以D正确.
故选:ABD.
三、填空题
10.【解答】解:∵函数y=Asin(ωx+φ)(A>0,ω>0)的振幅是A=3,
最小正周期是 =,∴ω=5..
∵初相是φ=2,故它的解析式为y=3sin(5x+2),
故答案为:y=3sin(5x+2).
11.【解答】解:根据函数I=Asin(ωt+φ)的图象,可得A=10,==﹣,
∴ω=100π,
再根据五点法作图可得100π +φ=,求得φ=,∴I=10sin(100πt+),
令t=,求得I=10sinπ=0,
故答案为:0.
12.【解答】解:在I=5sin(100πt+)中,取t=,
可得I=5sin(100π×+)=5sin()=5cos==2.5.
故答案为:2.5.
13.【解答】解:∵水轮的半径为2,水轮圆心O距离水面1,
A=3,
又水轮每分钟旋转4圈,故转一圈需要15秒,
∴T=15=,
∴ω=,
故答案为:3,
14.【解答】解:因为国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+)+60(美元)[t(天),A>0,ω>0],最高油价80美元,所以80=Asin(ωπt+)+60,因为sin(ωπt+)≤1,所以A=20,
当t=150(天)时达到最低油价,即sin(150ωπ+)=﹣1,
此时150ωπ+=2kπ﹣,k∈Z,
因为ω>0,所以令k=1,150ωπ+=2π﹣,
解得ω=.
故答案为:.
四、解答题
15.【解答】解:(1)f(x)=Asin(ωx+φ)+B,由题意可得A=2,
B=6,ω=,φ=﹣,
所以f(x)=2sin(x﹣)+6(1≤x≤12,x为正整数),
g(x)=2sin(x﹣π)+8(1≤x≤12,x为正整数).
(2)由g(x)>f(x),得sinx<.
2kπ+π<x<2kπ+π,k∈Z,
∴8k+3<x<8k+9,k∈Z,
∵1≤x≤12,k∈Z,∴k=0时,3<x<9,
∴x=4,5,6,7,8;
k=1时,11<x<17,∴x=12.
∴x=4,5,6,7,8,12.
即其中4,5,6,7,8,12月份能盈利.
16.【解答】解:(1)水深和时间之间的对应关系,周期T=12.
∴ω=,
可知A=,
h=.
∴f(t)=sin(ωt+φ)+5.
当t=3时f(3)=7.5.
即sin(3×+φ)=1.
∵|φ|<,
∴φ=0.
∴函数表达式为∴f(t)=sint+5.(0<t≤24)
(2)船底与水面的距离为4米,船底与洋底的距离2.25米,
∴y≥6.25,即sint+5≥6.25
可得sint.
∴+2kπ≥+2kπ,k∈Z.
解得:1≤t≤5或13≤t≤17.
故得该船1≤t≤5或13≤t≤17.能进入港口满足安全要求.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
