5.5 应用二元一次方程组-里程碑上的数 课件(共23张PPT)-2023-2024学年八年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 5.5 应用二元一次方程组-里程碑上的数 课件(共23张PPT)-2023-2024学年八年级数学上册同步精品课堂(北师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 12:01:56 | ||
图片预览








文档简介
(共23张PPT)
北师大版 数学 八年级上册
第五章 二元一次方程组
5 应用二元一次方程组--里程碑上的数
学习目标
1.利用二元一次方程解决数字问题和行程问题.
(重点)
2.进一步经历和体验列方程组解决实际问题的过程.
复习回顾
1.一个两位数,十位数字是x,个位数字是y,那么这个数可表示为______.
2.一个三位数,百位数字是a,十位数字为b,个位数字十c,则这个三位数可表示为___________ .
4.a是一个两位数,b 是一个三位数,若把a放在b 的左边得到一个五位数,则这个五位数可表示为______________.
3.一个两位数,十位数字是a,个位数字为b,若在这个两位数中间加1个0,得到一个三位数,则这个三位数可表示为___________.
试表示下列数:
10x+y
100a+10b+c
100a+b
1000a+b
一、创设情境,引入新知
观察下列图片:你认识这是什么吗?是用来干什么的?
里程碑(解释: 路边标志里数的碑。)
指的是标志公路及城市郊区道路里程的碑石。每一公里设一块,用以计算里程和标志地点位置。
二、自主合作,探究新知
探究一:利用二元一次方程组解决数字问题
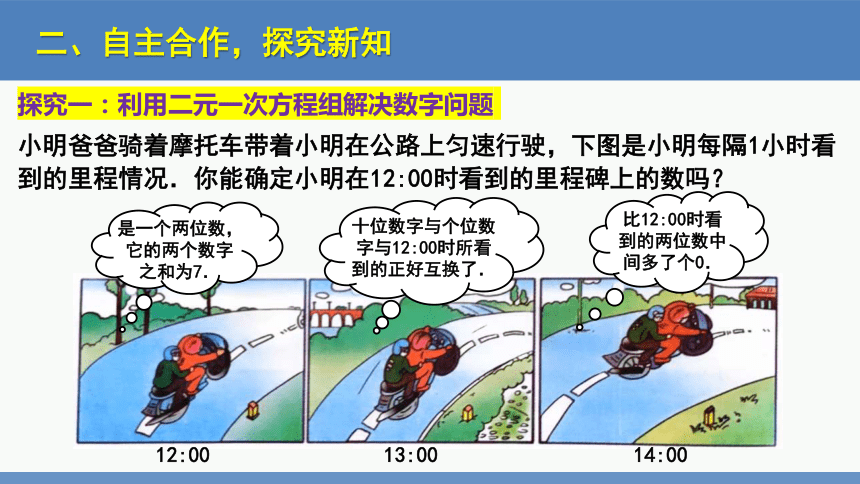
小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
12:00 13:00 14:00
是一个两位数,它的两个数字之和为7.
十位数字与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
(3)14:00时小明看到的数可以表示为____________,
13:00-14:00间摩托车行驶的路程是__________________;
(1)12:00时小明看到的数可以表示为____________,
根据两个数字之和是7,可列出方程____________;
(2)13:00时小明看到的数可以表示为_____________,
12:00-13:00间摩托车行驶的路程是_________________;
二、自主合作,探究新知
(4)12:00~13:00与13:00~14:00两段时间内行驶的路程有什么关系 你能列出相应的方程吗
100x+y
分析:如果设小明在12:00时看到的数的十位数字是x,个位数字是y.那么
10x+y
10y+x
x+y=7
(100x+y)-(10y+x)
(10y+x)-(10x+y)
二、自主合作,探究新知
12:00至13:00所走的路程 13:00至14:00所走的路程
(10y+x)-(10x+y)
(100x+y)-(10y+x)
=
解:设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
答:小明在12:00时看到的里程碑上的数是16.
解这个方程组得,
二、自主合作,探究新知
1.在求两位数或三位数时,一般是不能直接设这个两位数或三位数的,而是把它各个数位上的数字设为未知数.
2.解题的关键是弄清题意,根据题意找出合适的等量关系,列出方程组,再进行求解.
知识要点
二、自主合作,探究新知
解:设十位上的数字为x,个位上的数字为y.
例1:一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
检验:56-3(5+6)=23
56÷(5+6)=5…1
典型例题
∴10x+y=56.
答:原来的两位数为56.
解得
x=5
y=6
根据题意,得
(10x+y)-3(x+y)=23
10x+y=5(x+y)+1
二、自主合作,探究新知
例2:两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2 178, 求这两个两位数.
分析:设较大的两位数为x,较小的两位数为y.
在较大数的右边接着写较小的数,所写的数可表示为 ;
在较大数的左边写上较小的数,所写的数可表示为 .
典型例题
10x+y
100y+x
此问题中的两位数是一个“整体”
二、自主合作,探究新知
解:设较大的两位数为x,较小的两位数为y.
答:这两个两位数分别是45和23.
解这个方程组,得:
x=45
y=23
x+y=68
(100x+y)-(100y+x)=2178
根据题意,得
x+y=68
99x-99y=2178
化简,得
x+y=68
x-y=22
即
二、自主合作,探究新知
议一议:
列二元一次方程组解决实际问题的一般步骤是怎样的?与同伴进行交流.
(1)弄清题意和题目中的等量关系.用字母表示题目中的两个未知数;
(2)找出能够表示应用题全部含义的两个相等关系;
(3)根据这两个相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组并求出未知数的值;
(5)根据应用题的实际意义,检查求得的结果是否合理;
(6)写出符合题意的解释.
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
二、自主合作,探究新知
探究二:利用二元一次方程组解决行程问题
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=_____,
走上坡的时间+走平路的时间=_____.
10
15
二、自主合作,探究新知
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
二、自主合作,探究新知
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
∴平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
方法二(间接设元法)
三、即学即练,应用知识
1.小颖家离学校4800 m,其中有一段为上坡路 ,另一段为下坡路,她跑步去学校共用了30 min .已知小颖在上坡时的平均速度是 6 km/h,下坡时的平均速度是12 km/h.问小颖上、下坡的路程分别是( )
A.1.2 km,3.6 km; B.1.8 km,3 km;
C.1.6 km,3.2 km. D.3.2 km,1.6 km.
A
2.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数是 .
18
三、即学即练,应用知识
解:设原来的两个加数分别是x,y.
答:原来的两个加数分别是21,32.
3.小明和小亮做加法游戏.小明在一个加数后面多写了一个 0,得到的和为 242;而小亮在另一个加数后面多写了一个0,得到的和为 341. 原来的两个加数分别是多少
根据题意,得
10x+y=242
x+10y=341
x=21
y=32
解得
三、即学即练,应用知识
4. 一个两位数,个位上的数字与十位上的数字之和是11,如果把十位上的数字与个位上的数字对调,那么所得的两位数比原两位数大9,求原来的两位数.
解:设个位上的数字为x,十位上的数字为y.
答:原来的两位数为56.
10y+x=56.
x=6
y=5
解得
根据题意,得
x+y=11
10x+y=10y+x+9
四、课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
2.这种处理问题的过程可以进一步概括为:
1.一个两位数,十位数字比个位数字的两倍大一若将这个两位数减去36,恰好等于个位数字与十位数字对调后所得的两位数。则这个两位数是( )
A.86 B.68 C.97 D.73
五、当堂达标检测
2.已知某歌曲中歌词的字数是一个两位数,十位数字是个位数字的两倍,且十位数字比个位数字大4,则这首歌曲中歌词有 个字.
D
84
五、当堂达标检测
3.一个两位数是另一个两位数的3倍,如果把这个两位数放在另一个两位数的左边与放在右边所得的数之和为8484.求这个两位数.
答:这个两位数是63,另一个两位数是21.
解:设这个两位数为x,另一个为y.
解这个方程组,得
x=63
y=21
由题意,得
x=3y
(100x+y)+(100y+x)=8484
五、当堂达标检测
4.小颖家离学校1880米,其中有一段为上坡路,另一段为下坡路,她跑步去学校,共用了16min.已知小影在上坡路上的平均速度是4.8km/h,在下坡路上的平均速度是12km/h,小颖上坡、下坡各用了多长时间?
解:设小颖上坡用了x min,下坡用了y min.
答:小颖上坡用了11min,下坡用了5min.
4.8km/h=80m/min,12km/h=200m/min.
根据题意,得:
x+y=16
80x+200y=1880
解方程组,得
x=11
y=5
教材习题5.6;
六、布置作业
北师大版 数学 八年级上册
第五章 二元一次方程组
5 应用二元一次方程组--里程碑上的数
学习目标
1.利用二元一次方程解决数字问题和行程问题.
(重点)
2.进一步经历和体验列方程组解决实际问题的过程.
复习回顾
1.一个两位数,十位数字是x,个位数字是y,那么这个数可表示为______.
2.一个三位数,百位数字是a,十位数字为b,个位数字十c,则这个三位数可表示为___________ .
4.a是一个两位数,b 是一个三位数,若把a放在b 的左边得到一个五位数,则这个五位数可表示为______________.
3.一个两位数,十位数字是a,个位数字为b,若在这个两位数中间加1个0,得到一个三位数,则这个三位数可表示为___________.
试表示下列数:
10x+y
100a+10b+c
100a+b
1000a+b
一、创设情境,引入新知
观察下列图片:你认识这是什么吗?是用来干什么的?
里程碑(解释: 路边标志里数的碑。)
指的是标志公路及城市郊区道路里程的碑石。每一公里设一块,用以计算里程和标志地点位置。
二、自主合作,探究新知
探究一:利用二元一次方程组解决数字问题
小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
12:00 13:00 14:00
是一个两位数,它的两个数字之和为7.
十位数字与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
(3)14:00时小明看到的数可以表示为____________,
13:00-14:00间摩托车行驶的路程是__________________;
(1)12:00时小明看到的数可以表示为____________,
根据两个数字之和是7,可列出方程____________;
(2)13:00时小明看到的数可以表示为_____________,
12:00-13:00间摩托车行驶的路程是_________________;
二、自主合作,探究新知
(4)12:00~13:00与13:00~14:00两段时间内行驶的路程有什么关系 你能列出相应的方程吗
100x+y
分析:如果设小明在12:00时看到的数的十位数字是x,个位数字是y.那么
10x+y
10y+x
x+y=7
(100x+y)-(10y+x)
(10y+x)-(10x+y)
二、自主合作,探究新知
12:00至13:00所走的路程 13:00至14:00所走的路程
(10y+x)-(10x+y)
(100x+y)-(10y+x)
=
解:设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
答:小明在12:00时看到的里程碑上的数是16.
解这个方程组得,
二、自主合作,探究新知
1.在求两位数或三位数时,一般是不能直接设这个两位数或三位数的,而是把它各个数位上的数字设为未知数.
2.解题的关键是弄清题意,根据题意找出合适的等量关系,列出方程组,再进行求解.
知识要点
二、自主合作,探究新知
解:设十位上的数字为x,个位上的数字为y.
例1:一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
检验:56-3(5+6)=23
56÷(5+6)=5…1
典型例题
∴10x+y=56.
答:原来的两位数为56.
解得
x=5
y=6
根据题意,得
(10x+y)-3(x+y)=23
10x+y=5(x+y)+1
二、自主合作,探究新知
例2:两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2 178, 求这两个两位数.
分析:设较大的两位数为x,较小的两位数为y.
在较大数的右边接着写较小的数,所写的数可表示为 ;
在较大数的左边写上较小的数,所写的数可表示为 .
典型例题
10x+y
100y+x
此问题中的两位数是一个“整体”
二、自主合作,探究新知
解:设较大的两位数为x,较小的两位数为y.
答:这两个两位数分别是45和23.
解这个方程组,得:
x=45
y=23
x+y=68
(100x+y)-(100y+x)=2178
根据题意,得
x+y=68
99x-99y=2178
化简,得
x+y=68
x-y=22
即
二、自主合作,探究新知
议一议:
列二元一次方程组解决实际问题的一般步骤是怎样的?与同伴进行交流.
(1)弄清题意和题目中的等量关系.用字母表示题目中的两个未知数;
(2)找出能够表示应用题全部含义的两个相等关系;
(3)根据这两个相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组并求出未知数的值;
(5)根据应用题的实际意义,检查求得的结果是否合理;
(6)写出符合题意的解释.
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
二、自主合作,探究新知
探究二:利用二元一次方程组解决行程问题
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=_____,
走上坡的时间+走平路的时间=_____.
10
15
二、自主合作,探究新知
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
二、自主合作,探究新知
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
∴平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
方法二(间接设元法)
三、即学即练,应用知识
1.小颖家离学校4800 m,其中有一段为上坡路 ,另一段为下坡路,她跑步去学校共用了30 min .已知小颖在上坡时的平均速度是 6 km/h,下坡时的平均速度是12 km/h.问小颖上、下坡的路程分别是( )
A.1.2 km,3.6 km; B.1.8 km,3 km;
C.1.6 km,3.2 km. D.3.2 km,1.6 km.
A
2.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数是 .
18
三、即学即练,应用知识
解:设原来的两个加数分别是x,y.
答:原来的两个加数分别是21,32.
3.小明和小亮做加法游戏.小明在一个加数后面多写了一个 0,得到的和为 242;而小亮在另一个加数后面多写了一个0,得到的和为 341. 原来的两个加数分别是多少
根据题意,得
10x+y=242
x+10y=341
x=21
y=32
解得
三、即学即练,应用知识
4. 一个两位数,个位上的数字与十位上的数字之和是11,如果把十位上的数字与个位上的数字对调,那么所得的两位数比原两位数大9,求原来的两位数.
解:设个位上的数字为x,十位上的数字为y.
答:原来的两位数为56.
10y+x=56.
x=6
y=5
解得
根据题意,得
x+y=11
10x+y=10y+x+9
四、课堂小结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
2.这种处理问题的过程可以进一步概括为:
1.一个两位数,十位数字比个位数字的两倍大一若将这个两位数减去36,恰好等于个位数字与十位数字对调后所得的两位数。则这个两位数是( )
A.86 B.68 C.97 D.73
五、当堂达标检测
2.已知某歌曲中歌词的字数是一个两位数,十位数字是个位数字的两倍,且十位数字比个位数字大4,则这首歌曲中歌词有 个字.
D
84
五、当堂达标检测
3.一个两位数是另一个两位数的3倍,如果把这个两位数放在另一个两位数的左边与放在右边所得的数之和为8484.求这个两位数.
答:这个两位数是63,另一个两位数是21.
解:设这个两位数为x,另一个为y.
解这个方程组,得
x=63
y=21
由题意,得
x=3y
(100x+y)+(100y+x)=8484
五、当堂达标检测
4.小颖家离学校1880米,其中有一段为上坡路,另一段为下坡路,她跑步去学校,共用了16min.已知小影在上坡路上的平均速度是4.8km/h,在下坡路上的平均速度是12km/h,小颖上坡、下坡各用了多长时间?
解:设小颖上坡用了x min,下坡用了y min.
答:小颖上坡用了11min,下坡用了5min.
4.8km/h=80m/min,12km/h=200m/min.
根据题意,得:
x+y=16
80x+200y=1880
解方程组,得
x=11
y=5
教材习题5.6;
六、布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
