人教版八年级数学上册13.3.1 等腰三角形综合运用 公开课导学案及作业设计(2课时)
文档属性
| 名称 | 人教版八年级数学上册13.3.1 等腰三角形综合运用 公开课导学案及作业设计(2课时) |

|
|
| 格式 | doc | ||
| 文件大小 | 451.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 17:27:04 | ||
图片预览

文档简介
人教版八年级数学上册第十三章
《等腰三角形综合运用》学习任务单及作业设计
(共2课时)
第一课时
【学习目标】
1.进一步理解和掌握等腰三角形的性质与判定,并能综合运用这些知识判断三角形形状和求三角形边角等有关计算及证明。
2.在例题探究过程中培养学生观察、分析和归纳能力,并体验转化和方程等思想的应用。
【课前学习任务】
复习等腰三角形、等边三角形的定义、性质及判定,学习利用以上知识解决三角形中的边角求解等问题,预习新课:等腰三角形综合运用。
【课上学习任务】
学习任务一:知识回顾,复习等腰三角形、等边三角形的定义、性质及判定
1.等腰三角形
2. 等边三角形
学习任务二:知识运用一:利用等腰三角形的判定进行三角形形状的判断
例 已知三角形△ABC 的三边长为 a,b,c,
(1)∠A=70°, ∠B=40°, 则三角形的形状为_________;
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为_________;
(3)当满足(a-b)(b-c)(c-a)=0 时,则三角形的形状为_________;
(4)当满足(a-b)2+(b-c)2+(c-a)2=0 时,则三角形的形状为________.
学习任务三:知识运用二:运用等腰三角形的判定和性质进行边角等有关计算及证明
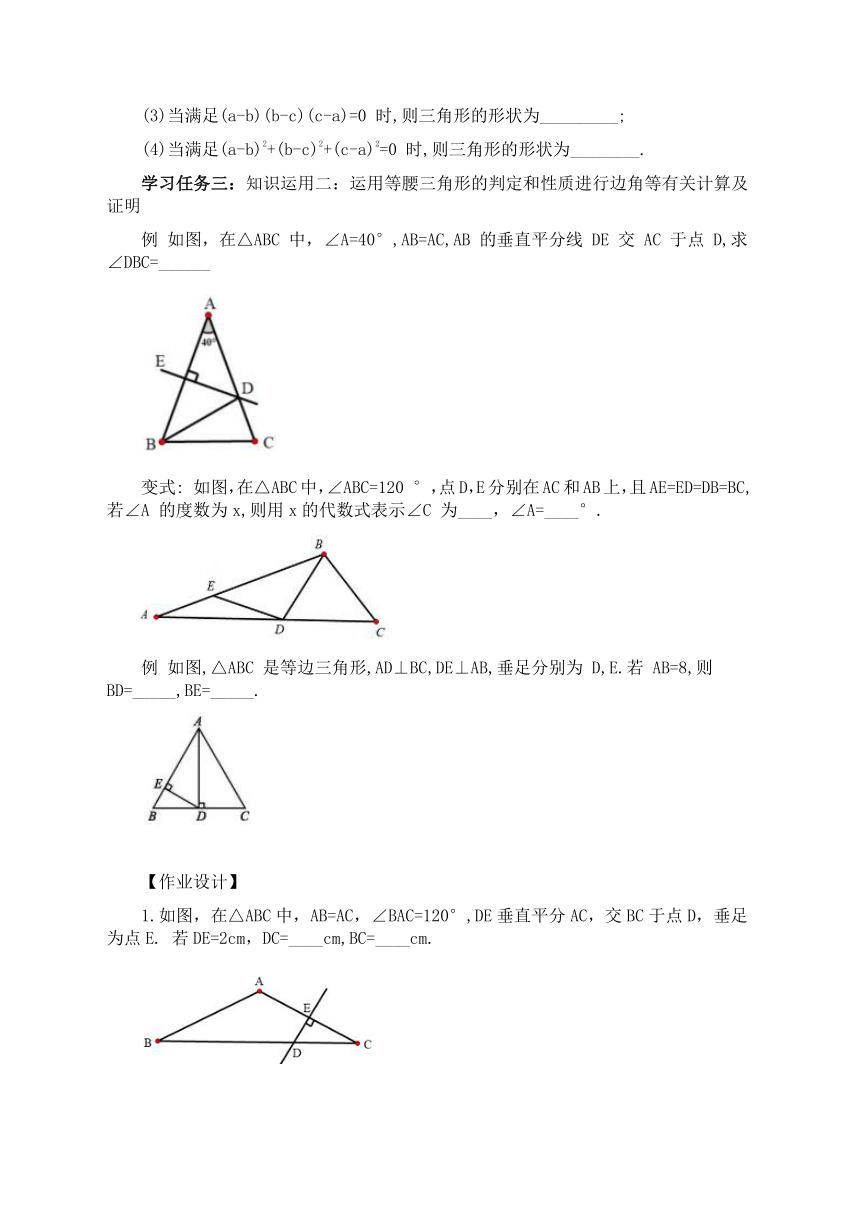
例 如图,在△ABC 中,∠A=40°,AB=AC,AB 的垂直平分线 DE 交 AC 于点 D,求∠DBC=______
变式: 如图,在△ABC中,∠ABC=120 °,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A 的度数为x,则用x的代数式表示∠C 为____,∠A=____°.
例 如图,△ABC 是等边三角形,AD⊥BC,DE⊥AB,垂足分别为 D,E.若 AB=8,则BD=_____,BE=_____.
【作业设计】
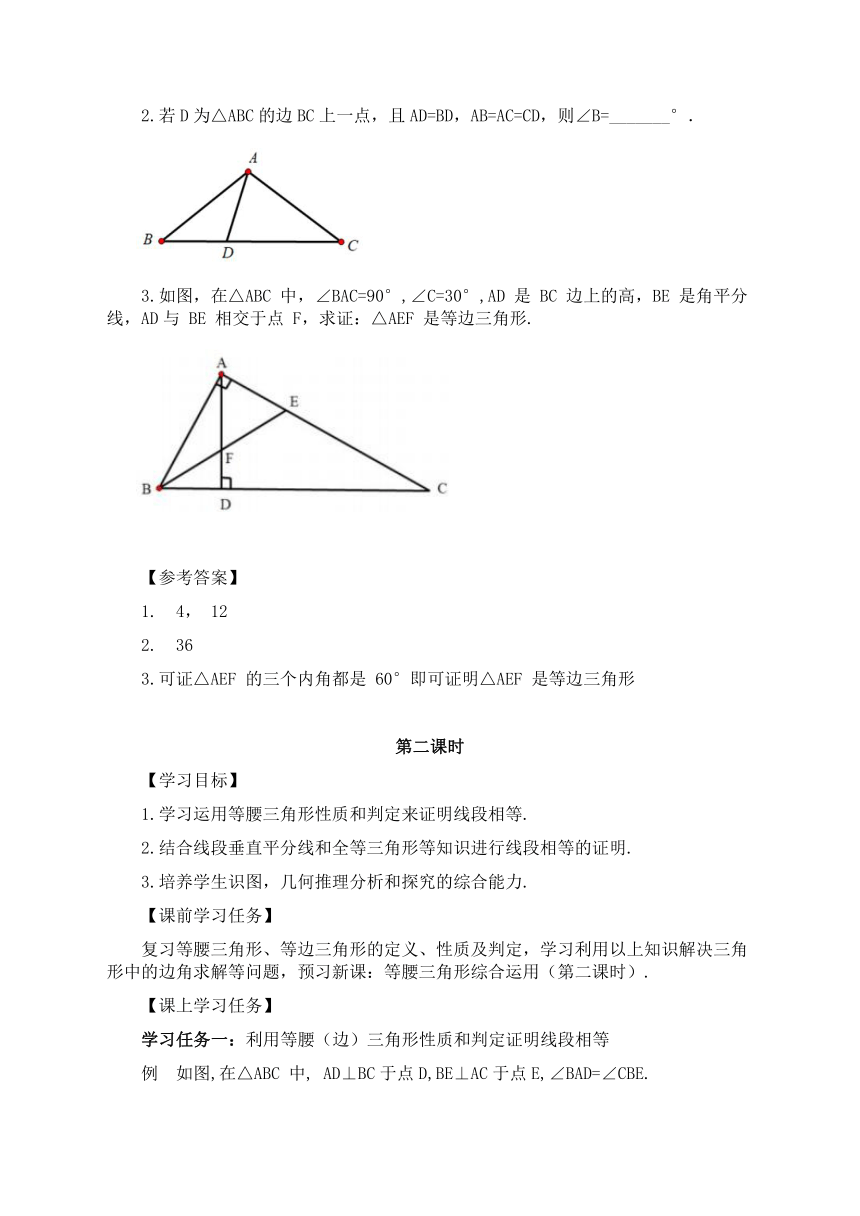
1.如图,在△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC,交BC于点D,垂足为点E. 若DE=2cm,DC=____cm,BC=____cm.
2.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,则∠B=_______°.
3.如图,在△ABC 中,∠BAC=90°,∠C=30°,AD 是 BC 边上的高,BE 是角平分线,AD与 BE 相交于点 F,求证:△AEF 是等边三角形.
【参考答案】
1. 4, 12
2. 36
3.可证△AEF 的三个内角都是 60°即可证明△AEF 是等边三角形
第二课时
【学习目标】
1.学习运用等腰三角形性质和判定来证明线段相等.
2.结合线段垂直平分线和全等三角形等知识进行线段相等的证明.
3.培养学生识图,几何推理分析和探究的综合能力.
【课前学习任务】
复习等腰三角形、等边三角形的定义、性质及判定,学习利用以上知识解决三角形中的边角求解等问题,预习新课:等腰三角形综合运用(第二课时).
【课上学习任务】
学习任务一:利用等腰(边)三角形性质和判定证明线段相等
例 如图,在△ABC 中, AD⊥BC于点D,BE⊥AC于点E,∠BAD=∠CBE.
求证: AB=AC.
学习任务二:利用等腰(边)三角形性质和判定,结合垂直平分线知识,来证明线段相等.
例 如图,在△ABC中,AB=AC,∠ A=120°,ME垂直平分AB于点E,交BC于点M,NF 垂直平分AC于点F,交BC于点N.
求证:BM=MN=CN.
学习任务三:利用等腰(边)三角形性质和判定,结合全等三角形知识,来证明线段相等.
例 如图,点 D,E 在△ABC 的边 BC 上,AB=AC,AD=AE,
求证:BD=CE
例 如图,在△ABC 中,AB=AC,点 D 在 AB 上,点 E 在 AC 的延长线上,且 DB=CE,连接 DE 交BC 于点 F,
求证:DF=EF
【作业设计】
1.已知:如图,AC和BD相交于点O,AB//CD,OA=OB.
求证:OC=OD.
2.如图,在等边三角形△ABC中,∠ABC 和∠ACB 的平分线相交于点O,OB和OC的垂直平分线EE'和 FF'分别交BC于点E和F,连接OE,OF.
证明:AB=3EF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E和F,
(1) 求证:△ABD是等边三角形;
(2) 求证:BE=AF
【参考答案】
1.∵OA=OB,
∴∠A=∠B.
∵AB∥CD,
∴∠A=∠C,∠B=∠D.
∴∠C=∠D.
∴OC=OD.
2.∵△ABC 是等边三角形,
∴∠ABC=∠ACB=60°.
∵OB,OC 是角平分线,
∴∠OBC=∠OCB=30°.
∵EE’和 FF’分别是OB,OC的垂直平分线,
∴EO=EB,FO=FC.
∴∠EBO=∠BOE=30°,∠FOC=∠FCO=30°.
∴∠OEF=∠OFE=60°.
∴△OEF 是等边三角形.
∴OE=EF=OF.
∴BE=EF=CF.
∴AB=3EF.
3.(1)∵AB=AC,AG⊥BC,∠BAC=120°,
∴∠BAD=1/2∠BAC=60°.
∵AB=AD,
∴△ABD 是等边三角形.
(2)证△EBD≌△FAD(ASA)进而得到 BE=AF.
《等腰三角形综合运用》学习任务单及作业设计
(共2课时)
第一课时
【学习目标】
1.进一步理解和掌握等腰三角形的性质与判定,并能综合运用这些知识判断三角形形状和求三角形边角等有关计算及证明。
2.在例题探究过程中培养学生观察、分析和归纳能力,并体验转化和方程等思想的应用。
【课前学习任务】
复习等腰三角形、等边三角形的定义、性质及判定,学习利用以上知识解决三角形中的边角求解等问题,预习新课:等腰三角形综合运用。
【课上学习任务】
学习任务一:知识回顾,复习等腰三角形、等边三角形的定义、性质及判定
1.等腰三角形
2. 等边三角形
学习任务二:知识运用一:利用等腰三角形的判定进行三角形形状的判断
例 已知三角形△ABC 的三边长为 a,b,c,
(1)∠A=70°, ∠B=40°, 则三角形的形状为_________;
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为_________;
(3)当满足(a-b)(b-c)(c-a)=0 时,则三角形的形状为_________;
(4)当满足(a-b)2+(b-c)2+(c-a)2=0 时,则三角形的形状为________.
学习任务三:知识运用二:运用等腰三角形的判定和性质进行边角等有关计算及证明
例 如图,在△ABC 中,∠A=40°,AB=AC,AB 的垂直平分线 DE 交 AC 于点 D,求∠DBC=______
变式: 如图,在△ABC中,∠ABC=120 °,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A 的度数为x,则用x的代数式表示∠C 为____,∠A=____°.
例 如图,△ABC 是等边三角形,AD⊥BC,DE⊥AB,垂足分别为 D,E.若 AB=8,则BD=_____,BE=_____.
【作业设计】
1.如图,在△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC,交BC于点D,垂足为点E. 若DE=2cm,DC=____cm,BC=____cm.
2.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,则∠B=_______°.
3.如图,在△ABC 中,∠BAC=90°,∠C=30°,AD 是 BC 边上的高,BE 是角平分线,AD与 BE 相交于点 F,求证:△AEF 是等边三角形.
【参考答案】
1. 4, 12
2. 36
3.可证△AEF 的三个内角都是 60°即可证明△AEF 是等边三角形
第二课时
【学习目标】
1.学习运用等腰三角形性质和判定来证明线段相等.
2.结合线段垂直平分线和全等三角形等知识进行线段相等的证明.
3.培养学生识图,几何推理分析和探究的综合能力.
【课前学习任务】
复习等腰三角形、等边三角形的定义、性质及判定,学习利用以上知识解决三角形中的边角求解等问题,预习新课:等腰三角形综合运用(第二课时).
【课上学习任务】
学习任务一:利用等腰(边)三角形性质和判定证明线段相等
例 如图,在△ABC 中, AD⊥BC于点D,BE⊥AC于点E,∠BAD=∠CBE.
求证: AB=AC.
学习任务二:利用等腰(边)三角形性质和判定,结合垂直平分线知识,来证明线段相等.
例 如图,在△ABC中,AB=AC,∠ A=120°,ME垂直平分AB于点E,交BC于点M,NF 垂直平分AC于点F,交BC于点N.
求证:BM=MN=CN.
学习任务三:利用等腰(边)三角形性质和判定,结合全等三角形知识,来证明线段相等.
例 如图,点 D,E 在△ABC 的边 BC 上,AB=AC,AD=AE,
求证:BD=CE
例 如图,在△ABC 中,AB=AC,点 D 在 AB 上,点 E 在 AC 的延长线上,且 DB=CE,连接 DE 交BC 于点 F,
求证:DF=EF
【作业设计】
1.已知:如图,AC和BD相交于点O,AB//CD,OA=OB.
求证:OC=OD.
2.如图,在等边三角形△ABC中,∠ABC 和∠ACB 的平分线相交于点O,OB和OC的垂直平分线EE'和 FF'分别交BC于点E和F,连接OE,OF.
证明:AB=3EF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E和F,
(1) 求证:△ABD是等边三角形;
(2) 求证:BE=AF
【参考答案】
1.∵OA=OB,
∴∠A=∠B.
∵AB∥CD,
∴∠A=∠C,∠B=∠D.
∴∠C=∠D.
∴OC=OD.
2.∵△ABC 是等边三角形,
∴∠ABC=∠ACB=60°.
∵OB,OC 是角平分线,
∴∠OBC=∠OCB=30°.
∵EE’和 FF’分别是OB,OC的垂直平分线,
∴EO=EB,FO=FC.
∴∠EBO=∠BOE=30°,∠FOC=∠FCO=30°.
∴∠OEF=∠OFE=60°.
∴△OEF 是等边三角形.
∴OE=EF=OF.
∴BE=EF=CF.
∴AB=3EF.
3.(1)∵AB=AC,AG⊥BC,∠BAC=120°,
∴∠BAD=1/2∠BAC=60°.
∵AB=AD,
∴△ABD 是等边三角形.
(2)证△EBD≌△FAD(ASA)进而得到 BE=AF.
