3.2.2双曲线的简单几何性质课件(共22张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 09:02:16 | ||
图片预览





文档简介
(共22张PPT)
第三章 圆锥曲线的方程
3.2.2 双曲线的简单几何性质
一、课题导入
定义
图象
方程
焦点
a,b,c 的关系
| |MF1|-|MF2| | =2a (0 < 2a<|F1F2|)
F1(-c, 0),F2(c, 0)
由方程定焦点:椭圆看大小, 双曲线看符号
F1(0,-c),F2(0,c)
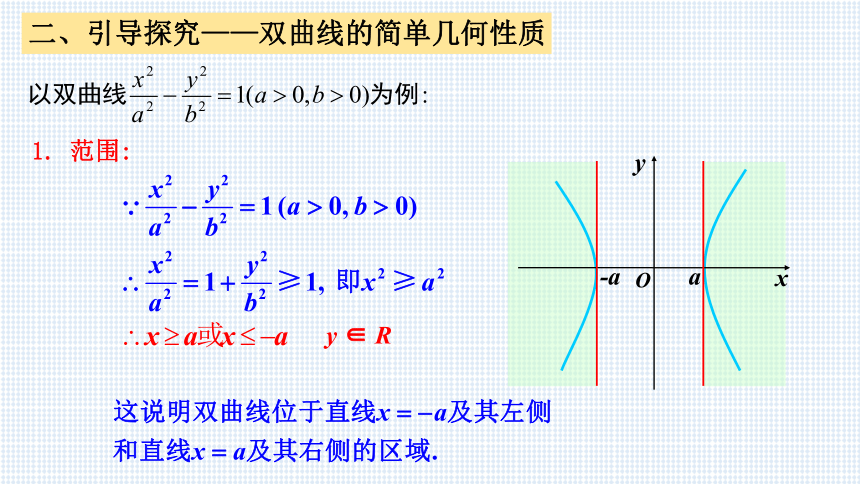
二、引导探究——双曲线的简单几何性质
x
y
-a
a
1. 范围:
O
y ∈ R
x
y
-a
a
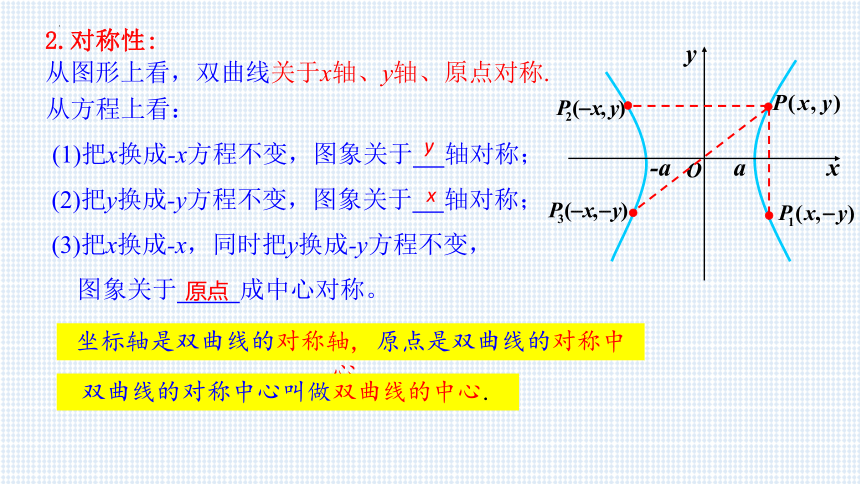
2.对称性:
O
从图形上看,双曲线关于x轴、y轴、原点对称.
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是双曲线的对称轴, 原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
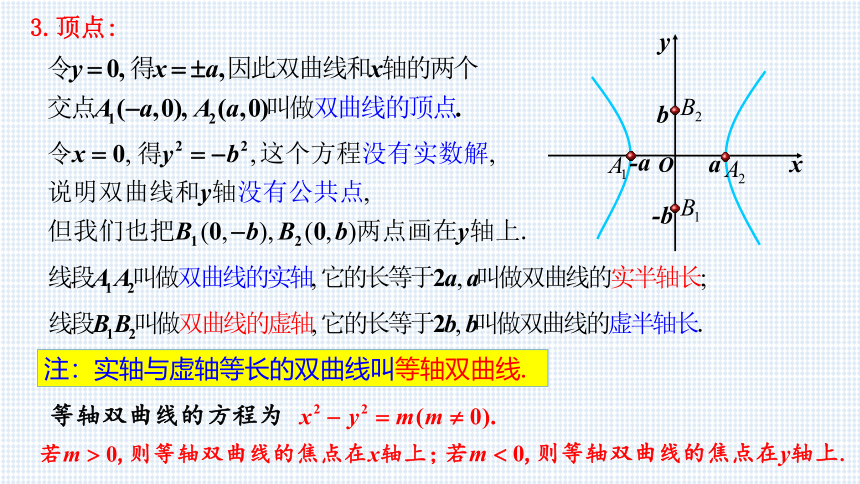
3.顶点:
x
y
O
-b
b
-a
a
注:实轴与虚轴等长的双曲线叫等轴双曲线.
4.渐近线:
双曲线 (a>0,b>0)与直线有什么样的位置关系?
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
4.双曲线的渐近线:
y
B2
A1
A2
B1
x
O
F2
F1
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,但永不相交.我们把这两条直线叫做双曲线的渐近线.
求法(适用于任意双曲线):
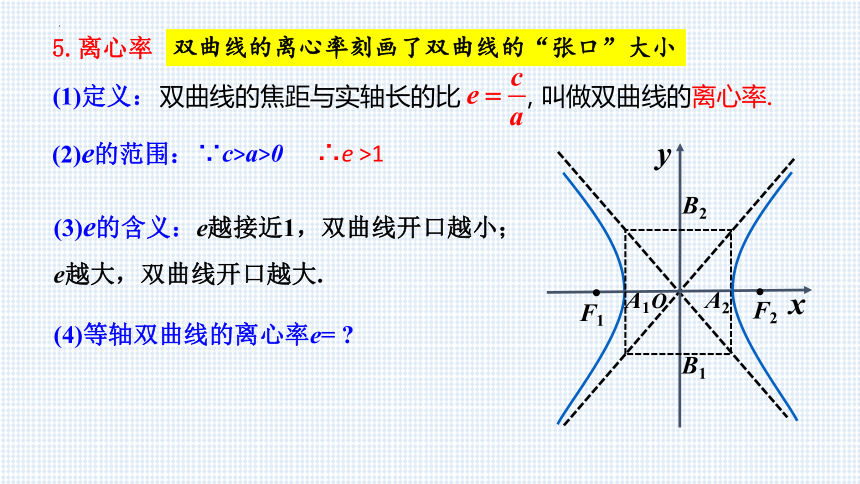
双曲线的离心率刻画了双曲线的“张口”大小
5.离心率
双曲线的焦距与实轴长的比 , 叫做双曲线的离心率.
∵c>a>0
∴e >1
(1)定义:
(2)e的范围:
(3)e的含义:e越接近1,双曲线开口越小;
e越大,双曲线开口越大.
(4)等轴双曲线的离心率e=
y
B2
A1
A2
B1
x
O
F2
F1
①等轴双曲线的方程:x2-y2=m (m≠0)
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
②等轴双曲线的渐近线:y=±x
(两条渐近线相互垂直)
③
方程
图形
范围
对称性
顶点
离心率
渐近线
关于x, y轴对称, 关于原点对称, 对称中心叫做双曲线的中心
A1(-a,0), A2(a,0)
线段A1A2叫实轴, 长度为2a
线段B1B2叫虚轴, 长度为2b
A1 (0,-a ), A2(0, a )
线段A1A2叫实轴 , 长度为2a
线段B1B2叫虚轴 , 长度为2b
双曲线的性质
三、典型例题1 由双曲线的标准方程研究其几何性质
可得实半轴长a=4,虚半轴长b=3
解: 把原方程化为标准方程
三、典型例题2 由双曲线的几何性质确定标准方程
方法总结
结论:双曲线的焦点到渐近线的距离恒等于b.
x
y
O
F1
F2
三、典型例题3 求离心率
D
三、典型例题4 轨迹问题
圆锥曲线的统一定义
三、典型例题5 与双曲线有关的弦长问题
四、课堂小结
第三章 圆锥曲线的方程
3.2.2 双曲线的简单几何性质
一、课题导入
定义
图象
方程
焦点
a,b,c 的关系
| |MF1|-|MF2| | =2a (0 < 2a<|F1F2|)
F1(-c, 0),F2(c, 0)
由方程定焦点:椭圆看大小, 双曲线看符号
F1(0,-c),F2(0,c)
二、引导探究——双曲线的简单几何性质
x
y
-a
a
1. 范围:
O
y ∈ R
x
y
-a
a
2.对称性:
O
从图形上看,双曲线关于x轴、y轴、原点对称.
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是双曲线的对称轴, 原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
3.顶点:
x
y
O
-b
b
-a
a
注:实轴与虚轴等长的双曲线叫等轴双曲线.
4.渐近线:
双曲线 (a>0,b>0)与直线有什么样的位置关系?
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
4.双曲线的渐近线:
y
B2
A1
A2
B1
x
O
F2
F1
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,但永不相交.我们把这两条直线叫做双曲线的渐近线.
求法(适用于任意双曲线):
双曲线的离心率刻画了双曲线的“张口”大小
5.离心率
双曲线的焦距与实轴长的比 , 叫做双曲线的离心率.
∵c>a>0
∴e >1
(1)定义:
(2)e的范围:
(3)e的含义:e越接近1,双曲线开口越小;
e越大,双曲线开口越大.
(4)等轴双曲线的离心率e=
y
B2
A1
A2
B1
x
O
F2
F1
①等轴双曲线的方程:x2-y2=m (m≠0)
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
②等轴双曲线的渐近线:y=±x
(两条渐近线相互垂直)
③
方程
图形
范围
对称性
顶点
离心率
渐近线
关于x, y轴对称, 关于原点对称, 对称中心叫做双曲线的中心
A1(-a,0), A2(a,0)
线段A1A2叫实轴, 长度为2a
线段B1B2叫虚轴, 长度为2b
A1 (0,-a ), A2(0, a )
线段A1A2叫实轴 , 长度为2a
线段B1B2叫虚轴 , 长度为2b
双曲线的性质
三、典型例题1 由双曲线的标准方程研究其几何性质
可得实半轴长a=4,虚半轴长b=3
解: 把原方程化为标准方程
三、典型例题2 由双曲线的几何性质确定标准方程
方法总结
结论:双曲线的焦点到渐近线的距离恒等于b.
x
y
O
F1
F2
三、典型例题3 求离心率
D
三、典型例题4 轨迹问题
圆锥曲线的统一定义
三、典型例题5 与双曲线有关的弦长问题
四、课堂小结
