3.2.1双曲线及其标准方程课件(共21张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 09:03:42 | ||
图片预览






文档简介
(共21张PPT)
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
一、课题导入
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 椭圆的标准方程
焦点在y轴
焦点在x轴
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
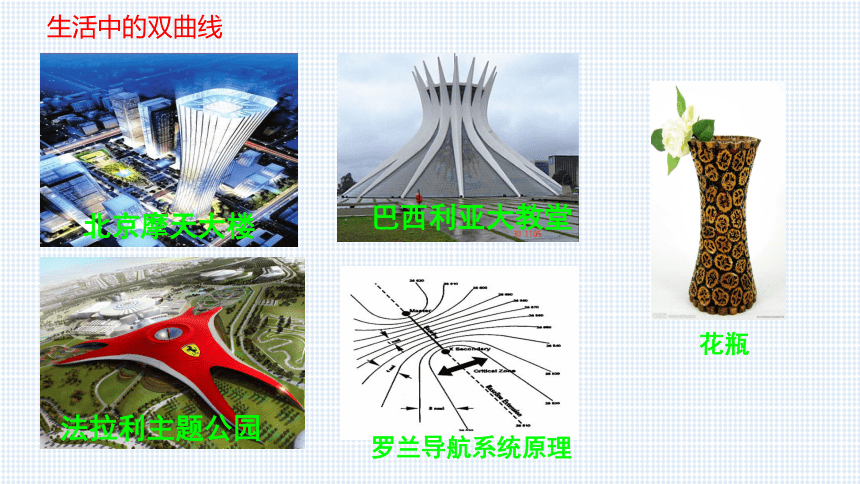
巴西利亚大教堂
北京摩天大楼
法拉利主题公园
花瓶
罗兰导航系统原理
生活中的双曲线
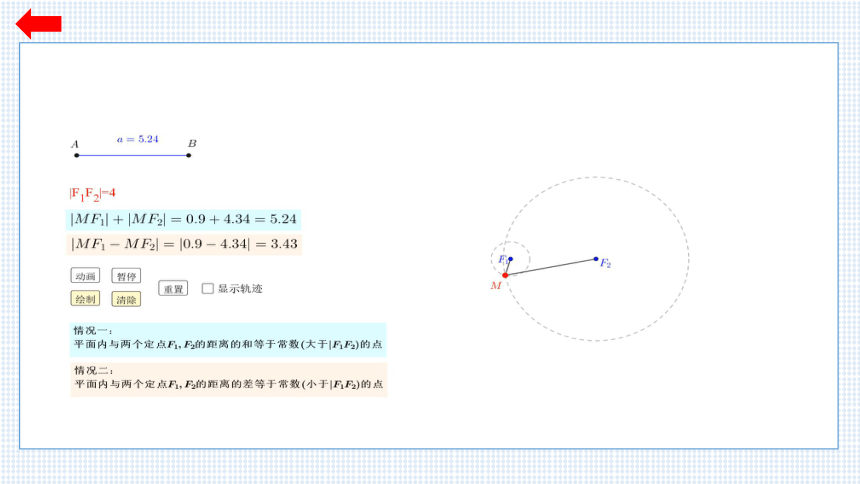
二、引导探究1——双曲线的定义
问题 如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
思考: 1.动点运动的轨迹是什么?
2.在运动过程中哪些量是变化的量? 哪些量是不变量?
3. 常数与|F1F2|的关系是什么?
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
数学符号刻画:
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
2
F
F
1
M
1.双曲线的定义
① 两个定点F1,F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
||MF1| - |MF2||=常数=2a(小于|F1F2|)
二、引导探究1——双曲线的定义
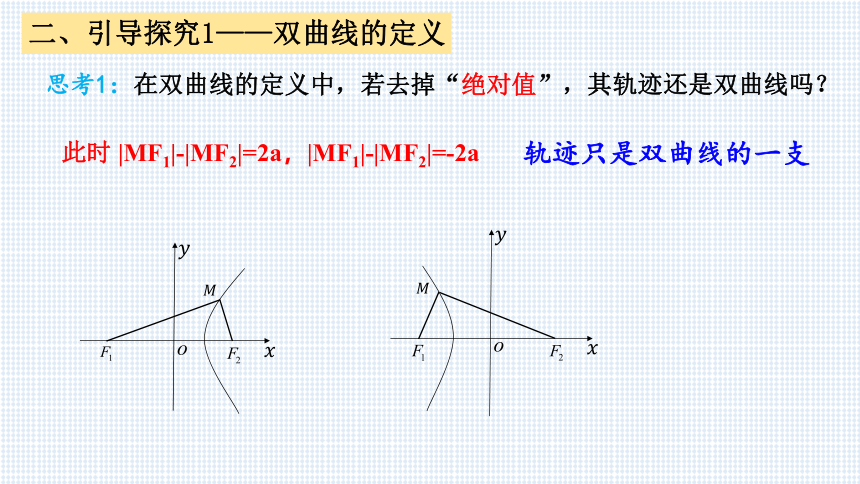
轨迹只是双曲线的一支
思考1:在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
o
此时 |MF1|-|MF2|=2a,|MF1|-|MF2|=-2a
o
二、引导探究1——双曲线的定义
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2:定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
F1
F2
M
F1
F2
M
二、引导探究1——双曲线的定义
二、引导探究2——双曲线的标准方程
1.建系设点:
2.找动点满足的条件:
3.几何条件代数化:
4.化简整理
x
F2
F1
M
(P119,类比椭圆方程的推导)
焦点在x轴上
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
焦点在x轴上
焦点在y轴上
二、引导探究2——双曲线的标准方程
①分母是a2和b2, 但a、b大小关系不定(a>b, a(1)焦点在x轴上:
(2)焦点在y轴上:
②c2=a2+b2(c最大:c>a>0,c>b>0)
③哪个系数为正,焦点就在哪个轴上,a就跟谁.
④焦点位置未知(或过两点),可设为mx2+ny2=1(mn<0).
2.双曲线的标准方程
F2
F1
M
x
O
y
O
M
F2
F1
x
y
二、引导探究2——双曲线的标准方程
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a|MF1|+|MF2|=2a (a>c)
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
由方程定焦点:椭圆看大小, 双曲线看符号
总结:
牛刀小试.根据方程,写出焦点坐标及a,b的值:
三、典型例题1 求双曲线的标准方程
例1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程.
三、典型例题1 求双曲线的标准方程
例2 求适合下列条件的双曲线的标准方程
(1)焦点在x轴上,a=4,b=3
(2)焦点在x轴上,经过点
(3)焦点为(0,-6),(0,6),且经过点(2,-5)
类型一:已知双曲线上两个点的坐标,求双曲线方程
待定系数法:设双曲线方程为mx2+ny2=1 (mn<0)
类型二:已知双曲线的焦点坐标及双曲线上一个点M的坐
标,求双曲线方程
定义法:由 ||MF1|-|MF2||=2a 计算a的值
方法总结
三、典型例题2 双曲线标准方程的应用
方法总结
三、典型例题3 双曲线的定义的应用
∴爆炸点P的轨迹是以A, B为焦点的双曲线靠近点B的一支.
解:如图示建立直角坐标系xOy, 使A, B两点在x轴上, 并且点O与线段AB的中点重合,
设爆炸点为P, 则
∴炮弹爆炸点的轨迹方程为
x
y
o
B
A
P
椭圆 双曲线
定 义
标准 方程 (焦点位置)
区别
a,b,c的关系 a2=b2+c2(a最大) c2=a2+b2(c最大)
一般形式
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
>|F1F2|
<|F1F2|
x轴:
y轴:
x轴:
y轴:
分母大小定焦点位置
以大小定a,b(a大b小)
系数正负定焦点位置
以正负定a,b(a正b负)
四、课堂小结
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
一、课题导入
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 椭圆的标准方程
焦点在y轴
焦点在x轴
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
巴西利亚大教堂
北京摩天大楼
法拉利主题公园
花瓶
罗兰导航系统原理
生活中的双曲线
二、引导探究1——双曲线的定义
问题 如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
思考: 1.动点运动的轨迹是什么?
2.在运动过程中哪些量是变化的量? 哪些量是不变量?
3. 常数与|F1F2|的关系是什么?
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
数学符号刻画:
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
2
F
F
1
M
1.双曲线的定义
① 两个定点F1,F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
||MF1| - |MF2||=常数=2a(小于|F1F2|)
二、引导探究1——双曲线的定义
轨迹只是双曲线的一支
思考1:在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
o
此时 |MF1|-|MF2|=2a,|MF1|-|MF2|=-2a
o
二、引导探究1——双曲线的定义
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2:定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
F1
F2
M
F1
F2
M
二、引导探究1——双曲线的定义
二、引导探究2——双曲线的标准方程
1.建系设点:
2.找动点满足的条件:
3.几何条件代数化:
4.化简整理
x
F2
F1
M
(P119,类比椭圆方程的推导)
焦点在x轴上
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
焦点在x轴上
焦点在y轴上
二、引导探究2——双曲线的标准方程
①分母是a2和b2, 但a、b大小关系不定(a>b, a
(2)焦点在y轴上:
②c2=a2+b2(c最大:c>a>0,c>b>0)
③哪个系数为正,焦点就在哪个轴上,a就跟谁.
④焦点位置未知(或过两点),可设为mx2+ny2=1(mn<0).
2.双曲线的标准方程
F2
F1
M
x
O
y
O
M
F2
F1
x
y
二、引导探究2——双曲线的标准方程
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
由方程定焦点:椭圆看大小, 双曲线看符号
总结:
牛刀小试.根据方程,写出焦点坐标及a,b的值:
三、典型例题1 求双曲线的标准方程
例1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程.
三、典型例题1 求双曲线的标准方程
例2 求适合下列条件的双曲线的标准方程
(1)焦点在x轴上,a=4,b=3
(2)焦点在x轴上,经过点
(3)焦点为(0,-6),(0,6),且经过点(2,-5)
类型一:已知双曲线上两个点的坐标,求双曲线方程
待定系数法:设双曲线方程为mx2+ny2=1 (mn<0)
类型二:已知双曲线的焦点坐标及双曲线上一个点M的坐
标,求双曲线方程
定义法:由 ||MF1|-|MF2||=2a 计算a的值
方法总结
三、典型例题2 双曲线标准方程的应用
方法总结
三、典型例题3 双曲线的定义的应用
∴爆炸点P的轨迹是以A, B为焦点的双曲线靠近点B的一支.
解:如图示建立直角坐标系xOy, 使A, B两点在x轴上, 并且点O与线段AB的中点重合,
设爆炸点为P, 则
∴炮弹爆炸点的轨迹方程为
x
y
o
B
A
P
椭圆 双曲线
定 义
标准 方程 (焦点位置)
区别
a,b,c的关系 a2=b2+c2(a最大) c2=a2+b2(c最大)
一般形式
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
>|F1F2|
<|F1F2|
x轴:
y轴:
x轴:
y轴:
分母大小定焦点位置
以大小定a,b(a大b小)
系数正负定焦点位置
以正负定a,b(a正b负)
四、课堂小结
