12.2 第3课时 “角边角”“角角边” 教学设计(表格式) 人教版数学八年级上册
文档属性
| 名称 | 12.2 第3课时 “角边角”“角角边” 教学设计(表格式) 人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 138.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 00:00:00 | ||
图片预览

文档简介
教育教学研究室电子集体备课教案
备课日期: 2023 年 月 日
课题 12.2 全等三角形的判定 授课日期
教学内容 第3课时 “角边角”“角角边” 课 时 1课时
教 学 目 标 1.探索三角形全等的“ASA”和“AAS”的条件. 2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等. 3.“角边角”和“角角边”判定方法的探究以及适合“角边角”判定方法的条件的寻找.(难点)
本课在教材中的地位、作用 本节课学生进一步提高合情推理能力和感受转化的思想,为今后研究几何问题建立一定的模式。
教学重点 探索三角形全等的“ASA”和“AAS”的条件.
教学难点 会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
教法学法 讲授法、合作探究法
教具学具准备 多媒体课件、三角尺
学科思政
新授课基本流程:预学导学、互助探究、分层提高、总结归纳、巩固反馈
教学环节 教师活动 学生活动 设计意图 个性化调整
预学导学 一、知识链接 1.能够 的两个三角形叫做全等三角形. 2.判定两个三角形全等方法有哪些?
边边边: 分别相等的两个三角形全等. 边角边: 和它们的 分别相等的两个三角形全等.
新课导入 (
3
2
1
)如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适 你能说明其中的理由吗
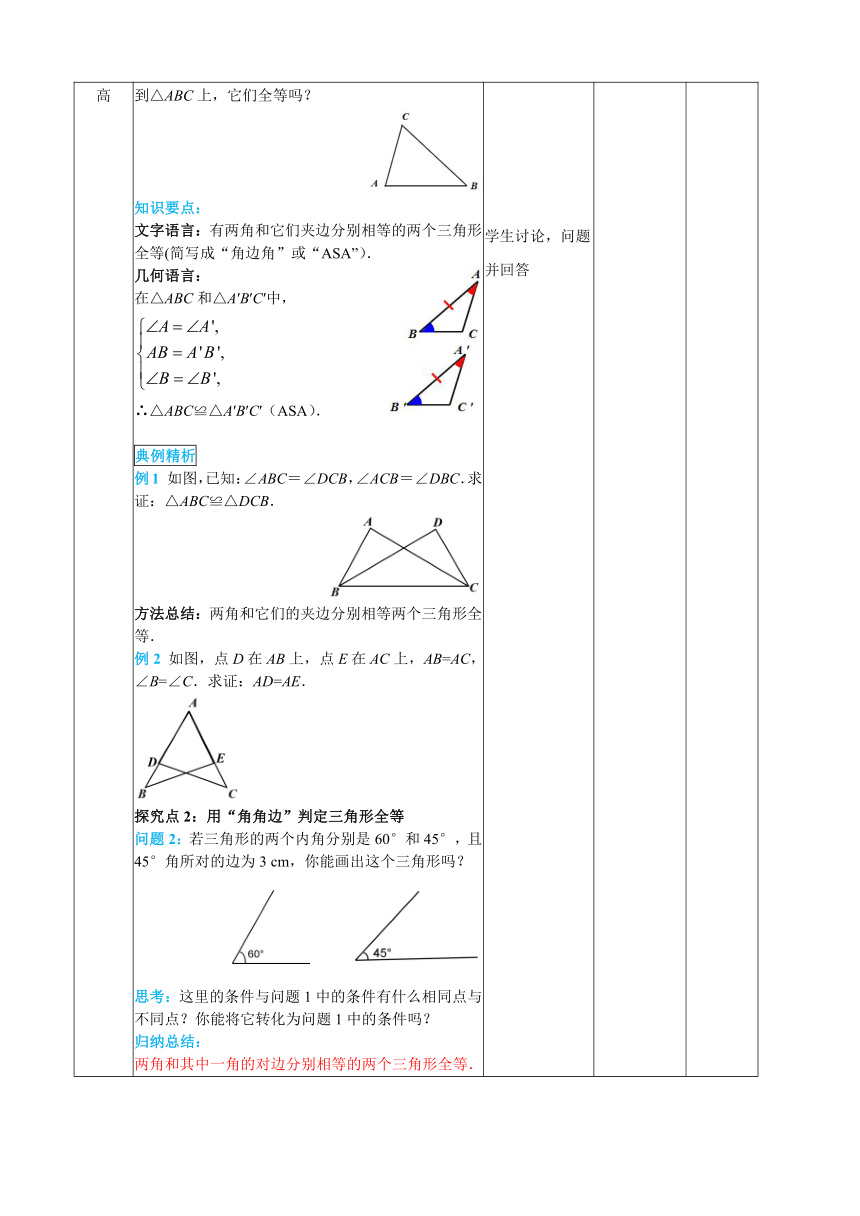
互助探究 分层提高 要点探究 探究点1:三角形全等的判定(“角边角”) 问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢? 作图探究:先任意画出一个△ABC,再画一个△A′B′C′, 使A′B′=AB,∠A′=∠A,∠B′=∠B (即使两角和它们的夹边分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗? 知识要点: 文字语言:有两角和它们夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”). 几何语言: 在△ABC和△A′B′C′中, ∴△ABC≌△A′B′C′(ASA). 典例精析 例1 如图,已知:∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB. 方法总结:两角和它们的夹边分别相等两个三角形全等. 例2 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE. 探究点2:用“角角边”判定三角形全等 问题2:若三角形的两个内角分别是60°和45°,且45°角所对的边为3 cm,你能画出这个三角形吗? 思考:这里的条件与问题1中的条件有什么相同点与不同点?你能将它转化为问题1中的条件吗? 归纳总结: 两角和其中一角的对边分别相等的两个三角形全等. 简写成“角角边”或“AAS”. 在△ABC和△A′B′C′中, ∴△ABC≌△A′B′C′(AAS). 典例精析 例3:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF. 例4:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m,CE⊥m,垂足分别为点D、E.求证: △BDA≌△AEC; (2)DE=BD+CE. 方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化. 学生思考问题并回答 学生讨论,问题并回答
总结归纳
巩固反馈 1.△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列补充的条件中错误的是( ) A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F 2.在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°, 且AC=A′C′,那么这两个三角形( ) A.一定不全等 B.一定全等 C.不一定全等 D.以上都不对
3.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断下面的两个三角形是否全等,并说明理由. 4.如图,∠ACB=∠DFE,BC=EF,那么应补充一个条件: ,才能使△ABC≌△DEF(写出一个即可). 学生独立完成,
课后作业 布置 必做题 课本第43页第4、5、6题 完成 总时间 分钟
选做题 课本第44页第11题 完成 总时间 分钟
实践题
板书设计 12.2.3“角边角”“角角边” 1.角边角:两角及其夹边分别相等的两个三角形全等.简记为“角边角”或“ASA”. 2.角角边:两角分别相等且其中一组等角的对边相等的两个三角形全等.简记为“角角边”或“AAS”. 3.三角形全等是证明线段相等或角相等的常用方法.
教学反思
组长签字 教研组长签字 教科室签字
备课日期: 2023 年 月 日
课题 12.2 全等三角形的判定 授课日期
教学内容 第3课时 “角边角”“角角边” 课 时 1课时
教 学 目 标 1.探索三角形全等的“ASA”和“AAS”的条件. 2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等. 3.“角边角”和“角角边”判定方法的探究以及适合“角边角”判定方法的条件的寻找.(难点)
本课在教材中的地位、作用 本节课学生进一步提高合情推理能力和感受转化的思想,为今后研究几何问题建立一定的模式。
教学重点 探索三角形全等的“ASA”和“AAS”的条件.
教学难点 会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
教法学法 讲授法、合作探究法
教具学具准备 多媒体课件、三角尺
学科思政
新授课基本流程:预学导学、互助探究、分层提高、总结归纳、巩固反馈
教学环节 教师活动 学生活动 设计意图 个性化调整
预学导学 一、知识链接 1.能够 的两个三角形叫做全等三角形. 2.判定两个三角形全等方法有哪些?
边边边: 分别相等的两个三角形全等. 边角边: 和它们的 分别相等的两个三角形全等.
新课导入 (
3
2
1
)如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适 你能说明其中的理由吗
互助探究 分层提高 要点探究 探究点1:三角形全等的判定(“角边角”) 问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢? 作图探究:先任意画出一个△ABC,再画一个△A′B′C′, 使A′B′=AB,∠A′=∠A,∠B′=∠B (即使两角和它们的夹边分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗? 知识要点: 文字语言:有两角和它们夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”). 几何语言: 在△ABC和△A′B′C′中, ∴△ABC≌△A′B′C′(ASA). 典例精析 例1 如图,已知:∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB. 方法总结:两角和它们的夹边分别相等两个三角形全等. 例2 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE. 探究点2:用“角角边”判定三角形全等 问题2:若三角形的两个内角分别是60°和45°,且45°角所对的边为3 cm,你能画出这个三角形吗? 思考:这里的条件与问题1中的条件有什么相同点与不同点?你能将它转化为问题1中的条件吗? 归纳总结: 两角和其中一角的对边分别相等的两个三角形全等. 简写成“角角边”或“AAS”. 在△ABC和△A′B′C′中, ∴△ABC≌△A′B′C′(AAS). 典例精析 例3:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF. 例4:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m,CE⊥m,垂足分别为点D、E.求证: △BDA≌△AEC; (2)DE=BD+CE. 方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化. 学生思考问题并回答 学生讨论,问题并回答
总结归纳
巩固反馈 1.△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列补充的条件中错误的是( ) A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F 2.在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°, 且AC=A′C′,那么这两个三角形( ) A.一定不全等 B.一定全等 C.不一定全等 D.以上都不对
3.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断下面的两个三角形是否全等,并说明理由. 4.如图,∠ACB=∠DFE,BC=EF,那么应补充一个条件: ,才能使△ABC≌△DEF(写出一个即可). 学生独立完成,
课后作业 布置 必做题 课本第43页第4、5、6题 完成 总时间 分钟
选做题 课本第44页第11题 完成 总时间 分钟
实践题
板书设计 12.2.3“角边角”“角角边” 1.角边角:两角及其夹边分别相等的两个三角形全等.简记为“角边角”或“ASA”. 2.角角边:两角分别相等且其中一组等角的对边相等的两个三角形全等.简记为“角角边”或“AAS”. 3.三角形全等是证明线段相等或角相等的常用方法.
教学反思
组长签字 教研组长签字 教科室签字
