22.3实际问题与二次函数强化训练(含答案) 人教版数学九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数强化训练(含答案) 人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 565.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 18:22:34 | ||
图片预览



文档简介
22.3实际问题与二次函数
一、单选题
1.用一根长为12 cm的细铁丝围成一个矩形,则围成的矩形面积最大为( )
A.7 cm2 B.8 cm2 C.9 cm2 D.10 cm2
2.某种商品每天的销售利润y(元)与单价x(元)之间的函数关系式为.则这种商品每天的最大利润为( )
A.0.1元 B.3元 C.25元 D.75元
3.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是;②小球运动的时间为;③小球抛出3秒时,速度为0;
④当时,小球的高度.其中正确的是( )
A.①④ B.①② C.②③④ D.②④
4.如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
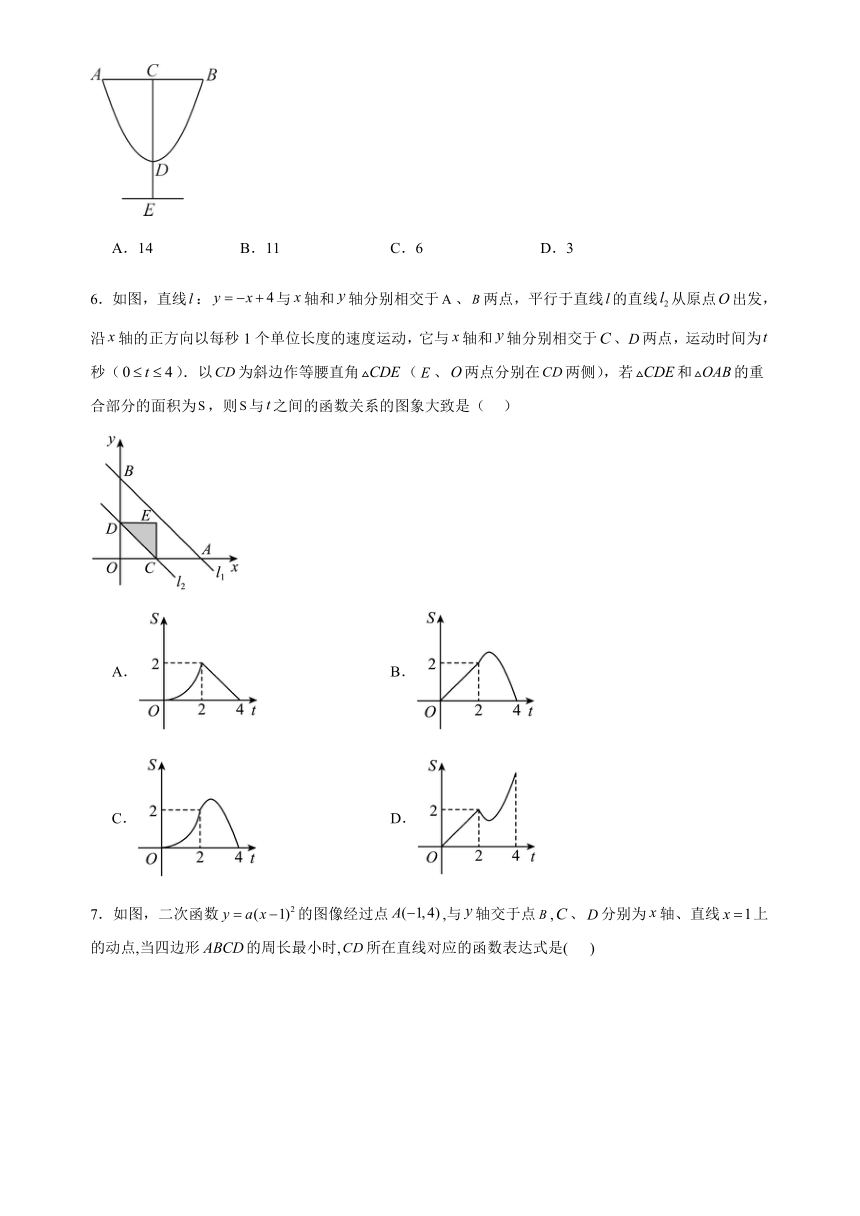
5.小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
6.如图,直线:与轴和轴分别相交于、两点,平行于直线的直线从原点出发,沿轴的正方向以每秒1个单位长度的速度运动,它与轴和轴分别相交于、两点,运动时间为秒().以为斜边作等腰直角(、两点分别在两侧),若和的重合部分的面积为,则与之间的函数关系的图象大致是( )
A. B.
C. D.
7.如图,二次函数的图像经过点,与轴交于点,、分别为轴、直线上的动点,当四边形的周长最小时,所在直线对应的函数表达式是( )
A. B. C. D.
8.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
9.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形阴影部分片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为
A., B., C., D.,
10.在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为A,第二次从落地点A反弹后继续向前飞行,落地点为B,如图,已知第一次飞行经过t(秒)时球距离地面的高度h(米)适用公式,足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )
A. B.
C. D.
二、填空题
11.二次函数y=x2﹣2x﹣3与x轴两交点之间的距离为 .抛物线顶点、与x轴正半轴和y轴的交点围成的三角形面积是 .
12.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
13.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为时,水面的宽度为 .
14.如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,运动时间t= 秒时四边形EFGH的面积最小.
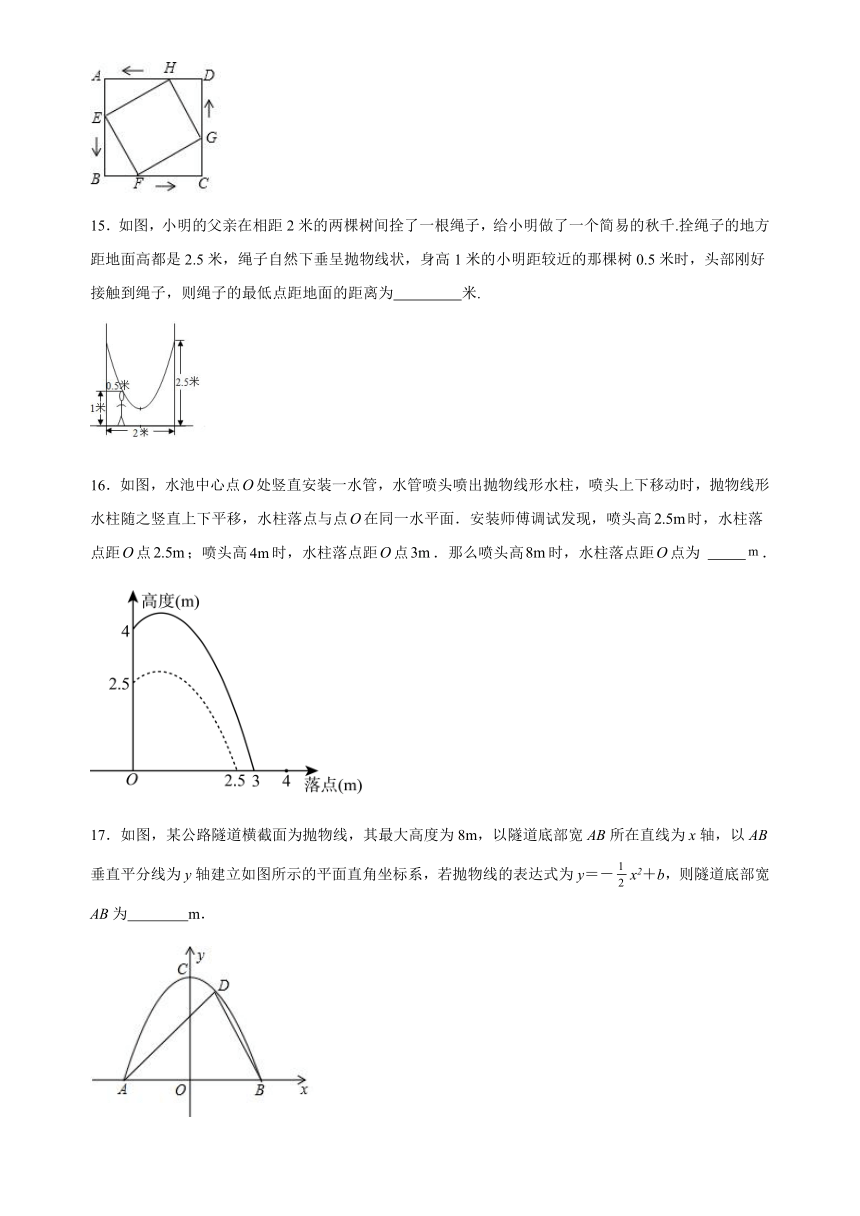
15.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
16.如图,水池中心点处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点在同一水平面.安装师傅调试发现,喷头高时,水柱落点距点;喷头高时,水柱落点距点.那么喷头高时,水柱落点距点为 .
17.如图,某公路隧道横截面为抛物线,其最大高度为8m,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,若抛物线的表达式为y=-x2+b,则隧道底部宽AB为 m.
三、解答题
18.我校各班积极参与班级文化墙建设,某广告公司准备为年级设计一幅周长为12m的矩形广告牌,表彰年级优秀学生,广告设计费为每平方米400元,设矩形一边长为x(m),面积为S(m2).
(1)求S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为获得最多的广告设计费,广告牌的长,宽各应多少米? 广告设计费最多是多少?
19.如图1,要利用一面墙(墙长为)建羊圈,用的围栏围成两个大小相同的矩形羊圈,设羊圈的一边长为,羊圈总面积为.
(1)请问能否围成总面积为的羊圈,若能,请求出的长;若不能,请说明理由.
(2)如果两个矩形羊圈各开一个宽的门(如图2),在不浪费围栏的情况下,求y与x的函数关系式并写出x的取值范围,求出羊圈总面积最大值.
20.某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量(件)与销售时间(天)之间的关系式是 ,销售单价(元/件)与销售时间(天)之间的函数关系如图所示.
(1)第15天的日销售量为_________件;
(2)当时,求日销售额的最大值;
(3)在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?
21.如图1,劳动课同学们利用喷水头喷出的水对草坪进行喷灌作业以养护草坪.如图2,点O处有一个喷水头,距离喷水头的M处有一棵高度是的树,距离这棵树的N处有一面高的围墙.建立如图所示平面直角坐标系.已知喷水头喷出的水柱的竖直高度与水平距离近似满足函数关系.
(1)某次喷水浇灌时,测得x与y的几组数据如下:
0 2 6 10 12
0
①根据上述数据,求满足的函数关系;
②求喷水头喷出的水柱最大高度;
又一次喷水浇灌时,已知喷水头喷出的水柱的竖直高度y与水平距离x近似满足函数关系.假设喷水头喷出的水柱能够越过这棵树,且不会浇到墙外,求出同时满足这两个要求的常数b的范围_________.
参考答案:
1.C
2.C
3.C
4.B
5.B
6.C
7.D
8.C
9.D
10.B
11. 4 3
12.
13.16
14.3.
15.0.5
16.4
17.8
18.(1)s=-x2+6x(019.(1)不能围成总面积为的羊圈,理由见解析
(2)羊圈总面积最大值
20.(1)30
(2)2100元
(3)9天
21.(1)①;②
(2)
一、单选题
1.用一根长为12 cm的细铁丝围成一个矩形,则围成的矩形面积最大为( )
A.7 cm2 B.8 cm2 C.9 cm2 D.10 cm2
2.某种商品每天的销售利润y(元)与单价x(元)之间的函数关系式为.则这种商品每天的最大利润为( )
A.0.1元 B.3元 C.25元 D.75元
3.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是;②小球运动的时间为;③小球抛出3秒时,速度为0;
④当时,小球的高度.其中正确的是( )
A.①④ B.①② C.②③④ D.②④
4.如图,在矩形ABCD中,AB=a,BC=b,≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A. B. C. D.
5.小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
6.如图,直线:与轴和轴分别相交于、两点,平行于直线的直线从原点出发,沿轴的正方向以每秒1个单位长度的速度运动,它与轴和轴分别相交于、两点,运动时间为秒().以为斜边作等腰直角(、两点分别在两侧),若和的重合部分的面积为,则与之间的函数关系的图象大致是( )
A. B.
C. D.
7.如图,二次函数的图像经过点,与轴交于点,、分别为轴、直线上的动点,当四边形的周长最小时,所在直线对应的函数表达式是( )
A. B. C. D.
8.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
9.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形阴影部分片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为
A., B., C., D.,
10.在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为A,第二次从落地点A反弹后继续向前飞行,落地点为B,如图,已知第一次飞行经过t(秒)时球距离地面的高度h(米)适用公式,足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )
A. B.
C. D.
二、填空题
11.二次函数y=x2﹣2x﹣3与x轴两交点之间的距离为 .抛物线顶点、与x轴正半轴和y轴的交点围成的三角形面积是 .
12.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
13.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为时,水面的宽度为 .
14.如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,运动时间t= 秒时四边形EFGH的面积最小.
15.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
16.如图,水池中心点处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点在同一水平面.安装师傅调试发现,喷头高时,水柱落点距点;喷头高时,水柱落点距点.那么喷头高时,水柱落点距点为 .
17.如图,某公路隧道横截面为抛物线,其最大高度为8m,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,若抛物线的表达式为y=-x2+b,则隧道底部宽AB为 m.
三、解答题
18.我校各班积极参与班级文化墙建设,某广告公司准备为年级设计一幅周长为12m的矩形广告牌,表彰年级优秀学生,广告设计费为每平方米400元,设矩形一边长为x(m),面积为S(m2).
(1)求S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为获得最多的广告设计费,广告牌的长,宽各应多少米? 广告设计费最多是多少?
19.如图1,要利用一面墙(墙长为)建羊圈,用的围栏围成两个大小相同的矩形羊圈,设羊圈的一边长为,羊圈总面积为.
(1)请问能否围成总面积为的羊圈,若能,请求出的长;若不能,请说明理由.
(2)如果两个矩形羊圈各开一个宽的门(如图2),在不浪费围栏的情况下,求y与x的函数关系式并写出x的取值范围,求出羊圈总面积最大值.
20.某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量(件)与销售时间(天)之间的关系式是 ,销售单价(元/件)与销售时间(天)之间的函数关系如图所示.
(1)第15天的日销售量为_________件;
(2)当时,求日销售额的最大值;
(3)在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?
21.如图1,劳动课同学们利用喷水头喷出的水对草坪进行喷灌作业以养护草坪.如图2,点O处有一个喷水头,距离喷水头的M处有一棵高度是的树,距离这棵树的N处有一面高的围墙.建立如图所示平面直角坐标系.已知喷水头喷出的水柱的竖直高度与水平距离近似满足函数关系.
(1)某次喷水浇灌时,测得x与y的几组数据如下:
0 2 6 10 12
0
①根据上述数据,求满足的函数关系;
②求喷水头喷出的水柱最大高度;
又一次喷水浇灌时,已知喷水头喷出的水柱的竖直高度y与水平距离x近似满足函数关系.假设喷水头喷出的水柱能够越过这棵树,且不会浇到墙外,求出同时满足这两个要求的常数b的范围_________.
参考答案:
1.C
2.C
3.C
4.B
5.B
6.C
7.D
8.C
9.D
10.B
11. 4 3
12.
13.16
14.3.
15.0.5
16.4
17.8
18.(1)s=-x2+6x(0
(2)羊圈总面积最大值
20.(1)30
(2)2100元
(3)9天
21.(1)①;②
(2)
同课章节目录
