12.2全等三角形的判定1 教学设计(表格式) 人教版数学八年级上册
文档属性
| 名称 | 12.2全等三角形的判定1 教学设计(表格式) 人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 00:00:00 | ||
图片预览

文档简介
备课日期: 2023 年 月 日
课题 12.1 全等三角形 授课日期
教学内容 12.1.2 三角形的判定1(边边边) 课 4时 1课时
教 学 目 标 了解三角形的稳定性,会应用“边边边”判定两个三角形全等。 经历探索“边边边”判定全等三角形的过程,体会利用操作、归纳获得数学结论的过程.
本课在教材中的地位、作用 对于全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第-步。它是两三角形间最简单、最常见的关系。本节《探索三角形全等的条件》是学生在认识三角形的基础上,在了解全等图形和全等三角形以后进行学习的,它既是前面所学知识的延伸与拓展,又是后继学习探索相似形的条件的基础,并且是用以说明线段相等、两角相等的重要依据。因此,本节课的知识具有承上启下的作用。
教学重点 三角形全等条件的探索过程.
教学难点 指导学生分析问题,寻找判定三角形全等的条件.
教法学法 探究法,合作交流。
教具学具准备 Ppt 三角形
学科思政 通过三角形彩旗,穿插国庆节的来历,对学生进行爱国主义教育。
新授课基本流程:预学导学、互助探究、分层提高、总结归纳、巩固反馈
教学环节 教师活动 学生活动 设计意图 个性化调整
预学导学 为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗? 在教师引导下回忆前面知识,为探究新知识作好准备 问题的提出使学生产生浓厚的兴趣,激发他们的探究欲望 学生模仿上面的研究方法,在教师的引导下完成操作过程,通过交流,归纳得出结论,同时也明确判定三角形全等需要三个条件.
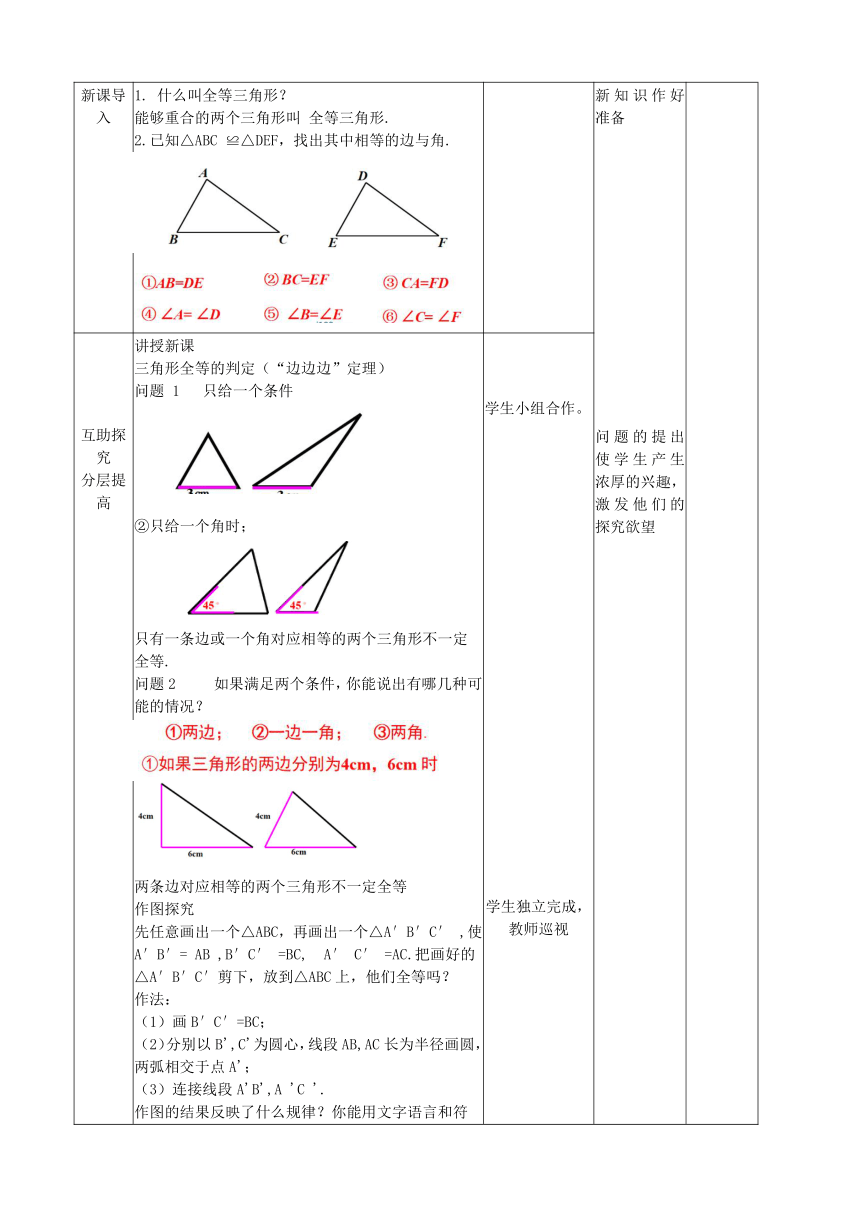
新课导入 1. 什么叫全等三角形? 能够重合的两个三角形叫 全等三角形. 2.已知△ABC ≌△DEF,找出其中相等的边与角.
互助探究 分层提高 讲授新课 三角形全等的判定(“边边边”定理) 问题 1 只给一个条件 ②只给一个角时; 只有一条边或一个角对应相等的两个三角形不一定全等. 问题2 如果满足两个条件,你能说出有哪几种可能的情况? 两条边对应相等的两个三角形不一定全等 作图探究 先任意画出一个△ABC,再画出一个△A′B′C′ ,使 A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗? 作法: (1)画B′C′=BC; (2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A'; (3)连接线段A'B',A 'C '. 作图的结果反映了什么规律?你能用文字语言和符号语言概括吗? “边边边”判定方法 文字语言:三边对应相等的两个三角形全等。 (简写为“边边边”或“SSS”) 几何语言: 例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD 证明的书写步骤: 用尺规作一个角等于已知角 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 作法: (1)以点O 为圆心,任意长为半径画弧,分别交OA, OB 于点C、D; (2)画一条射线O′A′,以点O′为圆心,OC 长为半 径画弧,交O′A′于点C′; (3)以点C′为圆心,CD 长为半径画弧,与第2 步中 所画的弧交于点D′; (4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 学生小组合作。 学生独立完成,教师巡视
总结归纳 有三边对应相等的两个三角形全等(简写成 “SSS”)
巩固反馈 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?请完成下列解题步骤. 学生独立完成,
2.如图,D、F是线段BC上的两点,AB=CE,AF=DE使 △ABF≌△ECD ,还需要条件 . 学生独立完成,
课后作业 布置 必做题 完成 总时间 15分钟
选做题 完成 总时间 10分钟
实践题 3.已知:如图 ,AC=FE,AD=FB,BC=DE. 求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
板书设计 三角形全等的判定 “边边边” 有三边对应相等的两个三角形全等(简写成 “SSS”)
教学反思
组长签字 教研组长签字 教科室签字
课题 12.1 全等三角形 授课日期
教学内容 12.1.2 三角形的判定1(边边边) 课 4时 1课时
教 学 目 标 了解三角形的稳定性,会应用“边边边”判定两个三角形全等。 经历探索“边边边”判定全等三角形的过程,体会利用操作、归纳获得数学结论的过程.
本课在教材中的地位、作用 对于全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第-步。它是两三角形间最简单、最常见的关系。本节《探索三角形全等的条件》是学生在认识三角形的基础上,在了解全等图形和全等三角形以后进行学习的,它既是前面所学知识的延伸与拓展,又是后继学习探索相似形的条件的基础,并且是用以说明线段相等、两角相等的重要依据。因此,本节课的知识具有承上启下的作用。
教学重点 三角形全等条件的探索过程.
教学难点 指导学生分析问题,寻找判定三角形全等的条件.
教法学法 探究法,合作交流。
教具学具准备 Ppt 三角形
学科思政 通过三角形彩旗,穿插国庆节的来历,对学生进行爱国主义教育。
新授课基本流程:预学导学、互助探究、分层提高、总结归纳、巩固反馈
教学环节 教师活动 学生活动 设计意图 个性化调整
预学导学 为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗? 在教师引导下回忆前面知识,为探究新知识作好准备 问题的提出使学生产生浓厚的兴趣,激发他们的探究欲望 学生模仿上面的研究方法,在教师的引导下完成操作过程,通过交流,归纳得出结论,同时也明确判定三角形全等需要三个条件.
新课导入 1. 什么叫全等三角形? 能够重合的两个三角形叫 全等三角形. 2.已知△ABC ≌△DEF,找出其中相等的边与角.
互助探究 分层提高 讲授新课 三角形全等的判定(“边边边”定理) 问题 1 只给一个条件 ②只给一个角时; 只有一条边或一个角对应相等的两个三角形不一定全等. 问题2 如果满足两个条件,你能说出有哪几种可能的情况? 两条边对应相等的两个三角形不一定全等 作图探究 先任意画出一个△ABC,再画出一个△A′B′C′ ,使 A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗? 作法: (1)画B′C′=BC; (2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A'; (3)连接线段A'B',A 'C '. 作图的结果反映了什么规律?你能用文字语言和符号语言概括吗? “边边边”判定方法 文字语言:三边对应相等的两个三角形全等。 (简写为“边边边”或“SSS”) 几何语言: 例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD 证明的书写步骤: 用尺规作一个角等于已知角 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 作法: (1)以点O 为圆心,任意长为半径画弧,分别交OA, OB 于点C、D; (2)画一条射线O′A′,以点O′为圆心,OC 长为半 径画弧,交O′A′于点C′; (3)以点C′为圆心,CD 长为半径画弧,与第2 步中 所画的弧交于点D′; (4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 学生小组合作。 学生独立完成,教师巡视
总结归纳 有三边对应相等的两个三角形全等(简写成 “SSS”)
巩固反馈 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?请完成下列解题步骤. 学生独立完成,
2.如图,D、F是线段BC上的两点,AB=CE,AF=DE使 △ABF≌△ECD ,还需要条件 . 学生独立完成,
课后作业 布置 必做题 完成 总时间 15分钟
选做题 完成 总时间 10分钟
实践题 3.已知:如图 ,AC=FE,AD=FB,BC=DE. 求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
板书设计 三角形全等的判定 “边边边” 有三边对应相等的两个三角形全等(简写成 “SSS”)
教学反思
组长签字 教研组长签字 教科室签字
