九年级数学上册课件(北师大版) 6.2.1 反比例函数的图象与性质(第1课时)(共20张PPT)
文档属性
| 名称 | 九年级数学上册课件(北师大版) 6.2.1 反比例函数的图象与性质(第1课时)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 863.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第六章 反比例函数
第2节 反比例函数的图象与性质(1)
学习目标
1.会用描点法画出反比例函数的图象,并掌握反比例函数图象的特征.(重点)
2.会利用反比例函数图象解决相关问题.(难点)
情景引入
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
3.还记得一次函数的图像与性质吗?
一般地,形如 ( k是常数, k ≠0 )的函数叫做反比例函数.
函数 正比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx(k是常数,k≠0)
直线(经过原点)
一、三象限
从左到右上升
y随x的增大而增大
二、四象限
从左到右下降
y随x的增大而减小
反比例函数
?
你还记得画函数图象的步骤吗?
① 列表;
②描点;
③连线。
反比例函数的图象
1—
问题:如何画反比例函数 的图象?
列表
描点
连线
解:列表如下
x -8 -4 -3 -2 -1 1 2 3 4 8
y
-1
-2
-4
-8
8
4
2
1
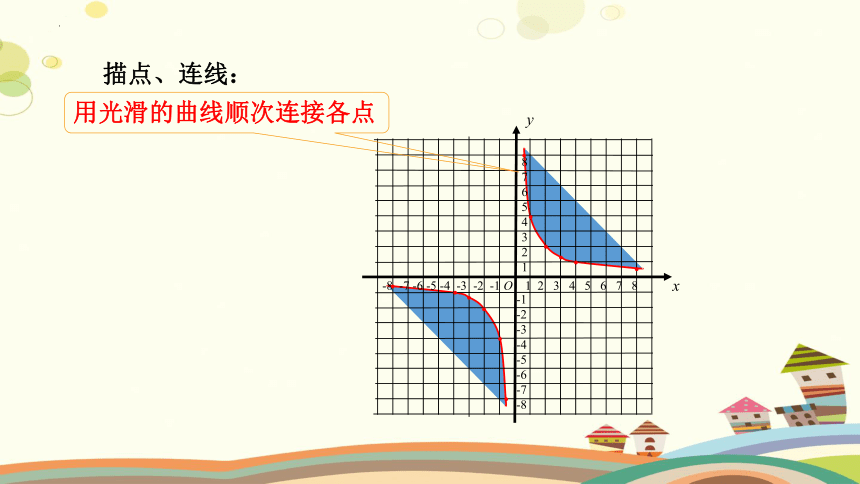
描点、连线:
x
-8 -7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8
y
-1
-2
-3
-4
-5
-6
-7
-8
87654321
用光滑的曲线顺次连接各点
想一想:你认为作反比例函数图象时应注意哪些问题
1.列表时,自变量的值可以选取一些互为相反数的值这样既可简化计算,又便于对称性描点;
2.列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
3.连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……
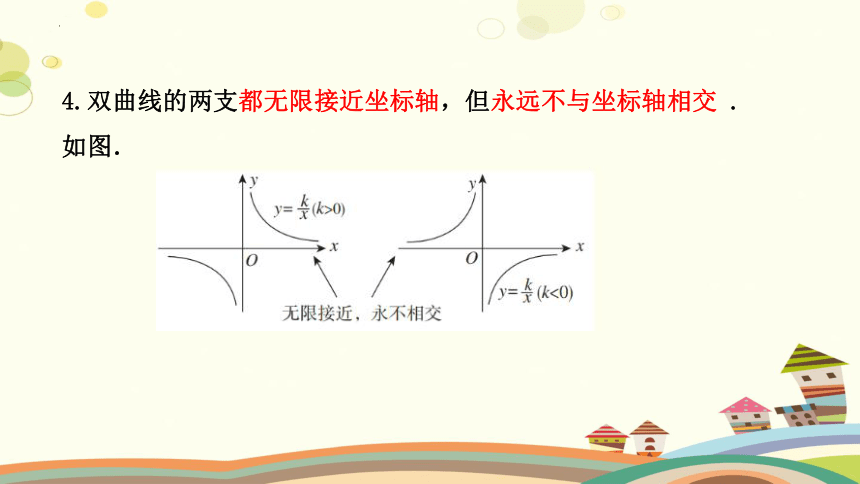
4.双曲线的两支都无限接近坐标轴,但永远不与坐标轴相交 .如图.
在图中的平面直角坐标系中画出反比例函数 的图象.
做一做
(1)观察 和 的图象,它们有什么相同点和不同点
(2)反比例函数 的图象在哪两个象限,由什么确定?
x
y
x
y
双曲线
轴对称图形,也是以原点为对称中心的中心对称图形.
O
O
议一议
相同点:1.两支曲线构成;
2.与坐标轴不相交;
3.图象自身关于原点成中心对称;
4.图象自身是轴对称图形.
不同点:的图象在第一、三象限;
的图象在第二、四象限.
形状: 反比例函数 的图象由两支曲线组成,因此称反比例函数 的图象为双曲线.
位置:由k决定:
当k>0时,两支曲线分别位于______________内;
当k<0时,两支曲线分别位于______________内.
第一、三象限
第二、四象限
典例精析
例1.已知反比例函数 的图象在第一、三象限内,则m的取值范围是_____.
m>2
例2.已知反比例函数 (k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的表达式;
解:∵反比例函数 (k为常数,k≠0)的图象经
过点 A(2,3),
∴把点A的坐标代入表达式,得 ,
解得k=6,
∴这个函数的表达式为 .
典例精析
解:∵反比例函数的表达式为 ,
∴6=xy.
分别把点B,C的坐标代入,
得(-1)×6=-6≠6,
则点B不在该函数图象上;
3×2=6,则点C在该函数图象上.
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由.
随堂练习
1.下图给出了反比例函数 和 的图象,你知道哪一个是 的图象吗?为什么?
(2)
2.如图,已知直线y=mx与双曲线 的一个交点坐标为
(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3)
B. (3,1)
C. (1,-3)
D. (-1,3)
x
y
O
3.已知函数y =(m-2)·xm2-5 是反比例函数.求m的值.
课堂总结
当k>0时,两支曲线分别位于一、三象限内;
当k<0时,两支曲线分别位于二、四象限内;
第六章 反比例函数
第2节 反比例函数的图象与性质(1)
学习目标
1.会用描点法画出反比例函数的图象,并掌握反比例函数图象的特征.(重点)
2.会利用反比例函数图象解决相关问题.(难点)
情景引入
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
3.还记得一次函数的图像与性质吗?
一般地,形如 ( k是常数, k ≠0 )的函数叫做反比例函数.
函数 正比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx(k是常数,k≠0)
直线(经过原点)
一、三象限
从左到右上升
y随x的增大而增大
二、四象限
从左到右下降
y随x的增大而减小
反比例函数
?
你还记得画函数图象的步骤吗?
① 列表;
②描点;
③连线。
反比例函数的图象
1—
问题:如何画反比例函数 的图象?
列表
描点
连线
解:列表如下
x -8 -4 -3 -2 -1 1 2 3 4 8
y
-1
-2
-4
-8
8
4
2
1
描点、连线:
x
-8 -7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8
y
-1
-2
-3
-4
-5
-6
-7
-8
87654321
用光滑的曲线顺次连接各点
想一想:你认为作反比例函数图象时应注意哪些问题
1.列表时,自变量的值可以选取一些互为相反数的值这样既可简化计算,又便于对称性描点;
2.列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
3.连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……
4.双曲线的两支都无限接近坐标轴,但永远不与坐标轴相交 .如图.
在图中的平面直角坐标系中画出反比例函数 的图象.
做一做
(1)观察 和 的图象,它们有什么相同点和不同点
(2)反比例函数 的图象在哪两个象限,由什么确定?
x
y
x
y
双曲线
轴对称图形,也是以原点为对称中心的中心对称图形.
O
O
议一议
相同点:1.两支曲线构成;
2.与坐标轴不相交;
3.图象自身关于原点成中心对称;
4.图象自身是轴对称图形.
不同点:的图象在第一、三象限;
的图象在第二、四象限.
形状: 反比例函数 的图象由两支曲线组成,因此称反比例函数 的图象为双曲线.
位置:由k决定:
当k>0时,两支曲线分别位于______________内;
当k<0时,两支曲线分别位于______________内.
第一、三象限
第二、四象限
典例精析
例1.已知反比例函数 的图象在第一、三象限内,则m的取值范围是_____.
m>2
例2.已知反比例函数 (k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的表达式;
解:∵反比例函数 (k为常数,k≠0)的图象经
过点 A(2,3),
∴把点A的坐标代入表达式,得 ,
解得k=6,
∴这个函数的表达式为 .
典例精析
解:∵反比例函数的表达式为 ,
∴6=xy.
分别把点B,C的坐标代入,
得(-1)×6=-6≠6,
则点B不在该函数图象上;
3×2=6,则点C在该函数图象上.
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由.
随堂练习
1.下图给出了反比例函数 和 的图象,你知道哪一个是 的图象吗?为什么?
(2)
2.如图,已知直线y=mx与双曲线 的一个交点坐标为
(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3)
B. (3,1)
C. (1,-3)
D. (-1,3)
x
y
O
3.已知函数y =(m-2)·xm2-5 是反比例函数.求m的值.
课堂总结
当k>0时,两支曲线分别位于一、三象限内;
当k<0时,两支曲线分别位于二、四象限内;
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
