华东师大版九年级数学上册 23.5位似图形课件 17张PPT
文档属性
| 名称 | 华东师大版九年级数学上册 23.5位似图形课件 17张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 718.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 22:05:17 | ||
图片预览





文档简介
(共17张PPT)
23.5
位
似
图
形
华师版
九年
级
数
学
课
件
learning target
学习目标
1.了解位似图形的概念与特征.
2.理解位似比与位似图形的关系.
3.会画位似图形并能利用位似解决一些相关的问题.
重、难点与关键
重点:了解位似图形的概念与特征.
难点:理解位似比与位似图形的关系,会画位似图形并能利用位似解决一些相关的问题.
关键:悟透位似的实质.
动手操作:
画一个三角形与原三角形的相似比为1:2,你是怎么画的?
Context import
情境导入
观察:
这些图形是什么关系?它们的对应边有什么关系?它们的对应角有什么关系?它们相似吗?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形.
这个点叫做位似中心.
位似图形概念:
Thinking promotion
思维提升
归纳:
Context import
情境导入
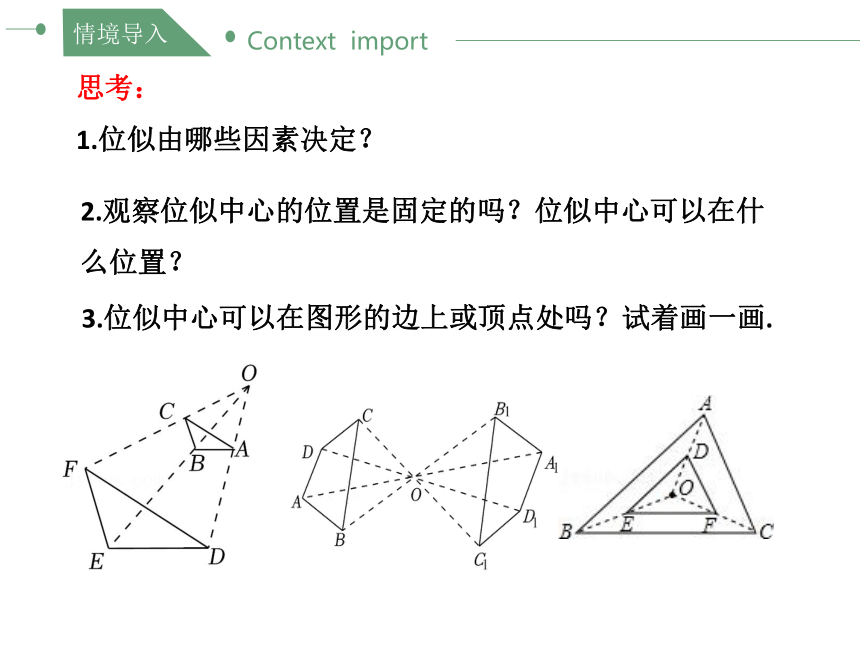
思考:
1.位似由哪些因素决定?
3.位似中心可以在图形的边上或顶点处吗?试着画一画.
2.观察位似中心的位置是固定的吗?位似中心可以在什么位置?
位似中心可以在图形的外部,也可以在图形的内部,也可以在图形的边上或顶点处.
Thinking promotion
思维提升
注意:位似中心在图形外部时,两个图形可以在位似中心的同侧,也可以在位似中心的异侧.
性质:位似图形上任意一对对应点到位似中心的距离之比
等于相似比.
归纳:
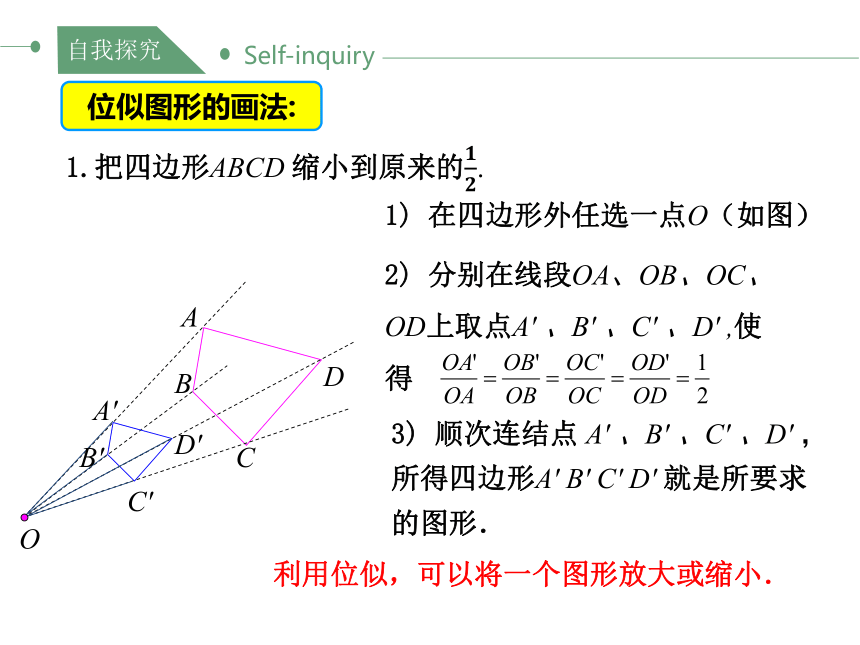
2) 分别在线段OA、OB、OC、OD上取点A' 、B' 、C' 、D' ,使得
3) 顺次连结点 A' 、B' 、C' 、D' ,所得四边形A' B' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
1.把四边形ABCD 缩小到原来的.
1) 在四边形外任选一点O(如图)
Self-inquiry
自我探究
位似图形的画法:
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A ' 、B ' 、C ' 、D ' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
Self-inquiry
自我探究
2.利用位似进行作图的关键是确定位似中心和关键点.
3.位似分为内位似和外位似,内位似的位似中心在连结两个对应点的线段上;外位似的位似中心在连结两个对应点的线段之外.
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.
Thinking promotion
思维提升
归纳:
例1:如图,将△ABC以点O为位似中心缩小得到△DEF,若OD=AD,则△ABC与△DEF的相似比是( )
解:∵△ABC以点O为位似中心缩小得到△DEF
∴△ABC与△DEF位似
∴DF∥AC,
∴△ODF∽△OAC,
∴
即△ABC与△DEF的相似比2:1.
掌握位似图形的概念,相似三角形的性质,图形的对应边平行是解题的关键.
Typical case analysis
典例分析
故选:B.
A.1:1 B.2:1 C.1:2 D.3:1
解题密码:
B
例2:如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法正确的有( )个.
①S△ABC:S△A'B'C'=1:2 ②AB:A'B'=1:2
③点A,O,A'三点在同一条直线上 ④BC∥B'C'
A.1 B.2 C.3 D.4
解:∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',
∴△ABC∽△A'B'C',相似比为1:2,点A,O,A'三点在同一条直线上,所以③正确;∴S△ABC:S△A'B'C'=1:4,所以①错误;AB:A'B'=1:2,所以②正确;OB:OB′=OC:OC′=1:2,而∠BOC=∠B′OC′∴△OBC∽△OB′C′,
∴∠OBC=∠OB′C′,∴BC∥B'C',所以④正确.
Typical case analysis
典例分析
故选:C.
位似的两个图形必须是相似形,对应点的连线都经过同一点是解题的关键.
解题密码:
C
1.如图,△OAB 和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
答:AB∥CD.
∵△OAB与△OCD是位似图形
∴△OAB ∽△OCD
∴∠OAB=∠C
∴AB∥CD.
解题密码:
Exchange discussion
交流讨论
根据位似变换的性质,求出两个三角形的对应角相
等,再由同位角相等得出两直线平行是解题的关键.
2.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A'B'C'D'E'.
D
B
E
C
O
A
●
●
●
●
Exchange discussion
交流讨论
解题密码:
根据位似图形的画法,位似比缩小一半是解题的关键.
●
●
A'
●
E'
●
D'
●
B'
●
C'
●
3.如图,在平面直角坐标系中,△A′B′C′与△ABC位似,位似中心为原点O.已知点A(﹣1,﹣1),C(﹣4,﹣1),A′C′=6,则点C′的坐标为( )
A.(2,2) B.(4,2) C.(6,3) D.(8,2)
解:∵△A′B′C′与△ABC位似
∴△A′B′C′∽△ABC
∵点A(﹣1,﹣1),C(﹣4,﹣1)
∴AC=﹣1﹣(﹣4)=3
∵A′C′=6
∴△A′B′C′与△ABC的相似比为2:1
∵C(﹣4,﹣1)
∴点C′的坐标为(8,2)
Exchange discussion
交流讨论
根据位似变换的性质,求出两个三角形的位似比是解题的关键.
故选:D.
解题密码:
D
1. 位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或
相似比;
(4)对应线段平行或者在一条直线上.
归纳:
Classroom summary
课堂小结
Method summary
方法总结
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.
2.利用位似进行作图的关键是确定位似中心和关键点.
3.位似中心可以在图形之外,也可在图形内或图形上.
23.5
位
似
图
形
华师版
九年
级
数
学
课
件
learning target
学习目标
1.了解位似图形的概念与特征.
2.理解位似比与位似图形的关系.
3.会画位似图形并能利用位似解决一些相关的问题.
重、难点与关键
重点:了解位似图形的概念与特征.
难点:理解位似比与位似图形的关系,会画位似图形并能利用位似解决一些相关的问题.
关键:悟透位似的实质.
动手操作:
画一个三角形与原三角形的相似比为1:2,你是怎么画的?
Context import
情境导入
观察:
这些图形是什么关系?它们的对应边有什么关系?它们的对应角有什么关系?它们相似吗?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形.
这个点叫做位似中心.
位似图形概念:
Thinking promotion
思维提升
归纳:
Context import
情境导入
思考:
1.位似由哪些因素决定?
3.位似中心可以在图形的边上或顶点处吗?试着画一画.
2.观察位似中心的位置是固定的吗?位似中心可以在什么位置?
位似中心可以在图形的外部,也可以在图形的内部,也可以在图形的边上或顶点处.
Thinking promotion
思维提升
注意:位似中心在图形外部时,两个图形可以在位似中心的同侧,也可以在位似中心的异侧.
性质:位似图形上任意一对对应点到位似中心的距离之比
等于相似比.
归纳:
2) 分别在线段OA、OB、OC、OD上取点A' 、B' 、C' 、D' ,使得
3) 顺次连结点 A' 、B' 、C' 、D' ,所得四边形A' B' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
1.把四边形ABCD 缩小到原来的.
1) 在四边形外任选一点O(如图)
Self-inquiry
自我探究
位似图形的画法:
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A ' 、B ' 、C ' 、D ' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
Self-inquiry
自我探究
2.利用位似进行作图的关键是确定位似中心和关键点.
3.位似分为内位似和外位似,内位似的位似中心在连结两个对应点的线段上;外位似的位似中心在连结两个对应点的线段之外.
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.
Thinking promotion
思维提升
归纳:
例1:如图,将△ABC以点O为位似中心缩小得到△DEF,若OD=AD,则△ABC与△DEF的相似比是( )
解:∵△ABC以点O为位似中心缩小得到△DEF
∴△ABC与△DEF位似
∴DF∥AC,
∴△ODF∽△OAC,
∴
即△ABC与△DEF的相似比2:1.
掌握位似图形的概念,相似三角形的性质,图形的对应边平行是解题的关键.
Typical case analysis
典例分析
故选:B.
A.1:1 B.2:1 C.1:2 D.3:1
解题密码:
B
例2:如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法正确的有( )个.
①S△ABC:S△A'B'C'=1:2 ②AB:A'B'=1:2
③点A,O,A'三点在同一条直线上 ④BC∥B'C'
A.1 B.2 C.3 D.4
解:∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',
∴△ABC∽△A'B'C',相似比为1:2,点A,O,A'三点在同一条直线上,所以③正确;∴S△ABC:S△A'B'C'=1:4,所以①错误;AB:A'B'=1:2,所以②正确;OB:OB′=OC:OC′=1:2,而∠BOC=∠B′OC′∴△OBC∽△OB′C′,
∴∠OBC=∠OB′C′,∴BC∥B'C',所以④正确.
Typical case analysis
典例分析
故选:C.
位似的两个图形必须是相似形,对应点的连线都经过同一点是解题的关键.
解题密码:
C
1.如图,△OAB 和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
答:AB∥CD.
∵△OAB与△OCD是位似图形
∴△OAB ∽△OCD
∴∠OAB=∠C
∴AB∥CD.
解题密码:
Exchange discussion
交流讨论
根据位似变换的性质,求出两个三角形的对应角相
等,再由同位角相等得出两直线平行是解题的关键.
2.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A'B'C'D'E'.
D
B
E
C
O
A
●
●
●
●
Exchange discussion
交流讨论
解题密码:
根据位似图形的画法,位似比缩小一半是解题的关键.
●
●
A'
●
E'
●
D'
●
B'
●
C'
●
3.如图,在平面直角坐标系中,△A′B′C′与△ABC位似,位似中心为原点O.已知点A(﹣1,﹣1),C(﹣4,﹣1),A′C′=6,则点C′的坐标为( )
A.(2,2) B.(4,2) C.(6,3) D.(8,2)
解:∵△A′B′C′与△ABC位似
∴△A′B′C′∽△ABC
∵点A(﹣1,﹣1),C(﹣4,﹣1)
∴AC=﹣1﹣(﹣4)=3
∵A′C′=6
∴△A′B′C′与△ABC的相似比为2:1
∵C(﹣4,﹣1)
∴点C′的坐标为(8,2)
Exchange discussion
交流讨论
根据位似变换的性质,求出两个三角形的位似比是解题的关键.
故选:D.
解题密码:
D
1. 位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或
相似比;
(4)对应线段平行或者在一条直线上.
归纳:
Classroom summary
课堂小结
Method summary
方法总结
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.
2.利用位似进行作图的关键是确定位似中心和关键点.
3.位似中心可以在图形之外,也可在图形内或图形上.
