8.3再探实际问题与二元一次方程组3
文档属性
| 名称 | 8.3再探实际问题与二元一次方程组3 |  | |
| 格式 | rar | ||
| 文件大小 | 763.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-22 00:35:00 | ||
图片预览


文档简介
课件12张PPT。再探实际问题与二元一次方程组(探究3)1、公路的运价为1.5元/(吨·千米),
里程为10km,货物重量为200吨,
则公路运费= .1.5×10×2002、铁路的运价为1.2元/(吨·千米),
原料重量为100吨,里程为20km,
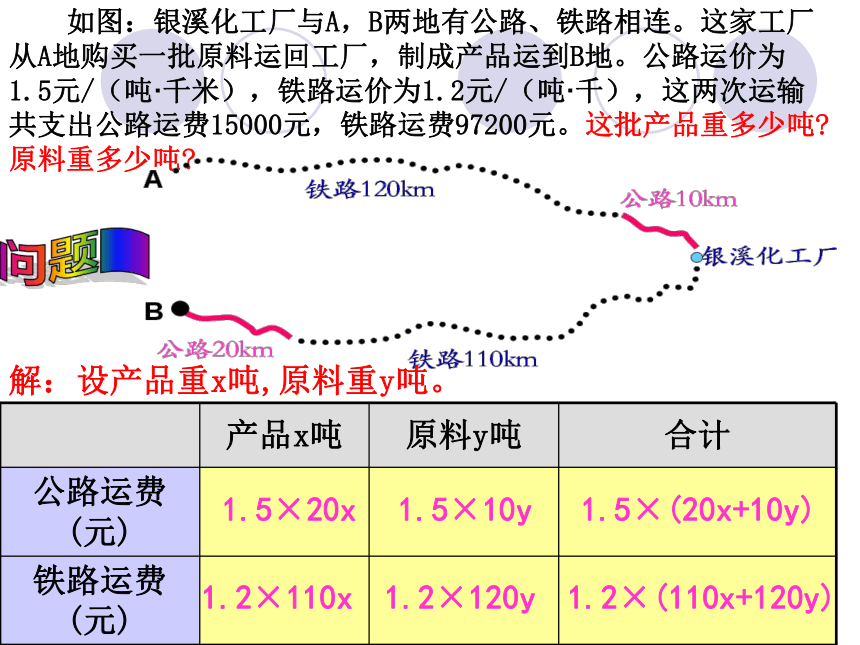
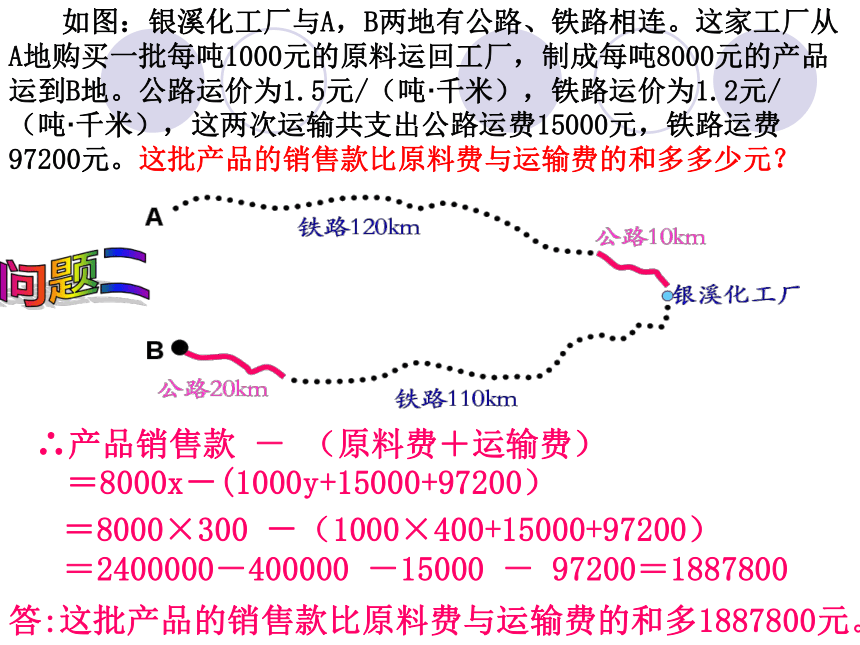
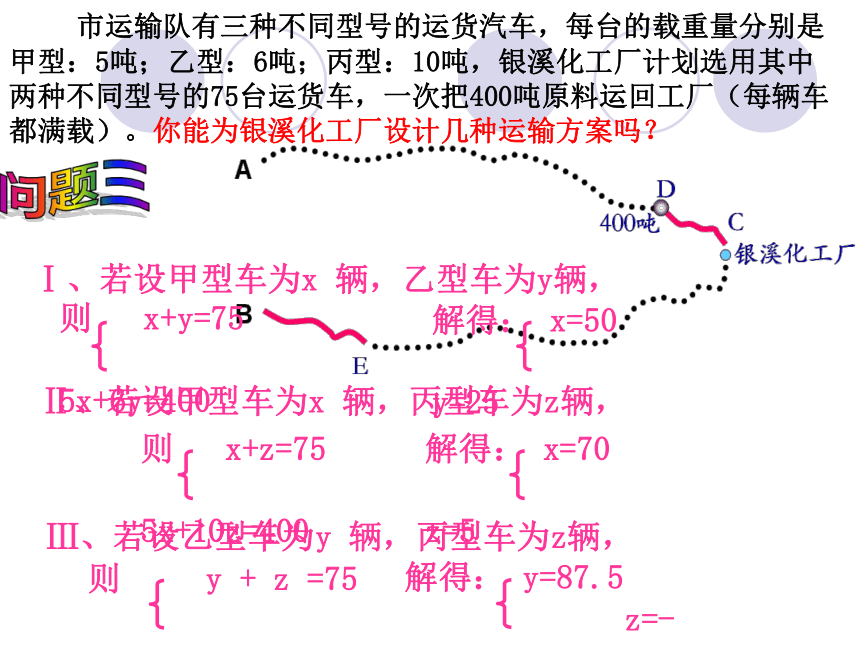
则铁路运费= .1.2×20×100 如图:银溪化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品重多少吨?原料重多少吨?1.5×20x1.5×10y1.5×(20x+10y)1.2×110x1.2×120y1.2×(110x+120y)解:设产品重x吨,原料重y吨。问题一 如图:银溪化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?∴产品销售款 - (原料费+运输费)=8000x-(1000y+15000+97200)=8000×300 -(1000×400+15000+97200)=2400000-400000 -15000 - 97200=1887800答:这批产品的销售款比原料费与运输费的和多1887800元。问题二 市运输队有三种不同型号的运货汽车,每台的载重量分别是甲型:5吨;乙型:6吨;丙型:10吨,银溪化工厂计划选用其中两种不同型号的75台运货车,一次把400吨原料运回工厂(每辆车都满载)。你能为银溪化工厂设计几种运输方案吗?Ⅰ、若设甲型车为x 辆,乙型车为y辆,解得: x=50
y=25 则 x+y=75
5x+6y=400
Ⅱ、若设甲型车为x 辆,丙型车为z辆,解得: x=70
z=5则 x+z=75
5x+10z=400Ⅲ、若设乙型车为y 辆,丙型车为z辆,解得: y=87.5
z=-12.5
则 y + z =75
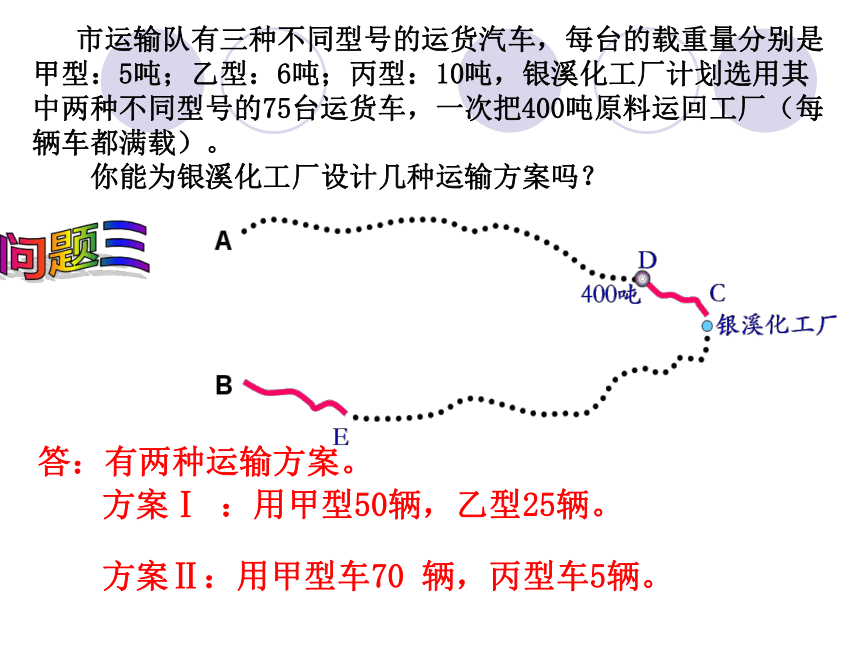
6y+10z=400问题三 市运输队有三种不同型号的运货汽车,每台的载重量分别是甲型:5吨;乙型:6吨;丙型:10吨,银溪化工厂计划选用其中两种不同型号的75台运货车,一次把400吨原料运回工厂(每辆车都满载)。
你能为银溪化工厂设计几种运输方案吗?答:有两种运输方案。方案Ⅰ :用甲型50辆,乙型25辆。方案Ⅱ:用甲型车70 辆,丙型车5辆。问题三作业:一旅游者从下午2时步行到晚上7时,他先走平路,然后登山,到山顶后又沿原路下山回到出发点,已知他走平路时每小时走4千米,爬山时每小时走3千米,下坡时每小时走6千米,问旅游者一共走了多少路?例:从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行33分,从乙地到甲地需行23.4分,从甲地到乙地全程是多少?1、你能用图形表示这个问题吗?2、你能自己设计一个表格,显示题中各个量吗?3、若设甲到乙上坡路长为x千米,平路长为y千米,你能填出来吗?X
323.4
60y
4X
533
66y
4练一练:1、甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每小时各走多少千米?2、一列快车长70米,慢车长80米。若两车同向而行,快车从追上慢车到完全离开所用时间(即会车时间)为20秒。若两车相向而行,则两车从相遇到离开时间4秒,求两车每小时各行多少千米?实际问题设未知数,列方程组数学问题
(二元一次方程组)数学问题的解
(x=a , y=b)解 方 程 组代入法
加减法
(消元)实际问题的答案检验 1、请编一道应用题(不需要求解),这道应用题应满足
(1)能用二元一次方程组求解。
(2)要符合实际意义。
2、在问题三的条件下,同时用甲、乙、丙三种不同型号的运货车45辆,一次运货400吨,有几种运输方案。(每辆车都满载)作业:开放式问题小结:
通过今天的学习,你们有什么收获吗?
作业:
1、必做题:课本116页课本116页第1(2)题,第6题
2、选做题:课本117页第9题
里程为10km,货物重量为200吨,
则公路运费= .1.5×10×2002、铁路的运价为1.2元/(吨·千米),
原料重量为100吨,里程为20km,
则铁路运费= .1.2×20×100 如图:银溪化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品重多少吨?原料重多少吨?1.5×20x1.5×10y1.5×(20x+10y)1.2×110x1.2×120y1.2×(110x+120y)解:设产品重x吨,原料重y吨。问题一 如图:银溪化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?∴产品销售款 - (原料费+运输费)=8000x-(1000y+15000+97200)=8000×300 -(1000×400+15000+97200)=2400000-400000 -15000 - 97200=1887800答:这批产品的销售款比原料费与运输费的和多1887800元。问题二 市运输队有三种不同型号的运货汽车,每台的载重量分别是甲型:5吨;乙型:6吨;丙型:10吨,银溪化工厂计划选用其中两种不同型号的75台运货车,一次把400吨原料运回工厂(每辆车都满载)。你能为银溪化工厂设计几种运输方案吗?Ⅰ、若设甲型车为x 辆,乙型车为y辆,解得: x=50
y=25 则 x+y=75
5x+6y=400
Ⅱ、若设甲型车为x 辆,丙型车为z辆,解得: x=70
z=5则 x+z=75
5x+10z=400Ⅲ、若设乙型车为y 辆,丙型车为z辆,解得: y=87.5
z=-12.5
则 y + z =75
6y+10z=400问题三 市运输队有三种不同型号的运货汽车,每台的载重量分别是甲型:5吨;乙型:6吨;丙型:10吨,银溪化工厂计划选用其中两种不同型号的75台运货车,一次把400吨原料运回工厂(每辆车都满载)。
你能为银溪化工厂设计几种运输方案吗?答:有两种运输方案。方案Ⅰ :用甲型50辆,乙型25辆。方案Ⅱ:用甲型车70 辆,丙型车5辆。问题三作业:一旅游者从下午2时步行到晚上7时,他先走平路,然后登山,到山顶后又沿原路下山回到出发点,已知他走平路时每小时走4千米,爬山时每小时走3千米,下坡时每小时走6千米,问旅游者一共走了多少路?例:从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行33分,从乙地到甲地需行23.4分,从甲地到乙地全程是多少?1、你能用图形表示这个问题吗?2、你能自己设计一个表格,显示题中各个量吗?3、若设甲到乙上坡路长为x千米,平路长为y千米,你能填出来吗?X
323.4
60y
4X
533
66y
4练一练:1、甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每小时各走多少千米?2、一列快车长70米,慢车长80米。若两车同向而行,快车从追上慢车到完全离开所用时间(即会车时间)为20秒。若两车相向而行,则两车从相遇到离开时间4秒,求两车每小时各行多少千米?实际问题设未知数,列方程组数学问题
(二元一次方程组)数学问题的解
(x=a , y=b)解 方 程 组代入法
加减法
(消元)实际问题的答案检验 1、请编一道应用题(不需要求解),这道应用题应满足
(1)能用二元一次方程组求解。
(2)要符合实际意义。
2、在问题三的条件下,同时用甲、乙、丙三种不同型号的运货车45辆,一次运货400吨,有几种运输方案。(每辆车都满载)作业:开放式问题小结:
通过今天的学习,你们有什么收获吗?
作业:
1、必做题:课本116页课本116页第1(2)题,第6题
2、选做题:课本117页第9题
