17.1勾股定理的实际应用2课件
文档属性
| 名称 | 17.1勾股定理的实际应用2课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-13 00:00:00 | ||
图片预览










文档简介
课件38张PPT。数 学新课标(RJ) 八年级下册第十七章 勾股定理17.1 勾股定理第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用教材重难处理教材【第29页第13题】分层分析
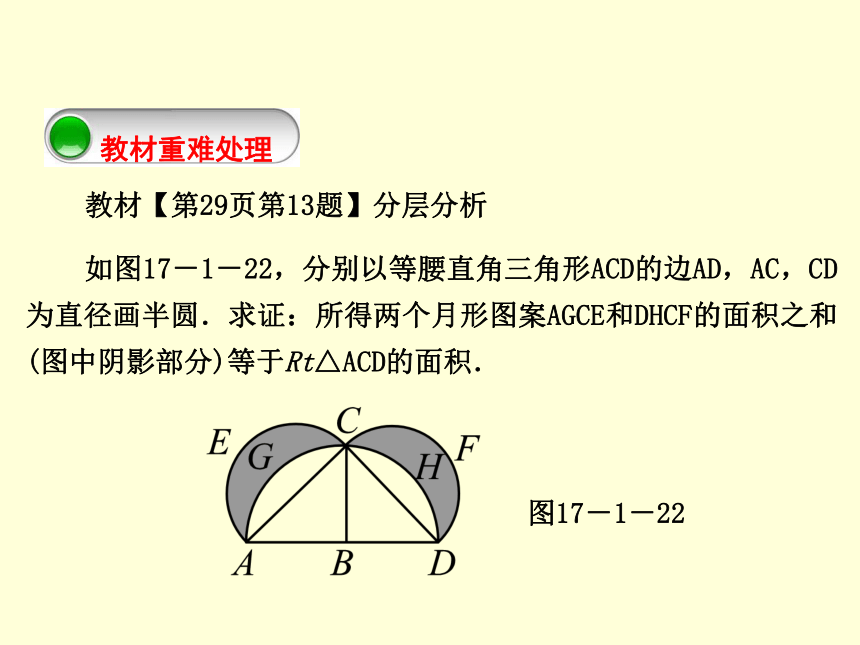
如图17-1-22,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.求证:所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.图17-1-22第2课时 勾股定理的实际应用分析:(1)从图中看,等腰直角三角形ACD的两直角边(腰)是____,____,斜边是____.
(2)由勾股定理,知AC,CD,AD满足的关系式为___________________________.
(3)分别以边AC,CD,AD为直径的半圆的面积分别表示为
______________,__________,________.等腰直角三角形
ACD的面积表示为__________________________.ACCDADAC2+CD2=AD2第2课时 勾股定理的实际应用(4)观察图形:两个月形图案AGCE和DHCF的面积和等于______________________________________________________________________________________________________________,
即
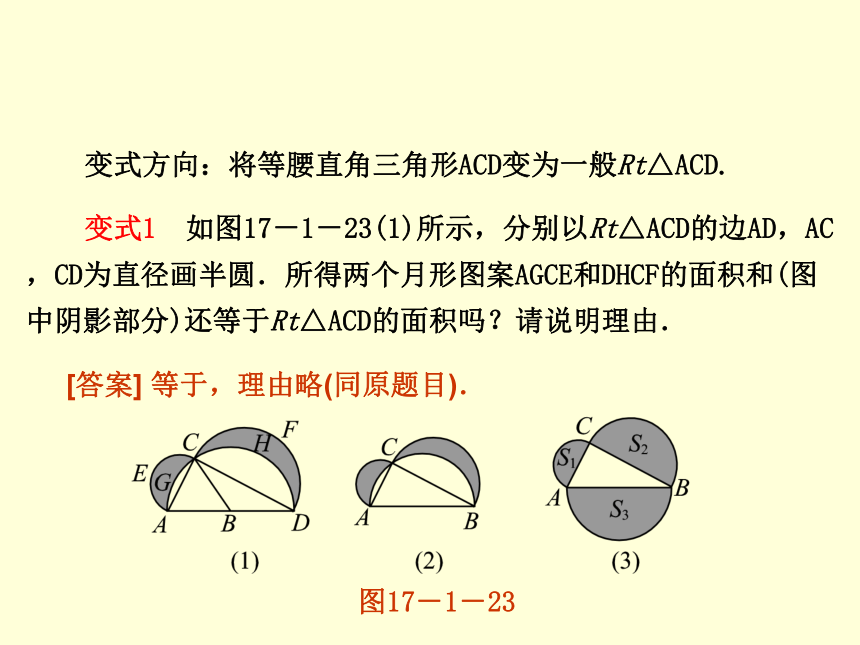
___________________________________________________.以边AC,CD为直径的两个半圆的面积和加上等腰直角三角形ACD的面积再减去以边AD为直径的半圆的面积 第2课时 勾股定理的实际应用变式方向:将等腰直角三角形ACD变为一般Rt△ACD.
变式1 如图17-1-23(1)所示,分别以Rt△ACD的边AD,AC,CD为直径画半圆.所得两个月形图案AGCE和DHCF的面积和(图中阴影部分)还等于Rt△ACD的面积吗?请说明理由.[答案] 等于,理由略(同原题目).图17-1-23第2课时 勾股定理的实际应用变式2 如图(2),Rt△ABC中,AC=5,BC=12,分别以它的三边为直径作三个半圆,则阴影部分的面积为____.
变式3 如图(3),∠C=90°,图中阴影部分的三个半圆的面积有什么关系?
30[答案] S1+S2=S3.探 究 新 知 ? 活动1 知识准备第2课时 勾股定理的实际应用1.32+42=____2;52+122=____2.
2.在直角三角形中,两条直角边的_________等于斜边的平方.
3.两点之间,______最短.513平方和线段 ? 活动2 教材导学 第2课时 勾股定理的实际应用1.如图17-1-24,有一只小鸟在一棵高4 m的小树梢上捉虫子,它的伙伴在离该树12 m,高20 m的一棵大树的树梢上发出友好的叫声,该小鸟立刻以4 m/s的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?图17-1-24第2课时 勾股定理的实际应用解:如图17-1-25所示,
根据题意,得AC=20-4=16(m),BC=12 m.
在Rt△ABC中,根据勾股定理,得AC2+BC2=AB2,即
162+122=AB2,
解得AB=20,
则这只小鸟所用的时间至少是20÷4=5(s).图17-1-25 第2课时 勾股定理的实际应用2.有一个长、宽、高分别为3 cm,4 cm,12 cm的长方体纸盒,你能在里面放下一根长为14 cm的铅笔吗?
解:不能.新 知 梳 理 ? 知识点 立体图形中表面上两点之间的最短距离 第2课时 勾股定理的实际应用重难互动探究探究问题一 勾股定理的实际应用 第2课时 勾股定理的实际应用图17-1-26第2课时 勾股定理的实际应用[解析] 设CD=x米,在Rt△ABC中,可利用勾股定理建立等量关系,列方程,并解方程求解. 第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用图17-1-27第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用[归纳总结] 挖掘实际问题中的直角,把实际问题转化到直角三角形中,应用勾股定理计算后,回答实际问题.第2课时 勾股定理的实际应用探究问题二 求平面上两点之间的最短距离 例3 如图17-1-28所示,一个牧童在小河南4 km的A处牧马,而他正位于他的小屋B的西8 km北7 km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少? 第2课时 勾股定理的实际应用 图17-1-28 图17-1-29第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用[归纳总结] “两点一直线” 型最短路径问题有两种情况:(1)两点在一直线异侧时,连接两点与直线有一个交点,交点就是所求的点.(2)两点在一直线同侧时,作其中一点关于直线的对称点,对称点与另一点的连线与直线相交.最短路线为“一点→交点→另一点”.第2课时 勾股定理的实际应用[归纳总结] 确定立体图形表面上的最短路径问题,其解题思路是将立体图形展开,转化为平面图形,并借助勾股定理解决.当长方体的长、宽、高不同时,不同表面上两点之间的距离分三种情况讨论,展开方式不同,两点间的距离也可能不同.例1、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512一、台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.二、圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)三、正方体中的最值问题例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题练习:◆在长30cm、宽50 cm、高40 cm的木箱中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD305040图①305040CDA.B.ADCB305040CCDA.B.图②304050CCDA.B.图③50ADCB4030304050第2课时 勾股定理的实际应用探究问题三 求立体图形中表面上两点之间的最短距离 例4 如图17-1-30所示,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,求这只蚂蚁要爬行的最短距离.[解析] 沿长方体表面从点A爬到点B,考虑路线最短的问题有三种途径:(1)从右侧面和前面走.(2)从右侧面和上底面走.(3)从后侧面和上底面走,由两点之间线段最短来确定路径.第2课时 勾股定理的实际应用①②图17-1-31③第2课时 勾股定理的实际应用小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
如图17-1-22,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.求证:所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.图17-1-22第2课时 勾股定理的实际应用分析:(1)从图中看,等腰直角三角形ACD的两直角边(腰)是____,____,斜边是____.
(2)由勾股定理,知AC,CD,AD满足的关系式为___________________________.
(3)分别以边AC,CD,AD为直径的半圆的面积分别表示为
______________,__________,________.等腰直角三角形
ACD的面积表示为__________________________.ACCDADAC2+CD2=AD2第2课时 勾股定理的实际应用(4)观察图形:两个月形图案AGCE和DHCF的面积和等于______________________________________________________________________________________________________________,
即
___________________________________________________.以边AC,CD为直径的两个半圆的面积和加上等腰直角三角形ACD的面积再减去以边AD为直径的半圆的面积 第2课时 勾股定理的实际应用变式方向:将等腰直角三角形ACD变为一般Rt△ACD.
变式1 如图17-1-23(1)所示,分别以Rt△ACD的边AD,AC,CD为直径画半圆.所得两个月形图案AGCE和DHCF的面积和(图中阴影部分)还等于Rt△ACD的面积吗?请说明理由.[答案] 等于,理由略(同原题目).图17-1-23第2课时 勾股定理的实际应用变式2 如图(2),Rt△ABC中,AC=5,BC=12,分别以它的三边为直径作三个半圆,则阴影部分的面积为____.
变式3 如图(3),∠C=90°,图中阴影部分的三个半圆的面积有什么关系?
30[答案] S1+S2=S3.探 究 新 知 ? 活动1 知识准备第2课时 勾股定理的实际应用1.32+42=____2;52+122=____2.
2.在直角三角形中,两条直角边的_________等于斜边的平方.
3.两点之间,______最短.513平方和线段 ? 活动2 教材导学 第2课时 勾股定理的实际应用1.如图17-1-24,有一只小鸟在一棵高4 m的小树梢上捉虫子,它的伙伴在离该树12 m,高20 m的一棵大树的树梢上发出友好的叫声,该小鸟立刻以4 m/s的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?图17-1-24第2课时 勾股定理的实际应用解:如图17-1-25所示,
根据题意,得AC=20-4=16(m),BC=12 m.
在Rt△ABC中,根据勾股定理,得AC2+BC2=AB2,即
162+122=AB2,
解得AB=20,
则这只小鸟所用的时间至少是20÷4=5(s).图17-1-25 第2课时 勾股定理的实际应用2.有一个长、宽、高分别为3 cm,4 cm,12 cm的长方体纸盒,你能在里面放下一根长为14 cm的铅笔吗?
解:不能.新 知 梳 理 ? 知识点 立体图形中表面上两点之间的最短距离 第2课时 勾股定理的实际应用重难互动探究探究问题一 勾股定理的实际应用 第2课时 勾股定理的实际应用图17-1-26第2课时 勾股定理的实际应用[解析] 设CD=x米,在Rt△ABC中,可利用勾股定理建立等量关系,列方程,并解方程求解. 第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用图17-1-27第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用[归纳总结] 挖掘实际问题中的直角,把实际问题转化到直角三角形中,应用勾股定理计算后,回答实际问题.第2课时 勾股定理的实际应用探究问题二 求平面上两点之间的最短距离 例3 如图17-1-28所示,一个牧童在小河南4 km的A处牧马,而他正位于他的小屋B的西8 km北7 km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少? 第2课时 勾股定理的实际应用 图17-1-28 图17-1-29第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用第2课时 勾股定理的实际应用[归纳总结] “两点一直线” 型最短路径问题有两种情况:(1)两点在一直线异侧时,连接两点与直线有一个交点,交点就是所求的点.(2)两点在一直线同侧时,作其中一点关于直线的对称点,对称点与另一点的连线与直线相交.最短路线为“一点→交点→另一点”.第2课时 勾股定理的实际应用[归纳总结] 确定立体图形表面上的最短路径问题,其解题思路是将立体图形展开,转化为平面图形,并借助勾股定理解决.当长方体的长、宽、高不同时,不同表面上两点之间的距离分三种情况讨论,展开方式不同,两点间的距离也可能不同.例1、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512一、台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.二、圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)三、正方体中的最值问题例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题练习:◆在长30cm、宽50 cm、高40 cm的木箱中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD305040图①305040CDA.B.ADCB305040CCDA.B.图②304050CCDA.B.图③50ADCB4030304050第2课时 勾股定理的实际应用探究问题三 求立体图形中表面上两点之间的最短距离 例4 如图17-1-30所示,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,求这只蚂蚁要爬行的最短距离.[解析] 沿长方体表面从点A爬到点B,考虑路线最短的问题有三种途径:(1)从右侧面和前面走.(2)从右侧面和上底面走.(3)从后侧面和上底面走,由两点之间线段最短来确定路径.第2课时 勾股定理的实际应用①②图17-1-31③第2课时 勾股定理的实际应用小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
