17.1勾股定理的计算、作图3课件
文档属性
| 名称 | 17.1勾股定理的计算、作图3课件 |  | |
| 格式 | zip | ||
| 文件大小 | 658.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-13 08:54:03 | ||
图片预览








文档简介
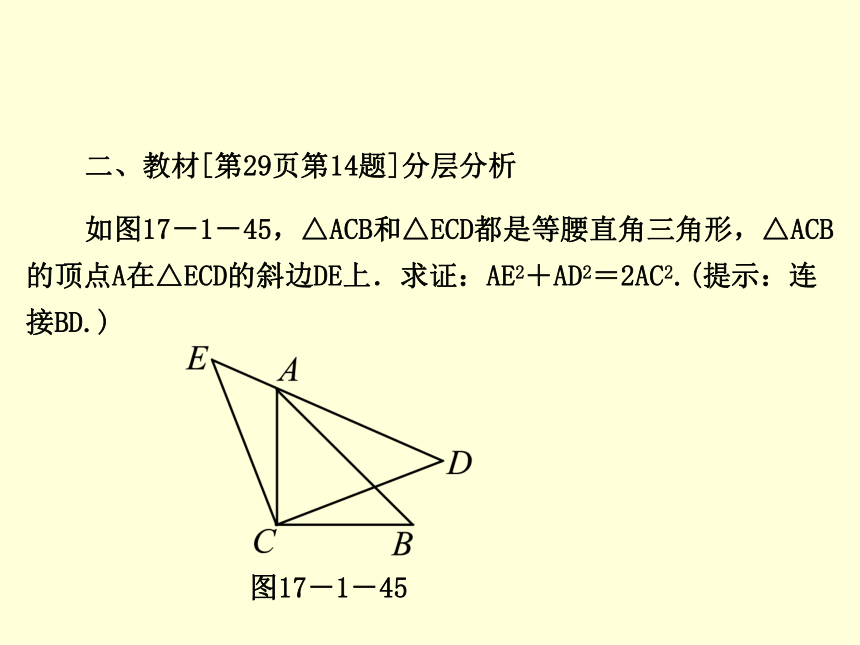
课件22张PPT。数 学新课标(RJ) 八年级下册第3课时 勾股定理的计算、作图第十七章 勾股定理17.1 勾股定理第3课时 勾股定理的计算、作图教材重难处理a2+b2=c2 a2+b2=13 13=4+9 2 3 2 2 第3课时 勾股定理的计算、作图32正半轴 2负半轴 第3课时 勾股定理的计算、作图二、教材[第29页第14题]分层分析
如图17-1-45,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.求证:AE2+AD2=2AC2.(提示:连接BD.)图17-1-45第3课时 勾股定理的计算、作图(1)因为△ACB是等腰直角三角形,结合图形可知斜边是AB,两直角边是AC,BC,由勾股定理,知_________________,即__________________________;
(2)欲证AE2+AD2=2AC2,由(1)可知,只需证__________________________;
(3)结合图形,点A,D,E在一条直线上,不能构成三角形,而点A,B,D三点可以构成三角形,因此可以考虑连接BD,只需证得_______________________________即可;AC2+BC2=AB22AC2=AB2或2BC2=AB2AE2+AD2=AB2BD=AE,且∠ADB=90°第3课时 勾股定理的计算、作图(4)要证BD=AE,可以考虑证明它们所在的___________和________全等,有哪些条件?由题意,显然有两组对应边,即_____________________________,夹角________________________________________________,显然两角相等;△BCD△ACEAC=BC,EC=DC∠BCD=90°-∠ACD,∠ACE=90°-∠ACD第3课时 勾股定理的计算、作图(5)证得△BCD和△ACE全等后,显然BD=AE,能证得∠ADB=90°吗?
[答案] 由题意,∠E=45°,∠EDC=45°,而∠ADB=∠EDC+∠CDB,∠CDB=∠E=45°,所以∠ADB=90°.从而结论得证.探 究 新 知 ? 活动1 知识准备第3课时 勾股定理的计算、作图 ? 活动2 教材导学 第3课时 勾股定理的计算、作图1.根据图17-1-46填空:
x=____,y=____,z=____,w=____.图17-1-462第3课时 勾股定理的计算、作图 2.按照图中的规律一直作下去,你能说出第n个小直角三角形的各边长和面积吗?新 知 梳 理 ? 知识点 在数轴上画出表示无理数的点 第3课时 勾股定理的计算、作图重难互动探究探究问题一 在数轴上画出表示无理数的点 第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图探究问题二 勾股定理的应用 第3课时 勾股定理的计算、作图[解析] 由题意,折叠后,AF=AD,DE=EF,可设EC=x cm,则DE=(8-x)cm.在Rt△ABF中,AF=10 cm,AB=8 cm,根据勾股定理,可知BF=6 cm,所以CF=4 cm.在Rt△CEF中,根据勾股定理可得关于x的方程.第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图[归纳总结] 1.勾股定理在三角形中的应用
(1)添线应用
应用勾股定理的前提条件是在直角三角形中,题目中若没有直角三角形,则可以通过作高等,把斜三角形的问题转化为直角三角形的问题,应用勾股定理求解.
(2)借助方程应用
题目中虽然有直角三角形,但是已知线段的长不完全是直角三角形的边,可以设出直角三角形的边,通过建立方程,解答这类计算问题.第3课时 勾股定理的计算、作图2.勾股定理在四边形中的应用
(1)梯形的问题,通常通过作高,应用勾股定理.
(2)任意四边形的问题,通常连接对角线等,转化成直角三角形的问题,再应用勾股定理.
长方形、直角三角形都是常见的平面图形,因为都含有直角,所以常常用到勾股定理.折叠问题常常将条件集中于一个直角三角形,然后利用勾股定理构建方程,求线段的长.
如图17-1-45,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.求证:AE2+AD2=2AC2.(提示:连接BD.)图17-1-45第3课时 勾股定理的计算、作图(1)因为△ACB是等腰直角三角形,结合图形可知斜边是AB,两直角边是AC,BC,由勾股定理,知_________________,即__________________________;
(2)欲证AE2+AD2=2AC2,由(1)可知,只需证__________________________;
(3)结合图形,点A,D,E在一条直线上,不能构成三角形,而点A,B,D三点可以构成三角形,因此可以考虑连接BD,只需证得_______________________________即可;AC2+BC2=AB22AC2=AB2或2BC2=AB2AE2+AD2=AB2BD=AE,且∠ADB=90°第3课时 勾股定理的计算、作图(4)要证BD=AE,可以考虑证明它们所在的___________和________全等,有哪些条件?由题意,显然有两组对应边,即_____________________________,夹角________________________________________________,显然两角相等;△BCD△ACEAC=BC,EC=DC∠BCD=90°-∠ACD,∠ACE=90°-∠ACD第3课时 勾股定理的计算、作图(5)证得△BCD和△ACE全等后,显然BD=AE,能证得∠ADB=90°吗?
[答案] 由题意,∠E=45°,∠EDC=45°,而∠ADB=∠EDC+∠CDB,∠CDB=∠E=45°,所以∠ADB=90°.从而结论得证.探 究 新 知 ? 活动1 知识准备第3课时 勾股定理的计算、作图 ? 活动2 教材导学 第3课时 勾股定理的计算、作图1.根据图17-1-46填空:
x=____,y=____,z=____,w=____.图17-1-462第3课时 勾股定理的计算、作图 2.按照图中的规律一直作下去,你能说出第n个小直角三角形的各边长和面积吗?新 知 梳 理 ? 知识点 在数轴上画出表示无理数的点 第3课时 勾股定理的计算、作图重难互动探究探究问题一 在数轴上画出表示无理数的点 第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图探究问题二 勾股定理的应用 第3课时 勾股定理的计算、作图[解析] 由题意,折叠后,AF=AD,DE=EF,可设EC=x cm,则DE=(8-x)cm.在Rt△ABF中,AF=10 cm,AB=8 cm,根据勾股定理,可知BF=6 cm,所以CF=4 cm.在Rt△CEF中,根据勾股定理可得关于x的方程.第3课时 勾股定理的计算、作图第3课时 勾股定理的计算、作图[归纳总结] 1.勾股定理在三角形中的应用
(1)添线应用
应用勾股定理的前提条件是在直角三角形中,题目中若没有直角三角形,则可以通过作高等,把斜三角形的问题转化为直角三角形的问题,应用勾股定理求解.
(2)借助方程应用
题目中虽然有直角三角形,但是已知线段的长不完全是直角三角形的边,可以设出直角三角形的边,通过建立方程,解答这类计算问题.第3课时 勾股定理的计算、作图2.勾股定理在四边形中的应用
(1)梯形的问题,通常通过作高,应用勾股定理.
(2)任意四边形的问题,通常连接对角线等,转化成直角三角形的问题,再应用勾股定理.
长方形、直角三角形都是常见的平面图形,因为都含有直角,所以常常用到勾股定理.折叠问题常常将条件集中于一个直角三角形,然后利用勾股定理构建方程,求线段的长.
