华师版秋学期九年级上册数学第24章 解直角三角形《测量》专题训练(含答案)
文档属性
| 名称 | 华师版秋学期九年级上册数学第24章 解直角三角形《测量》专题训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 00:00:00 | ||
图片预览

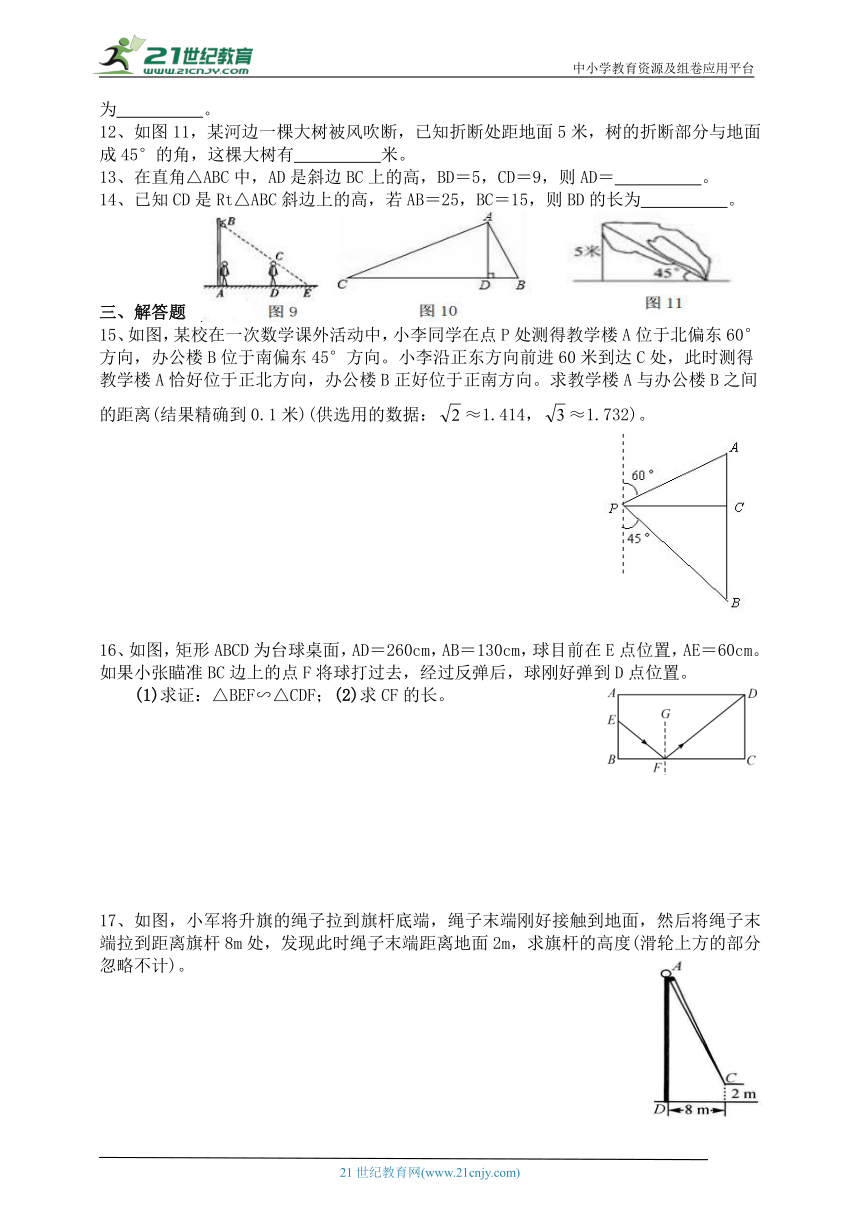

文档简介
中小学教育资源及组卷应用平台
华师版秋学期九年级上册数学《测量》专题训练
一、选择题
1、如图1,一场暴风雨过后,垂直于地面的一棵树在距地面2米处折断,树尖B恰好碰到地面,经测量AB=3米,则树高为( )
A.米 B.米 C.(+2)米 D.5米
2、某科技兴趣小组为测量学校旗杆AC的高度,在点F竖立一根长为1.5米的标杆DF,如图2所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影长BC的长度为6米,那么旗杆AC的高度为( )
A.5.5米 B.7米 C.8.5米 D.9米
3、如图3,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上。若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
4、如图4,李四要测量河内小岛B到河边公路的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路的距离为( )米。
A.25 B.25 C. D.25+25
5、如图5,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=6,CD=2,则AD为( )
A.2 B.2 C.3 D.2.5
6、如图6,经测BE=60m,CE=30m,CD=35m,则河的宽度AB的长为( )
A.30m B.35m C.60m D.70m
7、如图7,有两棵树,一棵高10m,另一棵高4m,两树相距8m。一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行( )
A.8m B.10m C.12m D.14m
8、如图8所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.a C.2a D.3a
二、填空题
9、在某时刻的阳光照耀下,身高160cm的小花的影长为80cm,她身旁的旗杆影长10m,则旗杆高为 m。
10、如图9,小军从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小军的身高为1.6米,那么路灯离地面的高度AB是 米。
11、如图10,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 。
12、如图11,某河边一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米。
13、在直角△ABC中,AD是斜边BC上的高,BD=5,CD=9,则AD= 。
14、已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 。
三、解答题
15、如图,某校在一次数学课外活动中,小李同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向。小李沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向。求教学楼A与办公楼B之间的距离(结果精确到0.1米)(供选用的数据:≈1.414,≈1.732)。
16、如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm。如果小张瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置。
(1)求证:△BEF∽△CDF;(2)求CF的长。
17、如图,小军将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,求旗杆的高度(滑轮上方的部分忽略不计)。
华师版秋学期九年级上册数学《测量》专题训练答案
一、选择题
1、如图1,一场暴风雨过后,垂直于地面的一棵树在距地面2米处折断,树尖B恰好碰到地面,经测量AB=3米,则树高为( )
A.米 B.米 C.(+2)米 D.5米
答案:C
2、某科技兴趣小组为测量学校旗杆AC的高度,在点F竖立一根长为1.5米的标杆DF,如图2所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影长BC的长度为6米,那么旗杆AC的高度为( )
A.5.5米 B.7米 C.8.5米 D.9米
答案:D
3、如图3,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上。若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
答案:C
4、如图4,李四要测量河内小岛B到河边公路的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路的距离为( )米。
A.25 B.25 C. D.25+25
答案:B
5、如图5,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=6,CD=2,则AD为( )
A.2 B.2 C.3 D.2.5
答案:A
6、如图6,经测BE=60m,CE=30m,CD=35m,则河的宽度AB的长为( )
A.30m B.35m C.60m D.70m
答案:D
7、如图7,有两棵树,一棵高10m,另一棵高4m,两树相距8m。一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行( )
A.8m B.10m C.12m D.14m
答案:B
8、如图8所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.a C.2a D.3a
答案:C
二、填空题
9、在某时刻的阳光照耀下,身高160cm的小花的影长为80cm,她身旁的旗杆影长10m,则旗杆高为 m。
答案:20
10、如图9,小军从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小军的身高为1.6米,那么路灯离地面的高度AB是 米。
答案:5.6
11、如图10,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 。
答案:6
12、如图11,某河边一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米。
答案:(5+5)
13、在直角△ABC中,AD是斜边BC上的高,BD=5,CD=9,则AD= 。
答案:3
14、已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 。
答案:9
三、解答题
15、如图,某校在一次数学课外活动中,小李同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向。小李沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向。求教学楼A与办公楼B之间的距离(结果精确到0.1米)(供选用的数据:≈1.414,≈1.732)。
答案:解:由题意可知
∠ACP=∠BCP=90° ∠APC=30° ∠BPC=45°
在Rt△BPC中:
∵ ∠BCP=90° ∠BPC=45°
∴ BC=PC=60m
在Rt△ACP中:
∵ ∠ACP=90° ∠APC=30°
设AC=x 则AP=2x 由勾股定理得:
x2+602=(2x)2 解得:x=20 即:AC=20m
∴ AB=AC+BC=60+20≈60+20×1.732=94.64≈94.6(米)
答:教学楼A与办公楼B之间的距离大约为94.6米。
16、如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm。如果小张瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置。
(1)求证:△BEF∽△CDF;(2)求CF的长。
答案:解:(1)在矩形ABCD中,由对称性可得出:
∠DFC=∠EFB ∠EBF=∠FCD=90°
∴ △BEF∽△CDF
(2)∵ 由(1)知:△BEF∽△CDF
∴ = 即= 解得:CF=169
答:CF的长度是169cm。
17、如图,小军将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,求旗杆的高度(滑轮上方的部分忽略不计)。
答案:解:过点C作CF⊥AD交AD于点F。
设AD=x 则AC=x AF=x-2
在Rt△AFC中:由勾股定理得:
(x-2)2+82=x2 解得:x=17
答:旗杆的高度是17m。
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
华师版秋学期九年级上册数学《测量》专题训练
一、选择题
1、如图1,一场暴风雨过后,垂直于地面的一棵树在距地面2米处折断,树尖B恰好碰到地面,经测量AB=3米,则树高为( )
A.米 B.米 C.(+2)米 D.5米
2、某科技兴趣小组为测量学校旗杆AC的高度,在点F竖立一根长为1.5米的标杆DF,如图2所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影长BC的长度为6米,那么旗杆AC的高度为( )
A.5.5米 B.7米 C.8.5米 D.9米
3、如图3,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上。若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
4、如图4,李四要测量河内小岛B到河边公路的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路的距离为( )米。
A.25 B.25 C. D.25+25
5、如图5,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=6,CD=2,则AD为( )
A.2 B.2 C.3 D.2.5
6、如图6,经测BE=60m,CE=30m,CD=35m,则河的宽度AB的长为( )
A.30m B.35m C.60m D.70m
7、如图7,有两棵树,一棵高10m,另一棵高4m,两树相距8m。一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行( )
A.8m B.10m C.12m D.14m
8、如图8所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.a C.2a D.3a
二、填空题
9、在某时刻的阳光照耀下,身高160cm的小花的影长为80cm,她身旁的旗杆影长10m,则旗杆高为 m。
10、如图9,小军从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小军的身高为1.6米,那么路灯离地面的高度AB是 米。
11、如图10,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 。
12、如图11,某河边一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米。
13、在直角△ABC中,AD是斜边BC上的高,BD=5,CD=9,则AD= 。
14、已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 。
三、解答题
15、如图,某校在一次数学课外活动中,小李同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向。小李沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向。求教学楼A与办公楼B之间的距离(结果精确到0.1米)(供选用的数据:≈1.414,≈1.732)。
16、如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm。如果小张瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置。
(1)求证:△BEF∽△CDF;(2)求CF的长。
17、如图,小军将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,求旗杆的高度(滑轮上方的部分忽略不计)。
华师版秋学期九年级上册数学《测量》专题训练答案
一、选择题
1、如图1,一场暴风雨过后,垂直于地面的一棵树在距地面2米处折断,树尖B恰好碰到地面,经测量AB=3米,则树高为( )
A.米 B.米 C.(+2)米 D.5米
答案:C
2、某科技兴趣小组为测量学校旗杆AC的高度,在点F竖立一根长为1.5米的标杆DF,如图2所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影长BC的长度为6米,那么旗杆AC的高度为( )
A.5.5米 B.7米 C.8.5米 D.9米
答案:D
3、如图3,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上。若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
答案:C
4、如图4,李四要测量河内小岛B到河边公路的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路的距离为( )米。
A.25 B.25 C. D.25+25
答案:B
5、如图5,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=6,CD=2,则AD为( )
A.2 B.2 C.3 D.2.5
答案:A
6、如图6,经测BE=60m,CE=30m,CD=35m,则河的宽度AB的长为( )
A.30m B.35m C.60m D.70m
答案:D
7、如图7,有两棵树,一棵高10m,另一棵高4m,两树相距8m。一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行( )
A.8m B.10m C.12m D.14m
答案:B
8、如图8所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.a C.2a D.3a
答案:C
二、填空题
9、在某时刻的阳光照耀下,身高160cm的小花的影长为80cm,她身旁的旗杆影长10m,则旗杆高为 m。
答案:20
10、如图9,小军从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小军的身高为1.6米,那么路灯离地面的高度AB是 米。
答案:5.6
11、如图10,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 。
答案:6
12、如图11,某河边一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米。
答案:(5+5)
13、在直角△ABC中,AD是斜边BC上的高,BD=5,CD=9,则AD= 。
答案:3
14、已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 。
答案:9
三、解答题
15、如图,某校在一次数学课外活动中,小李同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向。小李沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向。求教学楼A与办公楼B之间的距离(结果精确到0.1米)(供选用的数据:≈1.414,≈1.732)。
答案:解:由题意可知
∠ACP=∠BCP=90° ∠APC=30° ∠BPC=45°
在Rt△BPC中:
∵ ∠BCP=90° ∠BPC=45°
∴ BC=PC=60m
在Rt△ACP中:
∵ ∠ACP=90° ∠APC=30°
设AC=x 则AP=2x 由勾股定理得:
x2+602=(2x)2 解得:x=20 即:AC=20m
∴ AB=AC+BC=60+20≈60+20×1.732=94.64≈94.6(米)
答:教学楼A与办公楼B之间的距离大约为94.6米。
16、如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm。如果小张瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置。
(1)求证:△BEF∽△CDF;(2)求CF的长。
答案:解:(1)在矩形ABCD中,由对称性可得出:
∠DFC=∠EFB ∠EBF=∠FCD=90°
∴ △BEF∽△CDF
(2)∵ 由(1)知:△BEF∽△CDF
∴ = 即= 解得:CF=169
答:CF的长度是169cm。
17、如图,小军将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,求旗杆的高度(滑轮上方的部分忽略不计)。
答案:解:过点C作CF⊥AD交AD于点F。
设AD=x 则AC=x AF=x-2
在Rt△AFC中:由勾股定理得:
(x-2)2+82=x2 解得:x=17
答:旗杆的高度是17m。
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
