高中数学人教A版(2019)选修2 5.1 导数的概念及意义 选择题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)选修2 5.1 导数的概念及意义 选择题专项章节综合练习题(答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1003.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 20:36:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1 导数的概念及意义 选择题专项
一、选择题
1.(2023高二下·宝安期中)某物体的运动路程单位:与时间单位:的关系可用函数表示,则该物体在时的瞬时速度为( )
A. B. C. D.
2.(2023高二下·安徽期中)已知某物体在平面上做变速直线运动,且位移(单位:米)与时间(单位:秒)之间的关系可用函数:表示,则该物体在秒时的瞬时速度为( )
A.米/秒 B.米/秒
C.米/秒 D.米秒
3.(2023高二下·梅州期中)函数在区间上的平均变化率为( )
A.1 B.2 C.7 D.9
4.(2023高二下·苏州期中)设函数,则在处的瞬时变化率为( )
A.-2 B.0 C.1 D.2
5.(2023高二下·洛阳期中)某直线运动的物体从时刻到的位移为,那么为( )
A.从时刻到物体的平均速度
B.从时刻到位移的平均变化率
C.当时刻为时该物体的速度
D.该物体在时刻的瞬时速度
6.(2023高二上·武汉期末)已知函数可导,且满足,则函数在x=3处的导数为( )
A.2 B.1 C.-1 D.-2
7.(2022高三上·金沙期中)现有一个圆柱形空杯子,盛液体部分的底面半径为2cm,高为8cm,用一个注液器向杯中注入溶液,已知注液器向杯中注入的溶液的容积V(单位:ml)关于时间(单位:s)的函数解析式为,不考虑注液过程中溶液的流失,则当时,杯中溶液上升高度的瞬时变化率为( )
A.4 cm/s B.5 cm/s C.6 cm/s D.7cm/s
8.(2022高二下·石家庄期末)向某容器内注入水,已知容器中水的高度h(单位:)与时间t(单位:s)的函数关系式为,则当时,容器中水的高度的瞬时变化率为( )
A. B. C. D.
9.(2022高二下·邢台期末)一个质点的位移s(单位:m)与时间t(单位:s)满足函数关系式,则当时,该质点的瞬时速度为( )
A. B. C. D.
10.(2022高二下·西城期末)函数在处的瞬时变化率为( )
A.-2 B.-4 C.- D.-
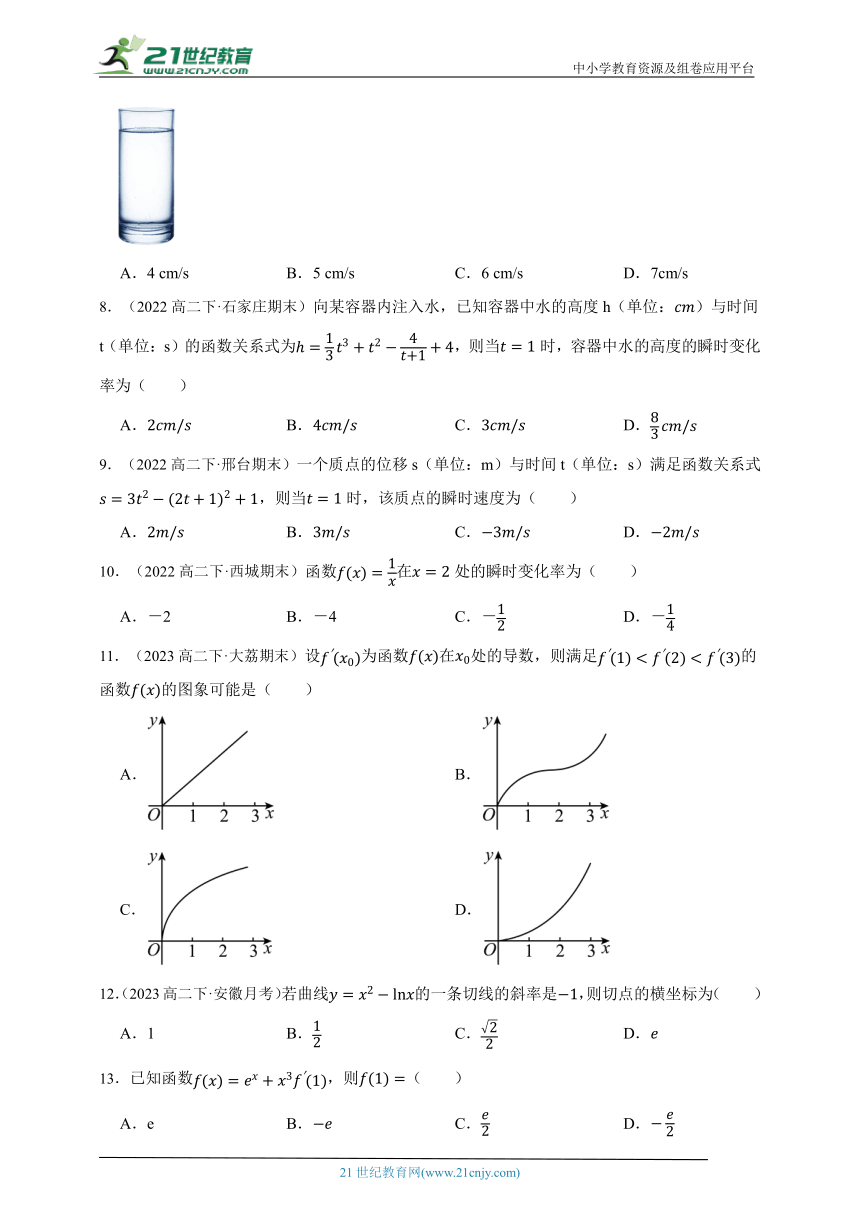
11.(2023高二下·大荔期末)设为函数在处的导数,则满足的函数的图象可能是( )
A. B.
C. D.
12.(2023高二下·安徽月考)若曲线的一条切线的斜率是,则切点的横坐标为( )
A.1 B. C. D.
13.已知函数,则( )
A.e B. C. D.
14.(2023高二下·洛阳期末)若,则( )
A.2 B.1 C. D.-1
15.(2023高二下·百色期末)设f(x)是可导函数,且,则( )
A.2 B. C.-1 D.-2
16.(2022高二下·韩城期末)若函数在处的导数为2,则( )
A.2 B.1 C. D.6
17.(2022高二下·浙江期中)已知函数,若,则( )
A.1 B.2 C.3 D.4
18.(2022高二下·武功期中)一质点在单位圆上作圆周运动,其位移满足的方程为,其中h表示位移(单位:m),t表示时间(单位:s),则该质点在时的瞬时速度为( )
A. B. C. D.
19.(2022高二下·武汉月考)设是定义在R上的可导函数,若(为常数),则( )
A. B. C. D.
20.(2023高二下·成都期中)若函数在点处的切线斜率为1,则( )
A.-e B.e C.-1 D.1
21.(2023高二下·平阳月考)过点作曲线的切线,所得切线斜率为( )
A.-3 B.0或3 C.-3或24 D.0
22.(2023高二下·台州期中)曲线在点处的切线的倾斜角为( )
A. B. C. D.
23.(2023高二下·花都期中)已知函数的图象如图所示,设函数从到的平均变化率为,从到的平均变化率为,则与的大小关系为( )
A. B. C. D.不确定
24.(2023高二下·洛阳期末)曲线在点处的切线方程是( )
A. B.
C. D.
25.(2023高二下·简阳月考)若经过点P(2,8)作曲线 的切线,则切线方程为( )
A. B.
C. 或 D. 或
26.(2023高二下·安徽期中)设,则( )
A.-5 B.-20 C.5 D.20
27.(2023高二下·合肥期中)设在处可导,则( )
A. B. C. D.
28.(2022高二下·邢台月考)已知函数,则( )
A. B. C. D.
29.(2023·诸暨模拟)如图是函数的导函数的图象,若,则的图象大致为( )
A. B.
C. D.
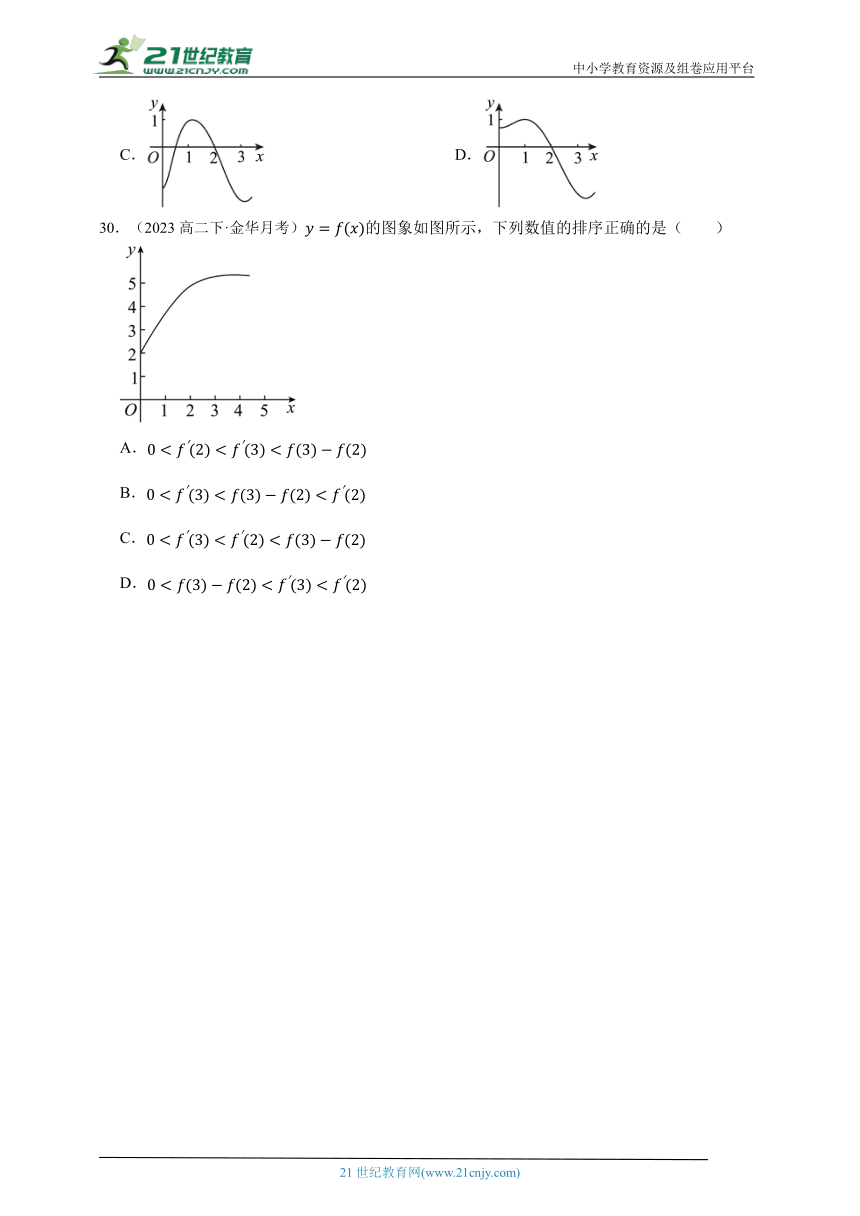
30.(2023高二下·金华月考)的图象如图所示,下列数值的排序正确的是( )
A.
B.
C.
D.
答案解析部分
1.【答案】D
【解析】【解答】由导数的物理意义知路程在某时刻的导数值是物体在该时刻的瞬时速度,
, ,物体在时的瞬时速度为.
故答案为:D
【分析】利用导数的物理意义进行求解。
2.【答案】A
【解析】【解答】由题得,当时,,故瞬时速度为米/秒,
故答案为:A.
【分析】直接对位移关于时间的函数求导,代入求解即可得答案.
3.【答案】C
【解析】【解答】根据平均变化率的定义可知,.
所以函数在区间上的平均变化率为7.
故答案为:C
【分析】根据平均变化率的定义可求出答案.
4.【答案】A
【解析】【解答】,,.
故答案为:A
【分析】 利用导数的运算法则,瞬时变化率的定义求解,即可得答案.
5.【答案】D
【解析】【解答】根据题意,直线运动的物体,从时刻到时,时间的变化量为,而物体的位移为,那么为该物体在时刻的瞬时速度.
故答案为:D.
【分析】利用已知条件结合平均变化率求解方法和函数求极限的方法,从而找出正确的选项。
6.【答案】D
【解析】【解答】由题意,,所以.
故答案为:D.
【分析】根据导数的定义,得到,进而的值.
7.【答案】C
【解析】【解答】由题设,杯子底面积为,则溶液上升高度,
所以,则cm/s.
故答案为:C
【分析】由题设可得溶液上升高度,求导并代入求值即可.
8.【答案】B
【解析】【解答】,当时,,故当时,容器中水的高度的瞬时变化率为.
故答案为:B
【分析】求导,当时,可求出容器中水的高度的瞬时变化率.
9.【答案】C
【解析】【解答】解:因为,所以,
当时,,故当时,该质点的瞬时速度为.
故答案为:C
【分析】 先求质点的运动方程为的导数,再求得秒时的导数,即可得到所求的瞬时速度.
10.【答案】D
【解析】【解答】由题设,故.
故答案为:D
【分析】 函数在x=2处的瞬时变化率为曲线在该点处的导数,计算可得答案.
11.【答案】D
【解析】【解答】由导数的几何意义知表示函数在处切线的斜率,
因为,所以函数分别在处切线的斜率越来越大,由选项可得D正确.
故答案为:D
【分析】本题主要考查导数的几何意义,数形结合可得答案.
12.【答案】B
【解析】【解答】设切点的横坐标为x,则,解得或x=-1(舍去).
故选:B.
【分析】 设出切点横坐标,求导,通过斜率得出横坐标方程,求解可得切点的横坐标 .
13.【答案】C
14.【答案】C
【解析】【解答】解:因为,
所以,
故答案为:C.
【分析】根据题意结合导数的定义运算求解.
15.【答案】B
【解析】【解答】因为 .
故答案为:B.
【分析】根据导数的定义运算求解.
16.【答案】B
【解析】【解答】由函数在处的导数为2,得,
所以。
故答案为:B
【分析】利用已知条件结合导数的定义与极限的关系,进而得出的值。
17.【答案】C
【解析】【解答】由,得,
又因为,所以,
即,解得。
故答案为:C.
【分析】利用已知条件结合函数的极限求解方法和导数的定义,再结合代入法得出实数b的值。
18.【答案】B
【解析】【解答】根据导数的物理意义可知,位移的导数就是瞬时速度,,所以。
故答案为:B
【分析】利用已知条件和导数与瞬时速度的关系式,进而得出该质点在时的瞬时速度。
19.【答案】C
【解析】【解答】.
故答案为:C.
【分析】由导数的定义即可求解。
20.【答案】D
【解析】【解答】因为,
所以在点处的切线斜率为,解得,
故答案为:D.
【分析】根据某点切线斜率与导函数等价关系,求导即可求解出的值.
21.【答案】C
【解析】【解答】由已知可得,点不在曲线上,设切点为
因为,根据导数的几何意义可得,切线斜率,
又切线过点,所以,
所以,整理可得.
又,所以有,
即,解得或.
当时,;当时,.
所以切线斜率为-3或24.
故答案为:C.
【分析】利用已知条件结合导数的几何意义得出曲线的切线的斜率与切点横坐标的关系式,再结合两点求斜率公式和代入法,进而得出切点的横坐标,从而得出切线的斜率。
22.【答案】B
【解析】【解答】因为,所以,,
设线在点处的切线的倾斜角为,
由导数的几何意义知,即.
所以曲线在点处的切线的倾斜角为.
故答案为:B.
【分析】利用已知条件结合导数的几何意义得出切线的斜率,再结合直线的斜率与直线的倾斜角的关系式,进而得出曲线在点处的切线的倾斜角。
23.【答案】C
【解析】【解答】∵,
,
∴
【分析】利用平均变化率公式求解即可.
24.【答案】A
【解析】【解答】解:由题意可得:,则,即切线斜率为,
所以曲线在点处的切线方程是,即,
故答案为:A.
【分析】根据题意结合导数的几何意义运算求解.
25.【答案】D
【解析】【解答】解:①易知P点在曲线上,当P点为切点时,y=3x2,k=12,12x-y-16=0 .
②当P点不是切点时,设切点为A(x0,y0) ,由定义可求得切线的斜率为 .
∵A在曲线上,
∴,
∴,
∴,
∴ ,
解得x0=-1或x0=2(舍去),
∴ y0=-1,k=3,
此时切线方程为y+1=3(x+1),
即3x-y+2=0 .
故经过点P的曲线的切线有两条,方程为12x-y-16=0或3x-y+2=0 .
故选:D
【分析】因为P点在曲线上,所以需要分两种情况讨论,P点为切点和P点不为切点,分别根据导数的几何意义求解切线方程即可.
26.【答案】A
【解析】【解答】,即.
故答案为:A.
【分析】利用已知条件结合导数的定义和函数的极限的关系,进而结合代入法得出导函数的值。
27.【答案】A
【解析】【解答】因为在处可导, 由导数的定义可得:,
所以,.
故答案为:A.
【分析】利用已知条件结合导数的定义和函数的极限的关系,进而得出的值。
28.【答案】A
【解析】【解答】因为,
所以,
所以.
故答案为:A.
【分析】先计算,再结合导数的定义即可求解。
29.【答案】D
【解析】【解答】由f(x)的导函数图象可得,
所以f(x)在(0,1)上单调递增,(1,2)上单调递减,上递增,所以A错误;
由导数值在(0,1)小于1可得f(x)在(0,1)的切线斜率小于1,
所以B,C错误,D正确;
故答案为:D.
【分析】利用导数正负和原函数单调区间的关系,导数值和切线斜率的关系,即可求解.
30.【答案】B
【解析】【解答】
由图可知:,
即.
故答案为:B
【分析】利用已知条件结合导数的几何意义和两点求斜率公式,再结合函数的图象和比较法找出数值排序正确的选项。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1 导数的概念及意义 选择题专项
一、选择题
1.(2023高二下·宝安期中)某物体的运动路程单位:与时间单位:的关系可用函数表示,则该物体在时的瞬时速度为( )
A. B. C. D.
2.(2023高二下·安徽期中)已知某物体在平面上做变速直线运动,且位移(单位:米)与时间(单位:秒)之间的关系可用函数:表示,则该物体在秒时的瞬时速度为( )
A.米/秒 B.米/秒
C.米/秒 D.米秒
3.(2023高二下·梅州期中)函数在区间上的平均变化率为( )
A.1 B.2 C.7 D.9
4.(2023高二下·苏州期中)设函数,则在处的瞬时变化率为( )
A.-2 B.0 C.1 D.2
5.(2023高二下·洛阳期中)某直线运动的物体从时刻到的位移为,那么为( )
A.从时刻到物体的平均速度
B.从时刻到位移的平均变化率
C.当时刻为时该物体的速度
D.该物体在时刻的瞬时速度
6.(2023高二上·武汉期末)已知函数可导,且满足,则函数在x=3处的导数为( )
A.2 B.1 C.-1 D.-2
7.(2022高三上·金沙期中)现有一个圆柱形空杯子,盛液体部分的底面半径为2cm,高为8cm,用一个注液器向杯中注入溶液,已知注液器向杯中注入的溶液的容积V(单位:ml)关于时间(单位:s)的函数解析式为,不考虑注液过程中溶液的流失,则当时,杯中溶液上升高度的瞬时变化率为( )
A.4 cm/s B.5 cm/s C.6 cm/s D.7cm/s
8.(2022高二下·石家庄期末)向某容器内注入水,已知容器中水的高度h(单位:)与时间t(单位:s)的函数关系式为,则当时,容器中水的高度的瞬时变化率为( )
A. B. C. D.
9.(2022高二下·邢台期末)一个质点的位移s(单位:m)与时间t(单位:s)满足函数关系式,则当时,该质点的瞬时速度为( )
A. B. C. D.
10.(2022高二下·西城期末)函数在处的瞬时变化率为( )
A.-2 B.-4 C.- D.-
11.(2023高二下·大荔期末)设为函数在处的导数,则满足的函数的图象可能是( )
A. B.
C. D.
12.(2023高二下·安徽月考)若曲线的一条切线的斜率是,则切点的横坐标为( )
A.1 B. C. D.
13.已知函数,则( )
A.e B. C. D.
14.(2023高二下·洛阳期末)若,则( )
A.2 B.1 C. D.-1
15.(2023高二下·百色期末)设f(x)是可导函数,且,则( )
A.2 B. C.-1 D.-2
16.(2022高二下·韩城期末)若函数在处的导数为2,则( )
A.2 B.1 C. D.6
17.(2022高二下·浙江期中)已知函数,若,则( )
A.1 B.2 C.3 D.4
18.(2022高二下·武功期中)一质点在单位圆上作圆周运动,其位移满足的方程为,其中h表示位移(单位:m),t表示时间(单位:s),则该质点在时的瞬时速度为( )
A. B. C. D.
19.(2022高二下·武汉月考)设是定义在R上的可导函数,若(为常数),则( )
A. B. C. D.
20.(2023高二下·成都期中)若函数在点处的切线斜率为1,则( )
A.-e B.e C.-1 D.1
21.(2023高二下·平阳月考)过点作曲线的切线,所得切线斜率为( )
A.-3 B.0或3 C.-3或24 D.0
22.(2023高二下·台州期中)曲线在点处的切线的倾斜角为( )
A. B. C. D.
23.(2023高二下·花都期中)已知函数的图象如图所示,设函数从到的平均变化率为,从到的平均变化率为,则与的大小关系为( )
A. B. C. D.不确定
24.(2023高二下·洛阳期末)曲线在点处的切线方程是( )
A. B.
C. D.
25.(2023高二下·简阳月考)若经过点P(2,8)作曲线 的切线,则切线方程为( )
A. B.
C. 或 D. 或
26.(2023高二下·安徽期中)设,则( )
A.-5 B.-20 C.5 D.20
27.(2023高二下·合肥期中)设在处可导,则( )
A. B. C. D.
28.(2022高二下·邢台月考)已知函数,则( )
A. B. C. D.
29.(2023·诸暨模拟)如图是函数的导函数的图象,若,则的图象大致为( )
A. B.
C. D.
30.(2023高二下·金华月考)的图象如图所示,下列数值的排序正确的是( )
A.
B.
C.
D.
答案解析部分
1.【答案】D
【解析】【解答】由导数的物理意义知路程在某时刻的导数值是物体在该时刻的瞬时速度,
, ,物体在时的瞬时速度为.
故答案为:D
【分析】利用导数的物理意义进行求解。
2.【答案】A
【解析】【解答】由题得,当时,,故瞬时速度为米/秒,
故答案为:A.
【分析】直接对位移关于时间的函数求导,代入求解即可得答案.
3.【答案】C
【解析】【解答】根据平均变化率的定义可知,.
所以函数在区间上的平均变化率为7.
故答案为:C
【分析】根据平均变化率的定义可求出答案.
4.【答案】A
【解析】【解答】,,.
故答案为:A
【分析】 利用导数的运算法则,瞬时变化率的定义求解,即可得答案.
5.【答案】D
【解析】【解答】根据题意,直线运动的物体,从时刻到时,时间的变化量为,而物体的位移为,那么为该物体在时刻的瞬时速度.
故答案为:D.
【分析】利用已知条件结合平均变化率求解方法和函数求极限的方法,从而找出正确的选项。
6.【答案】D
【解析】【解答】由题意,,所以.
故答案为:D.
【分析】根据导数的定义,得到,进而的值.
7.【答案】C
【解析】【解答】由题设,杯子底面积为,则溶液上升高度,
所以,则cm/s.
故答案为:C
【分析】由题设可得溶液上升高度,求导并代入求值即可.
8.【答案】B
【解析】【解答】,当时,,故当时,容器中水的高度的瞬时变化率为.
故答案为:B
【分析】求导,当时,可求出容器中水的高度的瞬时变化率.
9.【答案】C
【解析】【解答】解:因为,所以,
当时,,故当时,该质点的瞬时速度为.
故答案为:C
【分析】 先求质点的运动方程为的导数,再求得秒时的导数,即可得到所求的瞬时速度.
10.【答案】D
【解析】【解答】由题设,故.
故答案为:D
【分析】 函数在x=2处的瞬时变化率为曲线在该点处的导数,计算可得答案.
11.【答案】D
【解析】【解答】由导数的几何意义知表示函数在处切线的斜率,
因为,所以函数分别在处切线的斜率越来越大,由选项可得D正确.
故答案为:D
【分析】本题主要考查导数的几何意义,数形结合可得答案.
12.【答案】B
【解析】【解答】设切点的横坐标为x,则,解得或x=-1(舍去).
故选:B.
【分析】 设出切点横坐标,求导,通过斜率得出横坐标方程,求解可得切点的横坐标 .
13.【答案】C
14.【答案】C
【解析】【解答】解:因为,
所以,
故答案为:C.
【分析】根据题意结合导数的定义运算求解.
15.【答案】B
【解析】【解答】因为 .
故答案为:B.
【分析】根据导数的定义运算求解.
16.【答案】B
【解析】【解答】由函数在处的导数为2,得,
所以。
故答案为:B
【分析】利用已知条件结合导数的定义与极限的关系,进而得出的值。
17.【答案】C
【解析】【解答】由,得,
又因为,所以,
即,解得。
故答案为:C.
【分析】利用已知条件结合函数的极限求解方法和导数的定义,再结合代入法得出实数b的值。
18.【答案】B
【解析】【解答】根据导数的物理意义可知,位移的导数就是瞬时速度,,所以。
故答案为:B
【分析】利用已知条件和导数与瞬时速度的关系式,进而得出该质点在时的瞬时速度。
19.【答案】C
【解析】【解答】.
故答案为:C.
【分析】由导数的定义即可求解。
20.【答案】D
【解析】【解答】因为,
所以在点处的切线斜率为,解得,
故答案为:D.
【分析】根据某点切线斜率与导函数等价关系,求导即可求解出的值.
21.【答案】C
【解析】【解答】由已知可得,点不在曲线上,设切点为
因为,根据导数的几何意义可得,切线斜率,
又切线过点,所以,
所以,整理可得.
又,所以有,
即,解得或.
当时,;当时,.
所以切线斜率为-3或24.
故答案为:C.
【分析】利用已知条件结合导数的几何意义得出曲线的切线的斜率与切点横坐标的关系式,再结合两点求斜率公式和代入法,进而得出切点的横坐标,从而得出切线的斜率。
22.【答案】B
【解析】【解答】因为,所以,,
设线在点处的切线的倾斜角为,
由导数的几何意义知,即.
所以曲线在点处的切线的倾斜角为.
故答案为:B.
【分析】利用已知条件结合导数的几何意义得出切线的斜率,再结合直线的斜率与直线的倾斜角的关系式,进而得出曲线在点处的切线的倾斜角。
23.【答案】C
【解析】【解答】∵,
,
∴
【分析】利用平均变化率公式求解即可.
24.【答案】A
【解析】【解答】解:由题意可得:,则,即切线斜率为,
所以曲线在点处的切线方程是,即,
故答案为:A.
【分析】根据题意结合导数的几何意义运算求解.
25.【答案】D
【解析】【解答】解:①易知P点在曲线上,当P点为切点时,y=3x2,k=12,12x-y-16=0 .
②当P点不是切点时,设切点为A(x0,y0) ,由定义可求得切线的斜率为 .
∵A在曲线上,
∴,
∴,
∴,
∴ ,
解得x0=-1或x0=2(舍去),
∴ y0=-1,k=3,
此时切线方程为y+1=3(x+1),
即3x-y+2=0 .
故经过点P的曲线的切线有两条,方程为12x-y-16=0或3x-y+2=0 .
故选:D
【分析】因为P点在曲线上,所以需要分两种情况讨论,P点为切点和P点不为切点,分别根据导数的几何意义求解切线方程即可.
26.【答案】A
【解析】【解答】,即.
故答案为:A.
【分析】利用已知条件结合导数的定义和函数的极限的关系,进而结合代入法得出导函数的值。
27.【答案】A
【解析】【解答】因为在处可导, 由导数的定义可得:,
所以,.
故答案为:A.
【分析】利用已知条件结合导数的定义和函数的极限的关系,进而得出的值。
28.【答案】A
【解析】【解答】因为,
所以,
所以.
故答案为:A.
【分析】先计算,再结合导数的定义即可求解。
29.【答案】D
【解析】【解答】由f(x)的导函数图象可得,
所以f(x)在(0,1)上单调递增,(1,2)上单调递减,上递增,所以A错误;
由导数值在(0,1)小于1可得f(x)在(0,1)的切线斜率小于1,
所以B,C错误,D正确;
故答案为:D.
【分析】利用导数正负和原函数单调区间的关系,导数值和切线斜率的关系,即可求解.
30.【答案】B
【解析】【解答】
由图可知:,
即.
故答案为:B
【分析】利用已知条件结合导数的几何意义和两点求斜率公式,再结合函数的图象和比较法找出数值排序正确的选项。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
