高中数学人教A版(2019)选修2 5.2 导数的运算1选择题章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)选修2 5.2 导数的运算1选择题章节综合练习题(答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 00:00:00 | ||
图片预览


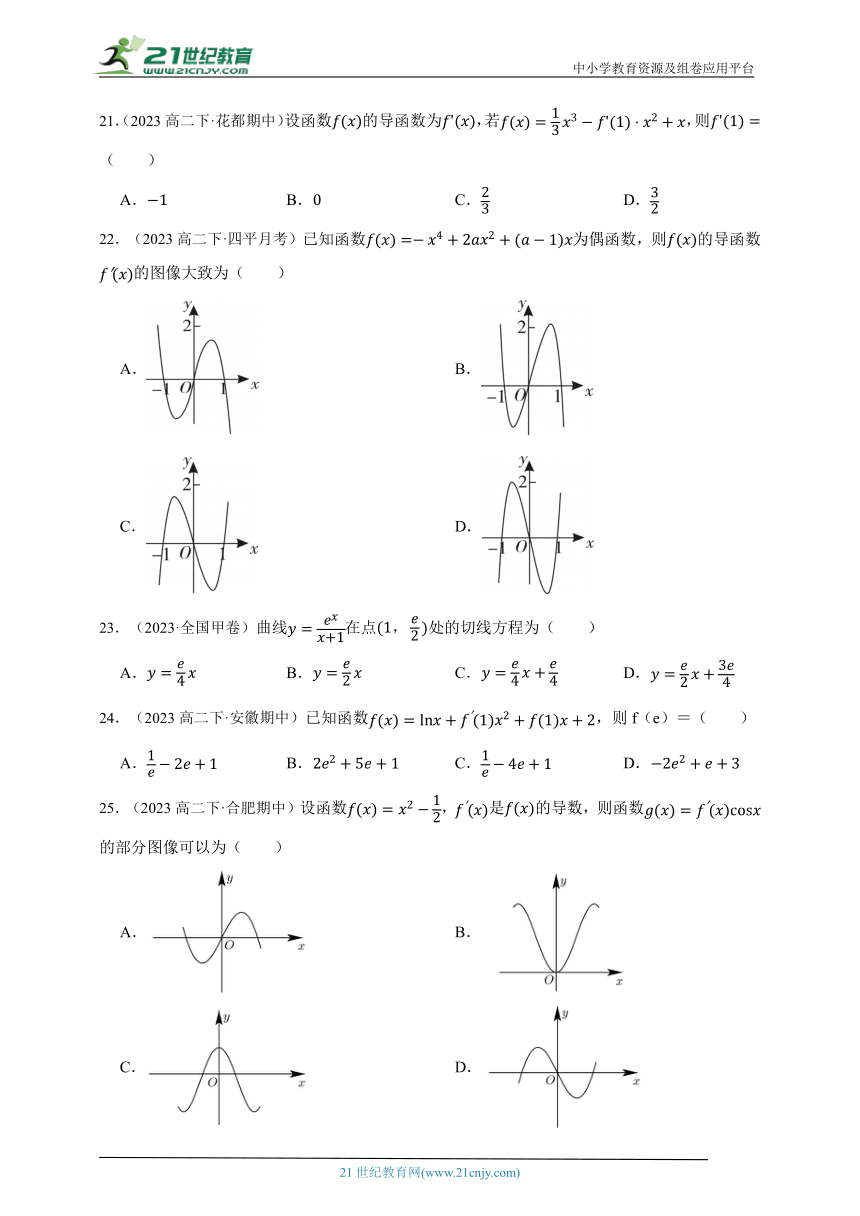


文档简介
中小学教育资源及组卷应用平台
5.2 导数的运算1选择题
一、选择题
1.(2023高二下·清远期末)已知函数,则( )
A. B. C. D.
2.(2023高二下·千阳期中)已知函数在R上可导,且,则与的大小关系是
A. B.
C. D.不确定
3.(2023高二下·成都期中)下列导数运算正确的是( )
A. B.
C. D.
4.(2023高二下·成都期中)函数的导函数为( )
A. B.
C. D.
5.(2023高二下·千阳期中)函数的导数是( )
A. B.
C. D.
6.(2023高二下·安徽期中)设函数,已知,,,,则( )
A.-2 B.-1 C. D.3
7.(2023高二下·河东期中)已知函数,那么的值为( )
A. B. C. D.
8.(2023高二下·南阳期中)若,则( )
A.0 B. C. D.
9.设函数,则( )
A. B. C. D.
10.(2023高二下·郫都期中)函数的导函数等于( )
A. B.
C. D.
11.(2023高二下·大荔期末)函数f(x)=1+sinx,其导函数为f(x),则f()=( )
A. B. C. D.
12.(2023高二下·定远期末)已知函数,则( )
A. B. C. D.
13.(2023高二下·清远期末)已知函数f(x)=ex-2x,则f'(2)=( )
A.e2-4 B.e2-2 C.e2+e D.e2+2
14.(2022高二下·蓝田期末)下列求导错误的是( )
A. B.
C. D.
15.(2022高二下·友好期末)函数的导数为( )
A. B.
C. D.
16.(2022高二下·浙江期中)下列导数运算正确的是( )
A. B.
C. D.
17.(2022高二下·宿州期中)已知函数,若,则( )
A.-1 B. C. D.1
18.(2023高二下·联合期末)下列运算正确的是( )
A. B.
C. D.
19.(2022高二下·韩城期末)已知函数,则( )
A.-π B.0 C.π D.1
20.(2022高二下·玉林期中)函数的导数是( )
A. B.
C. D.
21.(2023高二下·花都期中)设函数的导函数为,若,则( )
A. B. C. D.
22.(2023高二下·四平月考)已知函数为偶函数,则的导函数的图像大致为( )
A. B.
C. D.
23.(2023·全国甲卷)曲线在点处的切线方程为( )
A. B. C. D.
24.(2023高二下·安徽期中)已知函数,则f(e)=( )
A. B. C. D.
25.(2023高二下·合肥期中)设函数,是的导数,则函数的部分图像可以为( )
A. B.
C. D.
26.(2023·湛江模拟)已知函数及其导函数的定义域均为R,且为奇函数,,,则( )
A.13 B.16 C.25 D.51
27.(2023·浙江模拟)若函数满足,,设的导函数为,当时,,则( )
A.65 B.70 C.75 D.80
28.(2023高二下·中山期末)下列求导数计算错误的是( )
A. B.
C. D.
29.(2023高二上·孝义期末)是函数的导函数,则( )
A. B.
C. D.
30.(2023·湖北模拟)函数的导函数为( )
A. B.
C. D.
答案解析部分
1.【答案】B
【解析】【解答】因为 ,所以.
故答案为:B.
【分析】根据导数的运算法则求导,进而求 .
2.【答案】B
【解析】【解答】,
所以,
所以.
故答案为:B
【分析】先求出导函数f'(x),令x=2求出f'(2) , 即可得到f(x) ,把1和-1代入即可比较f(-1)与f(1)的大小关系.
3.【答案】C
【解析】【解答】由,,,,
所以A、B、D不符合题意,C对.
故答案为:C
【分析】 根据基本初等函数、积的导数和复合函数的求导公式对每个选项函数进行求导,即可得答案.
4.【答案】D
【解析】【解答】函数,求导得.
故答案为:D
【分析】利用求导公式计算可得答案.
5.【答案】A
【解析】【解答】令,,,
则,
所以.
故答案为:A
【分析】根据复合函数的导数运算法则求导,可得答案.
6.【答案】B
【解析】【解答】由已知,
.
故答案为:B.
【分析】 先求出函数 的导函数,再代入已知条件计算h'(2)即可得答案.
7.【答案】D
【解析】【解答】,故.
故答案为:D.
【分析】根据导数的公式进行计算,可得答案.
8.【答案】A
【解析】【解答】∵,∴.
故答案为:A.
【分析】利用已知条件结合导数公式得出导数。
9.【答案】B
【解析】【解答】因为,所以,
故,解得
故答案为:B.
【分析】先对函数求导,进而求出 ,代入已知函数解析式中可求出答案.
10.【答案】A
【解析】【解答】由导数的乘法运算法则得
,
故答案为:A.
【分析】根据导数的乘法法则以及复合函数的导数求解,可得答案.
11.【答案】A
【解析】【解答】函数f(x)=1+sinx,其导函数为f′(x)=cosx,∴,
故答案为:A.
【分析】先求出导函数f′(x)=cosx,再代入值可得答案.
12.【答案】A
【解析】【解答】因为 ,则.
故答案为:A.
【分析】根据题意求导,进而代入求值即可.
13.【答案】B
【解析】【解答】由题意可得,所以.
故答案为:B.
【分析】先求函数的导函数,进而可得结果.
14.【答案】B
【解析】【解答】、、运算正确.
,B选项错误.
故答案为:B
【分析】利用已知条件结合导数的运算法则,进而找出求导错误的选项。
15.【答案】B
【解析】【解答】根据导数的运算法则可知,。
故答案为:B
【分析】利用已知条件结合导数的加减法运算法则,进而得出函数的导数。
16.【答案】B
【解析】【解答】对于A,,A不符合题意;
对于B,,B符合题意;
对于C,C不符合题意;
对于D,,D不符合题意.
故答案为:B
【分析】利用导数的加减法运算法则和乘除法运算法则,进而找出导数运算正确的选项。
17.【答案】C
【解析】【解答】因为,所以,又,
所以,解得。
故答案为:C
【分析】利用已知条件结合导数的运算法则得出导函数,再利用代入法得出实数m的值。
18.【答案】C
【解析】【解答】对A:,故A错误;
对B:,故B错误;
对C:,故C正确;
对D:,故D错误.
故答案为:C.
【分析】根据求导运算逐项分析判断即可.
19.【答案】A
【解析】【解答】,所以。
故答案为:A
【分析】利用已知条件结合复合函数的导数运算法则,进而结合代入法得出导函数的值。
20.【答案】C
【解析】【解答】因为函数
所以
故答案为:C.
【分析】因为函数为复合函数,利用复合函数的导数公式求出函数的导数.
21.【答案】C
【解析】【解答】∵,
∴,
∴,
∴,
故选:C.
【分析】根据导数的性质求解即可.
22.【答案】A
【解析】【解答】函数 为偶函数 ,则f(-x)=f(x) ,
即: ,
据此可得:a-1=0 ,a=1
函数的解析式为: ,其导函数 ,
二阶导函数 , f'(x)在递减,在递增,
所以函数 f'(x)的极大值为: ,
观察所给的函数图象,只有A选项符合题意.
故选:A
【分析】首先利用偶函数的性质求得实数a的值,然后求解f'(x)的解析式,二次求导研究导函数的极值,利用极值点即可求得最终结果.
23.【答案】C
【解析】【解答】,
,
即此时该切线方程的斜率为,
曲线在点处的切线方程为,即
故选:C
【分析】利用导数求出在的值,即为点处切线的斜率,由直线点斜式方程得出答案.
24.【答案】D
【解析】【解答】函数,则,解得,
所以,所以,
所以,解得,所以,
所以.
故答案为:D.
【分析】令x=1可得,求出,求导函数可得,结合可求出,进而求出的解析式,代入x=e即可得答案.
25.【答案】A
【解析】【解答】因为,所以,定义域为R,
且,
所以为奇函数,所以排除BC选项,
又,
∴,所以排除D选项,
故答案为:A.
【分析】利用已知条件结合函数的奇偶性,再结合x的取值范围结合函数求值域的方法得出函数 的部分图象。
26.【答案】C
【解析】【解答】由,令,得,所以.
由为奇函数,得,所以,
故①.
又②,
由①和②得,即,
所以,③
令,得,得,
令,得,得.
又④,
由③-④得,即,
所以函数是以8为周期的周期函数,
故,
所以,
所以
,
故答案为:C.
【分析】根据题意推得,得到函数是以8为周期的周期函数,求得,结合周期性,即可求解.
27.【答案】A
【解析】【解答】由,,知函数关于,点对称,
如图,
为向上攀爬的类周期函数,,
由可得,
,
由可得,
,
所以,则有,
所以,
所以,
故答案为:A.
【分析】根据题意得到函数关于点对称,作出函数的图象,结合为向上攀爬的类周期函数,由得到和,再由得到和,得到,进而得到,即可求得的值.
28.【答案】B
【解析】【解答】对A:,故A正确;
对B:,故B错误;
对C:,故C正确;
对D:,故D正确;
故答案为:B.
【分析】根据基本初等函数的导函数结合导数的运算法则逐项分析判断.
29.【答案】A
【解析】【解答】因为,所以,
所以,.
故答案为:A
【分析】先对函数求导,然后求出,判断即可.
30.【答案】D
【解析】【解答】依题知,,即,
由求导公式:,
复合函数的求导法则:设,则
得:,
故答案为:D.
【分析】由求导公式:,再利用复合函数的求导法则可得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.2 导数的运算1选择题
一、选择题
1.(2023高二下·清远期末)已知函数,则( )
A. B. C. D.
2.(2023高二下·千阳期中)已知函数在R上可导,且,则与的大小关系是
A. B.
C. D.不确定
3.(2023高二下·成都期中)下列导数运算正确的是( )
A. B.
C. D.
4.(2023高二下·成都期中)函数的导函数为( )
A. B.
C. D.
5.(2023高二下·千阳期中)函数的导数是( )
A. B.
C. D.
6.(2023高二下·安徽期中)设函数,已知,,,,则( )
A.-2 B.-1 C. D.3
7.(2023高二下·河东期中)已知函数,那么的值为( )
A. B. C. D.
8.(2023高二下·南阳期中)若,则( )
A.0 B. C. D.
9.设函数,则( )
A. B. C. D.
10.(2023高二下·郫都期中)函数的导函数等于( )
A. B.
C. D.
11.(2023高二下·大荔期末)函数f(x)=1+sinx,其导函数为f(x),则f()=( )
A. B. C. D.
12.(2023高二下·定远期末)已知函数,则( )
A. B. C. D.
13.(2023高二下·清远期末)已知函数f(x)=ex-2x,则f'(2)=( )
A.e2-4 B.e2-2 C.e2+e D.e2+2
14.(2022高二下·蓝田期末)下列求导错误的是( )
A. B.
C. D.
15.(2022高二下·友好期末)函数的导数为( )
A. B.
C. D.
16.(2022高二下·浙江期中)下列导数运算正确的是( )
A. B.
C. D.
17.(2022高二下·宿州期中)已知函数,若,则( )
A.-1 B. C. D.1
18.(2023高二下·联合期末)下列运算正确的是( )
A. B.
C. D.
19.(2022高二下·韩城期末)已知函数,则( )
A.-π B.0 C.π D.1
20.(2022高二下·玉林期中)函数的导数是( )
A. B.
C. D.
21.(2023高二下·花都期中)设函数的导函数为,若,则( )
A. B. C. D.
22.(2023高二下·四平月考)已知函数为偶函数,则的导函数的图像大致为( )
A. B.
C. D.
23.(2023·全国甲卷)曲线在点处的切线方程为( )
A. B. C. D.
24.(2023高二下·安徽期中)已知函数,则f(e)=( )
A. B. C. D.
25.(2023高二下·合肥期中)设函数,是的导数,则函数的部分图像可以为( )
A. B.
C. D.
26.(2023·湛江模拟)已知函数及其导函数的定义域均为R,且为奇函数,,,则( )
A.13 B.16 C.25 D.51
27.(2023·浙江模拟)若函数满足,,设的导函数为,当时,,则( )
A.65 B.70 C.75 D.80
28.(2023高二下·中山期末)下列求导数计算错误的是( )
A. B.
C. D.
29.(2023高二上·孝义期末)是函数的导函数,则( )
A. B.
C. D.
30.(2023·湖北模拟)函数的导函数为( )
A. B.
C. D.
答案解析部分
1.【答案】B
【解析】【解答】因为 ,所以.
故答案为:B.
【分析】根据导数的运算法则求导,进而求 .
2.【答案】B
【解析】【解答】,
所以,
所以.
故答案为:B
【分析】先求出导函数f'(x),令x=2求出f'(2) , 即可得到f(x) ,把1和-1代入即可比较f(-1)与f(1)的大小关系.
3.【答案】C
【解析】【解答】由,,,,
所以A、B、D不符合题意,C对.
故答案为:C
【分析】 根据基本初等函数、积的导数和复合函数的求导公式对每个选项函数进行求导,即可得答案.
4.【答案】D
【解析】【解答】函数,求导得.
故答案为:D
【分析】利用求导公式计算可得答案.
5.【答案】A
【解析】【解答】令,,,
则,
所以.
故答案为:A
【分析】根据复合函数的导数运算法则求导,可得答案.
6.【答案】B
【解析】【解答】由已知,
.
故答案为:B.
【分析】 先求出函数 的导函数,再代入已知条件计算h'(2)即可得答案.
7.【答案】D
【解析】【解答】,故.
故答案为:D.
【分析】根据导数的公式进行计算,可得答案.
8.【答案】A
【解析】【解答】∵,∴.
故答案为:A.
【分析】利用已知条件结合导数公式得出导数。
9.【答案】B
【解析】【解答】因为,所以,
故,解得
故答案为:B.
【分析】先对函数求导,进而求出 ,代入已知函数解析式中可求出答案.
10.【答案】A
【解析】【解答】由导数的乘法运算法则得
,
故答案为:A.
【分析】根据导数的乘法法则以及复合函数的导数求解,可得答案.
11.【答案】A
【解析】【解答】函数f(x)=1+sinx,其导函数为f′(x)=cosx,∴,
故答案为:A.
【分析】先求出导函数f′(x)=cosx,再代入值可得答案.
12.【答案】A
【解析】【解答】因为 ,则.
故答案为:A.
【分析】根据题意求导,进而代入求值即可.
13.【答案】B
【解析】【解答】由题意可得,所以.
故答案为:B.
【分析】先求函数的导函数,进而可得结果.
14.【答案】B
【解析】【解答】、、运算正确.
,B选项错误.
故答案为:B
【分析】利用已知条件结合导数的运算法则,进而找出求导错误的选项。
15.【答案】B
【解析】【解答】根据导数的运算法则可知,。
故答案为:B
【分析】利用已知条件结合导数的加减法运算法则,进而得出函数的导数。
16.【答案】B
【解析】【解答】对于A,,A不符合题意;
对于B,,B符合题意;
对于C,C不符合题意;
对于D,,D不符合题意.
故答案为:B
【分析】利用导数的加减法运算法则和乘除法运算法则,进而找出导数运算正确的选项。
17.【答案】C
【解析】【解答】因为,所以,又,
所以,解得。
故答案为:C
【分析】利用已知条件结合导数的运算法则得出导函数,再利用代入法得出实数m的值。
18.【答案】C
【解析】【解答】对A:,故A错误;
对B:,故B错误;
对C:,故C正确;
对D:,故D错误.
故答案为:C.
【分析】根据求导运算逐项分析判断即可.
19.【答案】A
【解析】【解答】,所以。
故答案为:A
【分析】利用已知条件结合复合函数的导数运算法则,进而结合代入法得出导函数的值。
20.【答案】C
【解析】【解答】因为函数
所以
故答案为:C.
【分析】因为函数为复合函数,利用复合函数的导数公式求出函数的导数.
21.【答案】C
【解析】【解答】∵,
∴,
∴,
∴,
故选:C.
【分析】根据导数的性质求解即可.
22.【答案】A
【解析】【解答】函数 为偶函数 ,则f(-x)=f(x) ,
即: ,
据此可得:a-1=0 ,a=1
函数的解析式为: ,其导函数 ,
二阶导函数 , f'(x)在递减,在递增,
所以函数 f'(x)的极大值为: ,
观察所给的函数图象,只有A选项符合题意.
故选:A
【分析】首先利用偶函数的性质求得实数a的值,然后求解f'(x)的解析式,二次求导研究导函数的极值,利用极值点即可求得最终结果.
23.【答案】C
【解析】【解答】,
,
即此时该切线方程的斜率为,
曲线在点处的切线方程为,即
故选:C
【分析】利用导数求出在的值,即为点处切线的斜率,由直线点斜式方程得出答案.
24.【答案】D
【解析】【解答】函数,则,解得,
所以,所以,
所以,解得,所以,
所以.
故答案为:D.
【分析】令x=1可得,求出,求导函数可得,结合可求出,进而求出的解析式,代入x=e即可得答案.
25.【答案】A
【解析】【解答】因为,所以,定义域为R,
且,
所以为奇函数,所以排除BC选项,
又,
∴,所以排除D选项,
故答案为:A.
【分析】利用已知条件结合函数的奇偶性,再结合x的取值范围结合函数求值域的方法得出函数 的部分图象。
26.【答案】C
【解析】【解答】由,令,得,所以.
由为奇函数,得,所以,
故①.
又②,
由①和②得,即,
所以,③
令,得,得,
令,得,得.
又④,
由③-④得,即,
所以函数是以8为周期的周期函数,
故,
所以,
所以
,
故答案为:C.
【分析】根据题意推得,得到函数是以8为周期的周期函数,求得,结合周期性,即可求解.
27.【答案】A
【解析】【解答】由,,知函数关于,点对称,
如图,
为向上攀爬的类周期函数,,
由可得,
,
由可得,
,
所以,则有,
所以,
所以,
故答案为:A.
【分析】根据题意得到函数关于点对称,作出函数的图象,结合为向上攀爬的类周期函数,由得到和,再由得到和,得到,进而得到,即可求得的值.
28.【答案】B
【解析】【解答】对A:,故A正确;
对B:,故B错误;
对C:,故C正确;
对D:,故D正确;
故答案为:B.
【分析】根据基本初等函数的导函数结合导数的运算法则逐项分析判断.
29.【答案】A
【解析】【解答】因为,所以,
所以,.
故答案为:A
【分析】先对函数求导,然后求出,判断即可.
30.【答案】D
【解析】【解答】依题知,,即,
由求导公式:,
复合函数的求导法则:设,则
得:,
故答案为:D.
【分析】由求导公式:,再利用复合函数的求导法则可得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
