第22章二次函数综合复习卷(含答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第22章二次函数综合复习卷(含答案)2023-2024学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 08:18:23 | ||
图片预览


文档简介
第22章二次函数 综合复习卷
一.选择题(共12小题)
1.下列函数中,是二次函数的有( )
①;
②;
③y=3x(1﹣3x);
④y=(1﹣2x)(1+2x).
A.1个 B.2个 C.3个 D.4个
2.某工厂的大门是抛物线型水泥建筑物,大门地面宽为8m,两侧距地面3m处各有一个壁灯,两壁灯之间的水平距离为6m,则大门的高约为( )
A.6.9m B.7.0m C.7.1m D.6.8m
3.某种药品售价为每盒300元,经过医保局连续两次“灵魂砍价”,药品企业同意降价若干进入国家医保用药目录.如果每次降价的百分率都是x,则两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是( )
A.y=300(1﹣x) B.y=300(1﹣x)2
C.y=300(1+x) D.y=300(1+x)2
4.抛物线y=x2+2x+a﹣2与坐标轴有且仅有两个交点,则a的值为( )
A.3 B.2 C.2或﹣3 D.2或3
5.“抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )
A.w=(99﹣x)[200+10(x﹣50)]
B.w=(x﹣50)[200+10(99﹣x)]
C.w=(x﹣50)(200+×10)
D.w=(x﹣50)(200+×10)
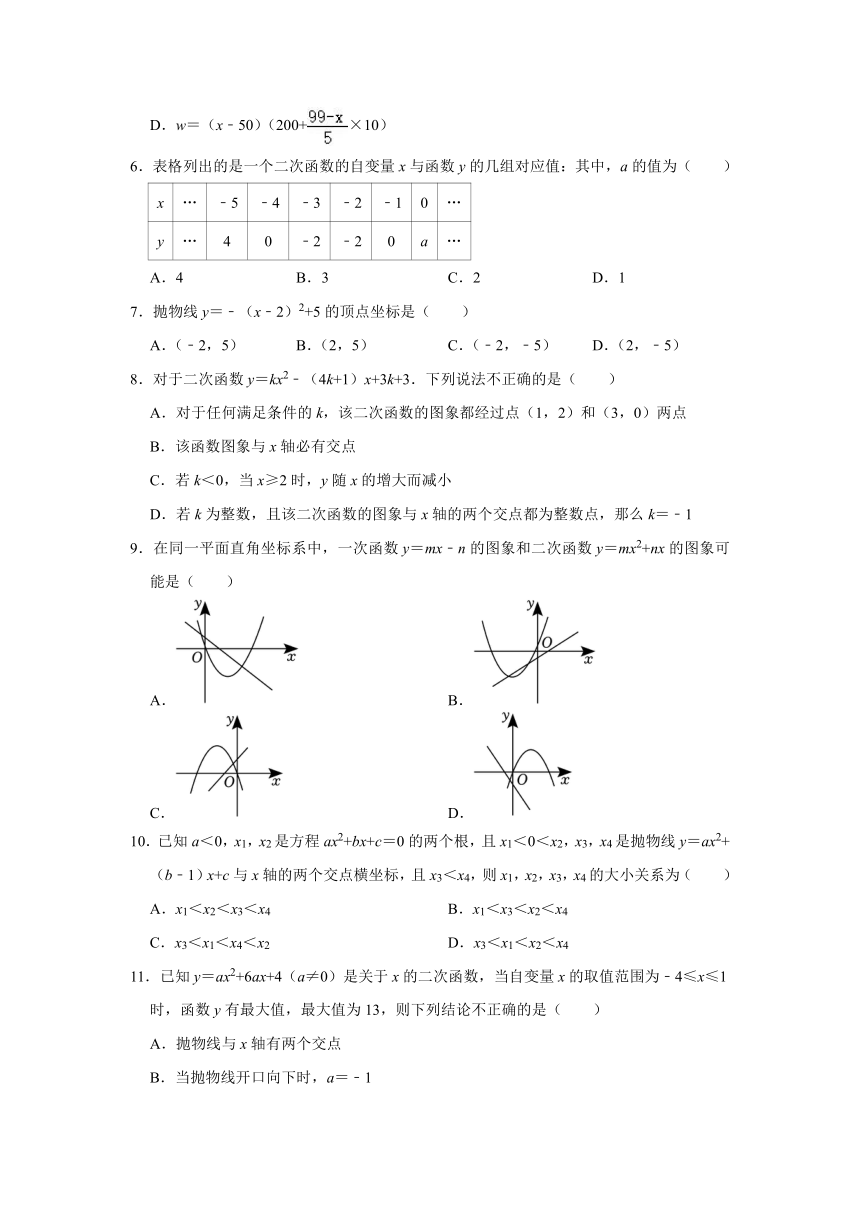
6.表格列出的是一个二次函数的自变量x与函数y的几组对应值:其中,a的值为( )
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 …
y … 4 0 ﹣2 ﹣2 0 a …
A.4 B.3 C.2 D.1
7.抛物线y=﹣(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
8.对于二次函数y=kx2﹣(4k+1)x+3k+3.下列说法不正确的是( )
A.对于任何满足条件的k,该二次函数的图象都经过点(1,2)和(3,0)两点
B.该函数图象与x轴必有交点
C.若k<0,当x≥2时,y随x的增大而减小
D.若k为整数,且该二次函数的图象与x轴的两个交点都为整数点,那么k=﹣1
9.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
10.已知a<0,x1,x2是方程ax2+bx+c=0的两个根,且x1<0<x2,x3,x4是抛物线y=ax2+(b﹣1)x+c与x轴的两个交点横坐标,且x3<x4,则x1,x2,x3,x4的大小关系为( )
A.x1<x2<x3<x4 B.x1<x3<x2<x4
C.x3<x1<x4<x2 D.x3<x1<x2<x4
11.已知y=ax2+6ax+4(a≠0)是关于x的二次函数,当自变量x的取值范围为﹣4≤x≤1时,函数y有最大值,最大值为13,则下列结论不正确的是( )
A.抛物线与x轴有两个交点
B.当抛物线开口向下时,a=﹣1
C.对称轴在y轴的左侧
D.当抛物线开口向上时,
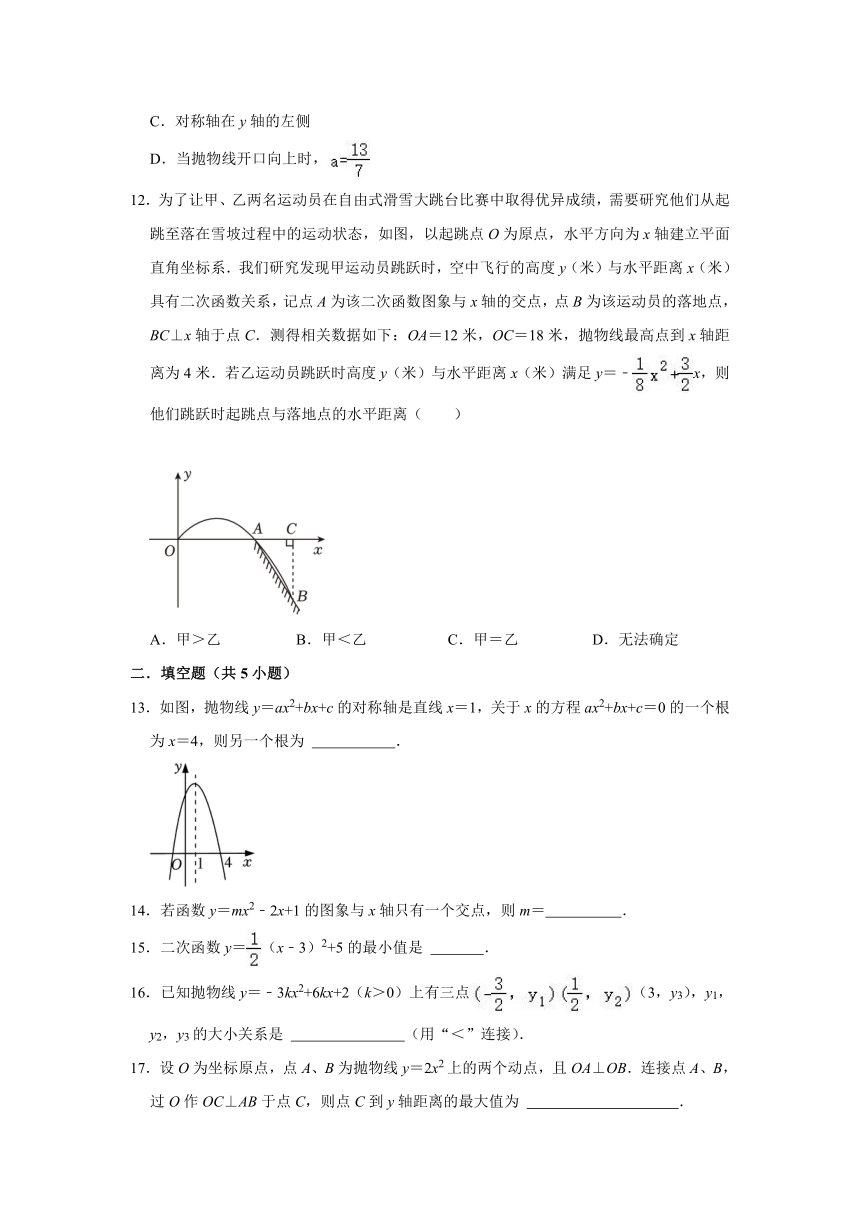
12.为了让甲、乙两名运动员在自由式滑雪大跳台比赛中取得优异成绩,需要研究他们从起跳至落在雪坡过程中的运动状态,如图,以起跳点O为原点,水平方向为x轴建立平面直角坐标系.我们研究发现甲运动员跳跃时,空中飞行的高度y(米)与水平距离x(米)具有二次函数关系,记点A为该二次函数图象与x轴的交点,点B为该运动员的落地点,BC⊥x轴于点C.测得相关数据如下:OA=12米,OC=18米,抛物线最高点到x轴距离为4米.若乙运动员跳跃时高度y(米)与水平距离x(米)满足y=﹣x,则他们跳跃时起跳点与落地点的水平距离( )
A.甲>乙 B.甲<乙 C.甲=乙 D.无法确定
二.填空题(共5小题)
13.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,关于x的方程ax2+bx+c=0的一个根为x=4,则另一个根为 .
14.若函数y=mx2﹣2x+1的图象与x轴只有一个交点,则m= .
15.二次函数y=(x﹣3)2+5的最小值是 .
16.已知抛物线y=﹣3kx2+6kx+2(k>0)上有三点(3,y3),y1,y2,y3的大小关系是 (用“<”连接).
17.设O为坐标原点,点A、B为抛物线y=2x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值为 .
三.解答题(共5小题)
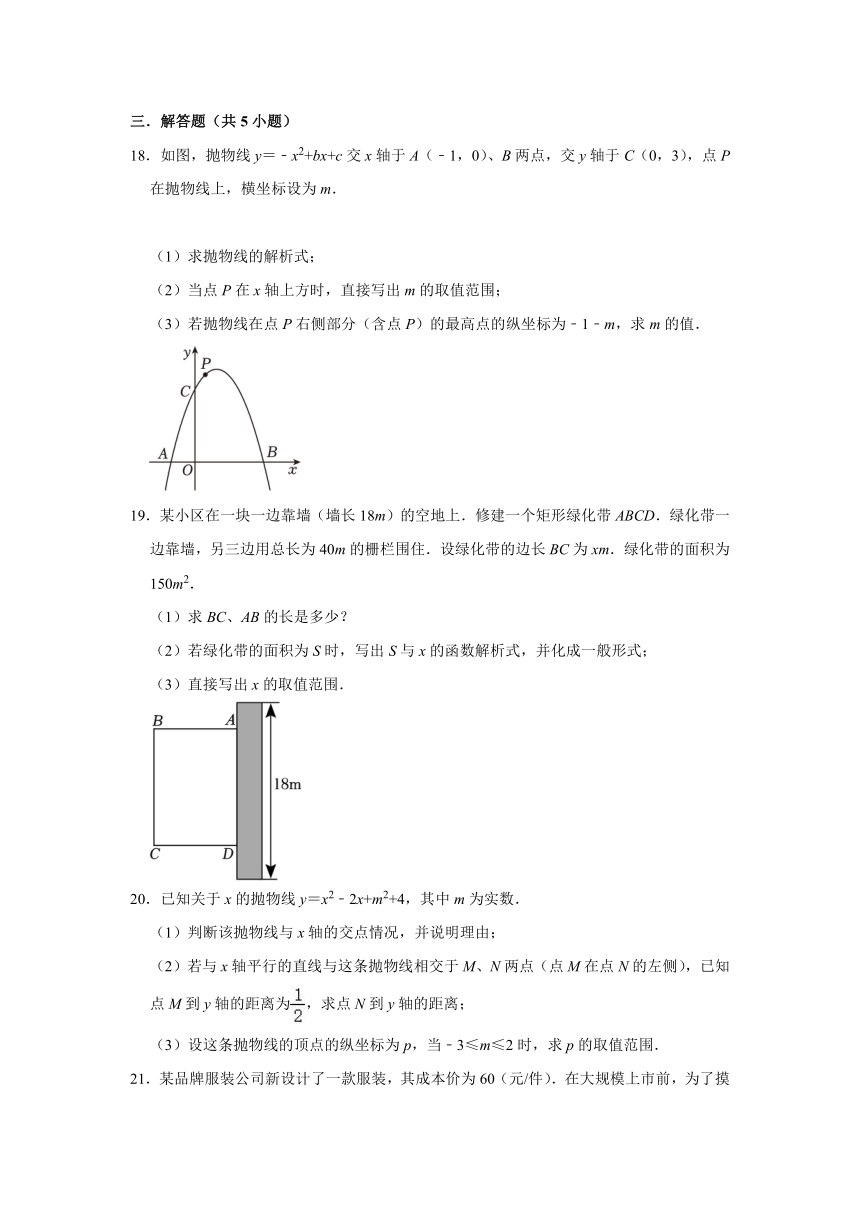
18.如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于C(0,3),点P在抛物线上,横坐标设为m.
(1)求抛物线的解析式;
(2)当点P在x轴上方时,直接写出m的取值范围;
(3)若抛物线在点P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m,求m的值.
19.某小区在一块一边靠墙(墙长18m)的空地上.修建一个矩形绿化带ABCD.绿化带一边靠墙,另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm.绿化带的面积为150m2.
(1)求BC、AB的长是多少?
(2)若绿化带的面积为S时,写出S与x的函数解析式,并化成一般形式;
(3)直接写出x的取值范围.
20.已知关于x的抛物线y=x2﹣2x+m2+4,其中m为实数.
(1)判断该抛物线与x轴的交点情况,并说明理由;
(2)若与x轴平行的直线与这条抛物线相交于M、N两点(点M在点N的左侧),已知点M到y轴的距离为,求点N到y轴的距离;
(3)设这条抛物线的顶点的纵坐标为p,当﹣3≤m≤2时,求p的取值范围.
21.某品牌服装公司新设计了一款服装,其成本价为60(元/件).在大规模上市前,为了摸清款式受欢迎状况以及日销售量y(件)与销售价格x(元/件)之间的关系,进行了市场调查,部分信息如表:
销售价格x(元/件) 80 90 100 110
日销售量y(件) 240 220 200 180
(1)若y与x之间满足一次函数关系,请直接写出函数的解析式 (不用写自变量x的取值范围);
(2)若该公司想每天获利8000元,并尽可能让利给顾客,则应如何定价?
(3)为了帮助贫困山区的小朋友,公司决定每卖出一件服装向希望小学捐款10元,该公司应该如何定价,才能使每天获利最大?(利润用w表示)
22.如图,在平面直角坐标系中,抛物线交x轴于A(﹣3,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的表达式;
(2)直线与直线BC交于点E.点M(m,0)是线段AB上的动点,过点M作x轴的垂线,交直线AE于点G,交抛物线于点F,交直线BC于点H.
①若点F在第二象限,且,求m的值;
②在平面内是否存在点P,使得以点E、F、H、P为顶点的四边形是正方形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案
一.选择题(共12小题)
1--10CABDD ABDDC 11--12DA
二.填空题(共5小题)
13.x=﹣2
14.0或1
15.5
16.y1<y3<y2
17.
三.解答题(共5小题)
18.解:(1)由题意,将A、C两点坐标代入已知解析式得,,
∴.
∴所求解析式为:y=﹣x2+2x+3.
(2)由题意,抛物线交x轴于A、B两点,
又解析式为y=﹣x2+2x+3,A(﹣1,0),
∴令y=0,有﹣x2+2x+3=0,又一个根是﹣1.
∴根据两根之积为﹣3,从而可以求得B(3,0).
∴结合图象,当点P在x轴上方时,﹣1<m<3.
(3)由题意,y=﹣x2+2x+3的对称轴为x=1.
当m≤1时,当x=1时,P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m=4,
∴m=﹣5.
当m>1时,当x=m时,P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m=﹣m2+2m+3,
∴m1=﹣1(舍去),m2=4.
综上,符合题意得m为﹣5或4.
19.解:(1)∵边长BC为xm.
∴AB=(40﹣x)=20﹣x,
根据题意得x(20﹣x)=150,
解得x1=10,x2=30(不合题意舍去),
答:BC的长是10m,AB的长是15m;
(2)根据题意得S=x(20﹣x),
即S=﹣x2+20x;
(3)∵墙长18m
∴x的取值范围为0<x≤18.
20.解:(1)抛物线与x轴没有交点.
令y=0,得x2﹣2x+m2+4=0,
因为(﹣2)2﹣4(m2+4)=﹣4m2﹣12<0,
所以这条抛物线与x轴没有交点;
(2)因为y=x2﹣2x+m2+4=(x﹣1)2+m2+3,
所以抛物线的对称轴为x=1.
又与x轴平行的直线与这条抛物线相交于M、N两点(点M在点N的左侧),
所以M、N关于x=1对称,
因为点M到y轴的距离为,
所以M的横坐标为或.
当点M的横坐标为时,点N的横坐标为;
当点M的横坐标为时,点N的横坐标为;
所以点N到y轴的距离为.
(3)∵y=x2﹣2x+m2+4=(x﹣1)2+m2+3,
∴顶点的纵坐标为m2+3,即p=m2+3.
对于二次函数p=m2+3,当﹣3≤m<0,p随m的增大而减小,
∴当m=﹣3时,p取最大值12;
当0<m≤2,p随m的增大而增大,即当m=2时,p取最大值7.
又m=0时,p取得最小值3.
∴当﹣3≤m≤2时,p的取值范围为3≤p≤12.
21.解:设(1)y与x之间的函数关系式为y=kx+b,
则,
解得,
∴y与x之间的函数关系式为y=﹣2x+400,
故答案为:y=﹣2x+400;
(2)根据题意得:(x﹣60)(﹣2x+400)=8000,
解得x1=100,x2=160,
∵公司尽可能多让利给顾客,
∴应定价100元;
(3)根据题意得w=(x﹣60﹣10)(﹣2x+400)=﹣2x2+540x﹣28000=﹣2(x﹣135)2+8450,
∵﹣2<0,
∴当x=135时,w有最大值,最大值为8450,
答:当一件衣服定为135元时,才能使每天获利最大.
22.解:(1)∵抛物线y=﹣x2+bx+c交x轴于A(﹣3,0),B(4,0)两点,
∴y=﹣(x+3)(x﹣4)=﹣;
(2)①如图1,
∵B(4,0),C(0,4),
∴设BC的解析式为:y=kx+n,
则,
解得,
∴BC的解析式为:y=﹣x+4,
∴﹣x+4=,
解得:x=1,
∴E(1,3),
∵M(m,0),且MH⊥x轴,
∴G(m,),F(m,﹣),
∵S△EFG=S△OEG,
∴=×ON(xE﹣xG),
[(﹣)﹣()](1﹣m)=×(1﹣m),
解得:m1=﹣1,m2=﹣;
②存在,由①知:E(1,3),
∵四边形EFHP是正方形,
∴FH=EF,∠EFH=∠FHP=∠HPE=∠90°,
∵M(m,0),且MH⊥x轴,
∴H(m,﹣m+4),F(m,﹣),
分两种情况:
i)当﹣3≤m<1时,如图2,点F在EP的左侧,
∴FH=(﹣m+4)﹣(﹣)=,
∵EF=FH,
∴,
解得:m1=(舍),m2=,
∴H(,),
∴P(1,),
ii)当1<m<4时,点F在PE的右边,如图3,
同理得﹣=m﹣1,
解得:m1=,m2=(舍),
同理得P(1,);
综上,点P的坐标为:或
一.选择题(共12小题)
1.下列函数中,是二次函数的有( )
①;
②;
③y=3x(1﹣3x);
④y=(1﹣2x)(1+2x).
A.1个 B.2个 C.3个 D.4个
2.某工厂的大门是抛物线型水泥建筑物,大门地面宽为8m,两侧距地面3m处各有一个壁灯,两壁灯之间的水平距离为6m,则大门的高约为( )
A.6.9m B.7.0m C.7.1m D.6.8m
3.某种药品售价为每盒300元,经过医保局连续两次“灵魂砍价”,药品企业同意降价若干进入国家医保用药目录.如果每次降价的百分率都是x,则两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是( )
A.y=300(1﹣x) B.y=300(1﹣x)2
C.y=300(1+x) D.y=300(1+x)2
4.抛物线y=x2+2x+a﹣2与坐标轴有且仅有两个交点,则a的值为( )
A.3 B.2 C.2或﹣3 D.2或3
5.“抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )
A.w=(99﹣x)[200+10(x﹣50)]
B.w=(x﹣50)[200+10(99﹣x)]
C.w=(x﹣50)(200+×10)
D.w=(x﹣50)(200+×10)
6.表格列出的是一个二次函数的自变量x与函数y的几组对应值:其中,a的值为( )
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 …
y … 4 0 ﹣2 ﹣2 0 a …
A.4 B.3 C.2 D.1
7.抛物线y=﹣(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
8.对于二次函数y=kx2﹣(4k+1)x+3k+3.下列说法不正确的是( )
A.对于任何满足条件的k,该二次函数的图象都经过点(1,2)和(3,0)两点
B.该函数图象与x轴必有交点
C.若k<0,当x≥2时,y随x的增大而减小
D.若k为整数,且该二次函数的图象与x轴的两个交点都为整数点,那么k=﹣1
9.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
10.已知a<0,x1,x2是方程ax2+bx+c=0的两个根,且x1<0<x2,x3,x4是抛物线y=ax2+(b﹣1)x+c与x轴的两个交点横坐标,且x3<x4,则x1,x2,x3,x4的大小关系为( )
A.x1<x2<x3<x4 B.x1<x3<x2<x4
C.x3<x1<x4<x2 D.x3<x1<x2<x4
11.已知y=ax2+6ax+4(a≠0)是关于x的二次函数,当自变量x的取值范围为﹣4≤x≤1时,函数y有最大值,最大值为13,则下列结论不正确的是( )
A.抛物线与x轴有两个交点
B.当抛物线开口向下时,a=﹣1
C.对称轴在y轴的左侧
D.当抛物线开口向上时,
12.为了让甲、乙两名运动员在自由式滑雪大跳台比赛中取得优异成绩,需要研究他们从起跳至落在雪坡过程中的运动状态,如图,以起跳点O为原点,水平方向为x轴建立平面直角坐标系.我们研究发现甲运动员跳跃时,空中飞行的高度y(米)与水平距离x(米)具有二次函数关系,记点A为该二次函数图象与x轴的交点,点B为该运动员的落地点,BC⊥x轴于点C.测得相关数据如下:OA=12米,OC=18米,抛物线最高点到x轴距离为4米.若乙运动员跳跃时高度y(米)与水平距离x(米)满足y=﹣x,则他们跳跃时起跳点与落地点的水平距离( )
A.甲>乙 B.甲<乙 C.甲=乙 D.无法确定
二.填空题(共5小题)
13.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,关于x的方程ax2+bx+c=0的一个根为x=4,则另一个根为 .
14.若函数y=mx2﹣2x+1的图象与x轴只有一个交点,则m= .
15.二次函数y=(x﹣3)2+5的最小值是 .
16.已知抛物线y=﹣3kx2+6kx+2(k>0)上有三点(3,y3),y1,y2,y3的大小关系是 (用“<”连接).
17.设O为坐标原点,点A、B为抛物线y=2x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值为 .
三.解答题(共5小题)
18.如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于C(0,3),点P在抛物线上,横坐标设为m.
(1)求抛物线的解析式;
(2)当点P在x轴上方时,直接写出m的取值范围;
(3)若抛物线在点P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m,求m的值.
19.某小区在一块一边靠墙(墙长18m)的空地上.修建一个矩形绿化带ABCD.绿化带一边靠墙,另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm.绿化带的面积为150m2.
(1)求BC、AB的长是多少?
(2)若绿化带的面积为S时,写出S与x的函数解析式,并化成一般形式;
(3)直接写出x的取值范围.
20.已知关于x的抛物线y=x2﹣2x+m2+4,其中m为实数.
(1)判断该抛物线与x轴的交点情况,并说明理由;
(2)若与x轴平行的直线与这条抛物线相交于M、N两点(点M在点N的左侧),已知点M到y轴的距离为,求点N到y轴的距离;
(3)设这条抛物线的顶点的纵坐标为p,当﹣3≤m≤2时,求p的取值范围.
21.某品牌服装公司新设计了一款服装,其成本价为60(元/件).在大规模上市前,为了摸清款式受欢迎状况以及日销售量y(件)与销售价格x(元/件)之间的关系,进行了市场调查,部分信息如表:
销售价格x(元/件) 80 90 100 110
日销售量y(件) 240 220 200 180
(1)若y与x之间满足一次函数关系,请直接写出函数的解析式 (不用写自变量x的取值范围);
(2)若该公司想每天获利8000元,并尽可能让利给顾客,则应如何定价?
(3)为了帮助贫困山区的小朋友,公司决定每卖出一件服装向希望小学捐款10元,该公司应该如何定价,才能使每天获利最大?(利润用w表示)
22.如图,在平面直角坐标系中,抛物线交x轴于A(﹣3,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的表达式;
(2)直线与直线BC交于点E.点M(m,0)是线段AB上的动点,过点M作x轴的垂线,交直线AE于点G,交抛物线于点F,交直线BC于点H.
①若点F在第二象限,且,求m的值;
②在平面内是否存在点P,使得以点E、F、H、P为顶点的四边形是正方形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案
一.选择题(共12小题)
1--10CABDD ABDDC 11--12DA
二.填空题(共5小题)
13.x=﹣2
14.0或1
15.5
16.y1<y3<y2
17.
三.解答题(共5小题)
18.解:(1)由题意,将A、C两点坐标代入已知解析式得,,
∴.
∴所求解析式为:y=﹣x2+2x+3.
(2)由题意,抛物线交x轴于A、B两点,
又解析式为y=﹣x2+2x+3,A(﹣1,0),
∴令y=0,有﹣x2+2x+3=0,又一个根是﹣1.
∴根据两根之积为﹣3,从而可以求得B(3,0).
∴结合图象,当点P在x轴上方时,﹣1<m<3.
(3)由题意,y=﹣x2+2x+3的对称轴为x=1.
当m≤1时,当x=1时,P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m=4,
∴m=﹣5.
当m>1时,当x=m时,P右侧部分(含点P)的最高点的纵坐标为﹣1﹣m=﹣m2+2m+3,
∴m1=﹣1(舍去),m2=4.
综上,符合题意得m为﹣5或4.
19.解:(1)∵边长BC为xm.
∴AB=(40﹣x)=20﹣x,
根据题意得x(20﹣x)=150,
解得x1=10,x2=30(不合题意舍去),
答:BC的长是10m,AB的长是15m;
(2)根据题意得S=x(20﹣x),
即S=﹣x2+20x;
(3)∵墙长18m
∴x的取值范围为0<x≤18.
20.解:(1)抛物线与x轴没有交点.
令y=0,得x2﹣2x+m2+4=0,
因为(﹣2)2﹣4(m2+4)=﹣4m2﹣12<0,
所以这条抛物线与x轴没有交点;
(2)因为y=x2﹣2x+m2+4=(x﹣1)2+m2+3,
所以抛物线的对称轴为x=1.
又与x轴平行的直线与这条抛物线相交于M、N两点(点M在点N的左侧),
所以M、N关于x=1对称,
因为点M到y轴的距离为,
所以M的横坐标为或.
当点M的横坐标为时,点N的横坐标为;
当点M的横坐标为时,点N的横坐标为;
所以点N到y轴的距离为.
(3)∵y=x2﹣2x+m2+4=(x﹣1)2+m2+3,
∴顶点的纵坐标为m2+3,即p=m2+3.
对于二次函数p=m2+3,当﹣3≤m<0,p随m的增大而减小,
∴当m=﹣3时,p取最大值12;
当0<m≤2,p随m的增大而增大,即当m=2时,p取最大值7.
又m=0时,p取得最小值3.
∴当﹣3≤m≤2时,p的取值范围为3≤p≤12.
21.解:设(1)y与x之间的函数关系式为y=kx+b,
则,
解得,
∴y与x之间的函数关系式为y=﹣2x+400,
故答案为:y=﹣2x+400;
(2)根据题意得:(x﹣60)(﹣2x+400)=8000,
解得x1=100,x2=160,
∵公司尽可能多让利给顾客,
∴应定价100元;
(3)根据题意得w=(x﹣60﹣10)(﹣2x+400)=﹣2x2+540x﹣28000=﹣2(x﹣135)2+8450,
∵﹣2<0,
∴当x=135时,w有最大值,最大值为8450,
答:当一件衣服定为135元时,才能使每天获利最大.
22.解:(1)∵抛物线y=﹣x2+bx+c交x轴于A(﹣3,0),B(4,0)两点,
∴y=﹣(x+3)(x﹣4)=﹣;
(2)①如图1,
∵B(4,0),C(0,4),
∴设BC的解析式为:y=kx+n,
则,
解得,
∴BC的解析式为:y=﹣x+4,
∴﹣x+4=,
解得:x=1,
∴E(1,3),
∵M(m,0),且MH⊥x轴,
∴G(m,),F(m,﹣),
∵S△EFG=S△OEG,
∴=×ON(xE﹣xG),
[(﹣)﹣()](1﹣m)=×(1﹣m),
解得:m1=﹣1,m2=﹣;
②存在,由①知:E(1,3),
∵四边形EFHP是正方形,
∴FH=EF,∠EFH=∠FHP=∠HPE=∠90°,
∵M(m,0),且MH⊥x轴,
∴H(m,﹣m+4),F(m,﹣),
分两种情况:
i)当﹣3≤m<1时,如图2,点F在EP的左侧,
∴FH=(﹣m+4)﹣(﹣)=,
∵EF=FH,
∴,
解得:m1=(舍),m2=,
∴H(,),
∴P(1,),
ii)当1<m<4时,点F在PE的右边,如图3,
同理得﹣=m﹣1,
解得:m1=,m2=(舍),
同理得P(1,);
综上,点P的坐标为:或
同课章节目录
