08年北京名师高考辅导
图片预览








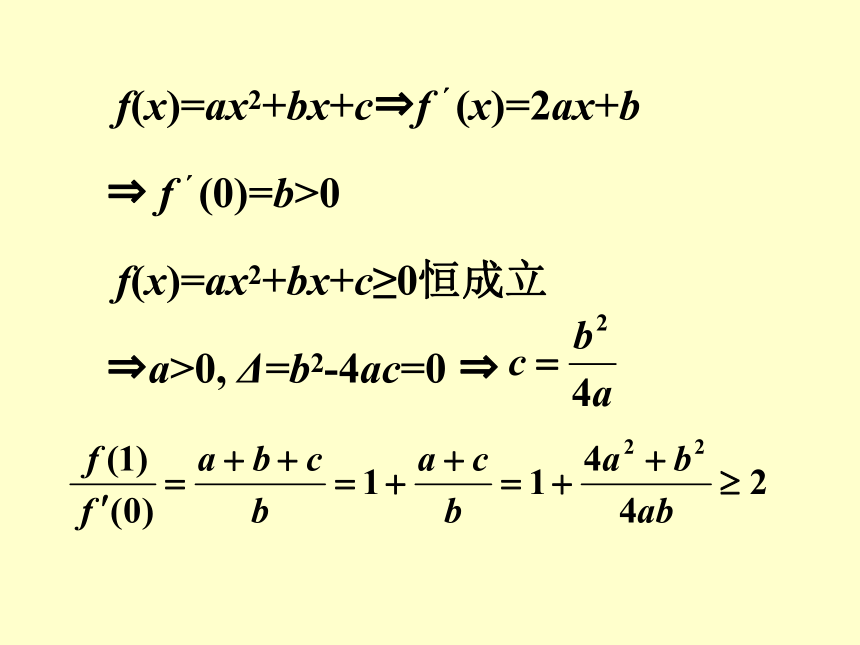



文档简介
课件120张PPT。稳中求变
变中求新 2008.3.17 北京 基本情况
与命题趋势 1. 2007年数学高考的主要特点可以概括为:稳定,过渡,创新. 在实施统一考试,分省命题的第四年,稳定成为十分显著的基本形势,高考的命题更加趋向科学、规范、充实和成熟. 随着实施高中新课程标准的数学教学的省、市和自治区范围逐步扩大,思考并实践数学高考向课程标准卷的过渡,必然成为近几年高考命题关注的热点. 在不断积累经验,相互学习借鉴的过程中,命题力求有所创新,又成为努力追求的目标之一. 2. 稳定,过渡,创新也是2008年数学高考的基本趋势,因此,深入研究高考,明确复习方向,实施科学备考,提高复习效率,应当成为新一轮复习备考的基本方针. 一. 增强综合性,在知识网络交汇点设计试题 对数学知识的考查,既要全面又突出重点. 注重学科的内在联系和知识的综合性,从学科的整体高度和思维价值的高度考虑问题,在知识网络的交汇点设计试题,使对数学知识的考查达到必要的深度.
1.?函数与导数、
方程、不等式 例1 已知二次函数f(x)=ax2+bx+c的导数为f ' (x), f '(0) >0,对于任意实数x,有f(x)≥0,则 的最小值为 A.3 B. C.2 D. f(x)=ax2+bx+c?f ′(x)=2ax+b ? f ′(0)=b>0 f(x)=ax2+bx+c≥0恒成立 ?a>0, Δ=b2-4ac=0 ? 例2 设函数f(x)=ex-e-x. (1) 证明: f(x)的导数f ‘(x)≥2; (2) 若对所有x≥0 ,都有 f(x)≥ax,求a的取值范围. (1) f(x)的导数 f ′(x)=ex+e-x≥2.(当且仅当x=0时,等号成立).
(2) 令g(x)=f(x)-ax,则g ′(x)= f ′(x)-a ,
①若a≤2,当x>0时,g ′(x)= ex+e-x-a≥2-a≥0 ,g(x)在(0,+∞)为增函数,g(x) ≥ g(0),f(x) ≥ ax . ②若a>2,方程g ′(x)=0的正根为 ,
若x?(0,x1),则g ′(x)<0,g(x)在该区间为减函数.
所以,x?(0,x1)时,g(x) < g(0),即f(x) < ax ,与题设f(x) ≥ ax相矛盾. 综上,满足条件的的取值范围是(- ∞ ,2].
2. 数列与函数、
不等式 例3 若数列{an}的前n项和Sn=n2-10n,则此数列的通项公式为an= ;数列{nan}中数值最小的项是第 项. 例4 设数列{an}的首项a1 ∈(0,1), ,…. (1) 求{an}的通项公式; (2) 设 ,证明 bn?BC=
例6 设函数f(x)=a·b,其中向量 a=(m,cos2x),b=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 . (1) 求实数m的值; (2) 求函数f(x)的最小值及此时x值的集合. (1) 由f(x)=a·b=m(1+sin2x)+cos2x, 由已知 ,得m=1. (2) 由(1)得 f(x)=1+sin2x+cos2x 当 时,f(x)的最小值为 x值的集合为{x| Z} . 4. 空间图形 与平面图形 例7 在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 . ① 矩形; ② 不是矩形的平行四边形; ③ 有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④ 每个面都是等边三角形的四面体; ⑤ 每个面都是直角三角形的四面体. 例8如图,在Rt△AOB中, ∠ AOB =30°, 斜边AB=4. Rt△AOC 可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D的斜边AB上. (1) 求证:平面COD⊥平面AOB ; (2) 当D为AB的中点时,求异 面直线AO与CD所成角的大小; (3) 求CD与平面AOB所成角的 最大值. (1) CO⊥平面AOB ; (2) 作DE⊥OB于E,连结CE, 则DE//AO, ∠CDE就是AO 与CD 所成的角 (3) ∠CDO是CD与平面AOB 所成的角,tan ∠CDO OD(OD⊥ AB)最小, ∠CDO最大.5. 解析几何 与函数、向量 例9 设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若 ,则 A.9 B.6 C.4 D.3 例10 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r, 计划将此钢板切割成等腰 梯形的形状,下底AB是半 椭圆的短轴,上底CD的端 点在椭圆上,记CD=2x,梯形面积为S. (1) 求面积S以x为自变量的函数式,并写出其定义域; (2) 求面积S的最大值. (1) 设点C(x,y),则 定义域为{x|00 D.对任意的x∈R,x3-x2+1>0 3.量化突出 数学试题中定量性占有较大的比重. 要把概念、法则、性质寓于计算之中,在运算中考查对算理、运算法则的理解程度、灵活运用的能力及准确严谨的科学态度. 例19 下列四个数中最大的 A.(ln2)2 B.ln(ln2) C. D.ln2 0s1>s2 B. s2>s1>s3 C. s1>s2>s3 D. s2>s3>s1 例44 在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表: (1) 在答题卡上完成频率分
布表,并在给定的坐标系中画
出频率分布直方图; (2) 估计纤度落在中的概率
及纤度小于1.40的概率是多少? (3) 统计方法中,同一组数
据常用该组区间的中点值(例如区间的中点值是1.32)作为代表.据此,估计纤度的期望. 6. 应用意识:主要采用应用问题的形式,主要过程是依据现实的生活背景、提炼相关的数量关系,将实际问题转化为数学问题,构造数学模型,并加以解决.要求考生能理解对问题陈述的材料,并对所提供的信息资料进行归纳、整理和分类,将实际问题抽象为数学问题;应用相关的数学方法解决问题并加以验证,能用数学语言正确地表达和说明. 应用问题的命制坚持“贴近生活,背景公平,控制难度”的原则,切合中学数学教学的实际,应用问题的难度符合考生的水平。 例45 测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得 ,
并在点C 测得塔顶A的
仰角为θ,求塔高AB. 在△BDC中, 在△ABC中, 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 方向300 km的海面P处,并以
20 km/h的速度向西偏北45°
方向移动.台风侵袭的范围为
圆形区域,当前半径为60 km,
并以10 km/h的速度不断增大,
问几小时后该城市开始受到台风的侵袭? 例46 某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元. (1) 求3位购买该商品的顾客中至少有1位采用一次性付款的概率; (2) 求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率. 7.创新意识:高层次的理性思维的考查,在考试中创设新颖的问题情境,构造有一定深度和广度的数学问题;注重问题的多样化,体现思维的发散性;设计反映数、形运动变化的试题,探究型和开放型的试题.要求考生通过“观察、猜测、抽象、概括、推理、证明”等思维程序,发现问题、提出问题,并综合与灵活运用数学知识和思想方法,选择有效的途径和方法,独立思考,探索研究,寻找解决问题的思路,并创造性地解决问题. 例47 设集合S={A0,A1,A2,A3},在S上定义运算⊕为: Ai ⊕Aj=Ak,其中k为i+j被4除的余数,则满足关系式
(x ⊕ x) ⊕ A2= A0的x(x?S)的个数为 A.4 B.3 C.2 D.1 例48 要在边长为16米的正方形草坪上安装喷水龙头,
使整个草坪都能喷洒
到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是 A.3 B.4 C.5 D.6 例49 函数
的最小值为 A. 190 B. 171
C. 90 D. 45 例50 平面α的斜线AB交于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是 A. 一条直线 B. 一个圆 C. 一个椭圆 D. 双曲线的一支
谢 谢
例6 设函数f(x)=a·b,其中向量 a=(m,cos2x),b=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 . (1) 求实数m的值; (2) 求函数f(x)的最小值及此时x值的集合. (1) 由f(x)=a·b=m(1+sin2x)+cos2x, 由已知 ,得m=1. (2) 由(1)得 f(x)=1+sin2x+cos2x 当 时,f(x)的最小值为 x值的集合为{x| Z} . 4. 空间图形 与平面图形 例7 在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 . ① 矩形; ② 不是矩形的平行四边形; ③ 有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④ 每个面都是等边三角形的四面体; ⑤ 每个面都是直角三角形的四面体. 例8如图,在Rt△AOB中, ∠ AOB =30°, 斜边AB=4. Rt△AOC 可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D的斜边AB上. (1) 求证:平面COD⊥平面AOB ; (2) 当D为AB的中点时,求异 面直线AO与CD所成角的大小; (3) 求CD与平面AOB所成角的 最大值. (1) CO⊥平面AOB ; (2) 作DE⊥OB于E,连结CE, 则DE//AO, ∠CDE就是AO 与CD 所成的角 (3) ∠CDO是CD与平面AOB 所成的角,tan ∠CDO OD(OD⊥ AB)最小, ∠CDO最大.5. 解析几何 与函数、向量 例9 设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若 ,则 A.9 B.6 C.4 D.3 例10 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r, 计划将此钢板切割成等腰 梯形的形状,下底AB是半 椭圆的短轴,上底CD的端 点在椭圆上,记CD=2x,梯形面积为S. (1) 求面积S以x为自变量的函数式,并写出其定义域; (2) 求面积S的最大值. (1) 设点C(x,y),则 定义域为{x|0
同课章节目录
