第21章 一元二次方程基础复习卷(二)(21.3)(含答案)
文档属性
| 名称 | 第21章 一元二次方程基础复习卷(二)(21.3)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 442.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 17:55:40 | ||
图片预览


文档简介
第二十一章 一元二次方程基础复习卷(二)(21.3)
知识点一 平均增长(降低)率问题
1.某家快递公司,今年8月份与 10月份完成投递的快递总件数分别为6万件和8.5万件,设该快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是 ( )
A.6(1+x)=8.5 B.6(1+2x)=8.5
2.某商品经过连续两次降价,售价由原来的每件25 元降到每件16元,则平均每次降价的百分率为 ( )
A.20% B.40% C.18% D.36%
3.某工厂一月份生产机器100台,计划二、三月份共生产机器240台,设二、三月份的平均增长率为x,则根据题意列出方程是 ( )
B.100(1+x)+100(1+x) =240
C.100+100(1+x)+100(1+x) =240
4.随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到 2020年底,全省 5G基站数量是目前的4倍;到2022年底,全省5G基站数量将达到 17.34万座.
(1)计划到 2020年底,全省5G基站的数量是多少万座
中小学教育资源及组卷应用平台
(2)按照计划,求2020年底至 2022年底,全省5G基站数量的年平均增长率。
知识点二 几何图形面积问题
5.直角三角形两条直角边的和为7,面积是 6,则斜边长是 ( )
B.5 D.7
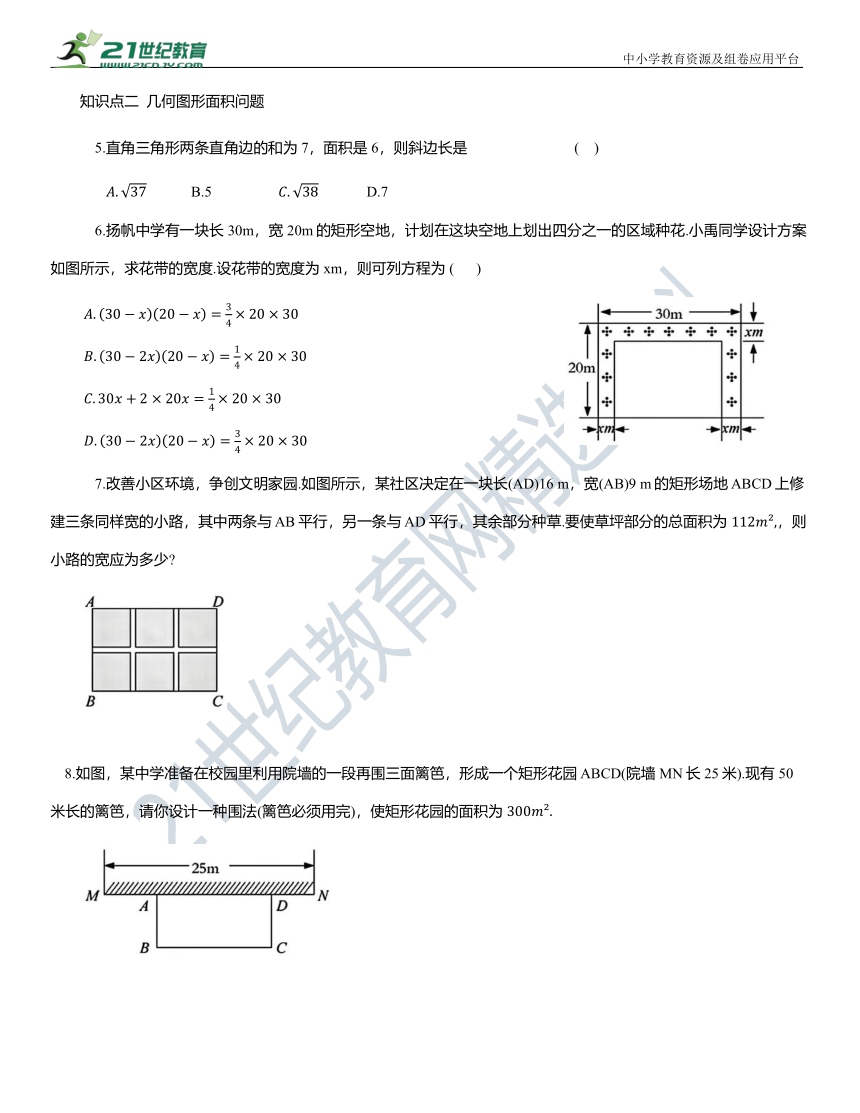
6.扬帆中学有一块长 30m,宽 20m的矩形空地,计划在这块空地上划出四分之一的区域种花.小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为 ( )
7.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16 m,宽(AB)9 m的矩形场地 ABCD上修建三条同样宽的小路,其中两条与 AB平行,另一条与 AD平行,其余部分种草.要使草坪部分的总面积为 ,则小路的宽应为多少
8.如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园 ABCD(院墙MN长25米).现有 50 米长的篱笆,请你设计一种围法(篱笆必须用完),使矩形花园的面积为
9.如图,要建一个面积为 的仓库,仓库的一边靠墙(墙长16m),并在与墙平行的一边开一道 1m 的门,现有能围成32m长的木板,求仓库的长和宽.
10.某地计划对矩形广场进行扩建改造.如图,原广场长 50m,宽 40 m,要求扩充后的矩形广场长与宽的比为3∶2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米 100元.如果计划总费用642 000元,扩充后广场的长和宽应分别是多少米
知识点三 利润问题
11.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出 300个;若销售单价每降低 1元,每天可多售出5个.已知每个电子产品的固定成本为 100元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利32000元
12.一家水果店以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是多少斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,且保证每天至少售出260斤,那么水果店需将每斤的售价降低多少元
13.某水果批发商场经销一种水果,若每千克盈利5元,则每天可售出200千克.经市场调查发现,在进价不变的情况下,若每千克涨价1元,则销售量将减少 10千克.现该商场要保证每天盈利1500元,同时又要顾客得到实惠,则每千克应涨价多少元
知识点四 握手问题及数字问题
14.工会组织篮球比赛庆五一,赛制为单循环形式(每两队之间都赛一场),共进行了 45 场比赛,则这次参加比赛的球队个数为 ( )
A.12个 B.11个 C.9个 D.10个
15.参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了10份合同,则参加商品交易会的公司有 家.
16.已知三个连续奇数的平方和是 371,求这三个奇数.若设中间的奇数是x,则可以列方程为 .
17.一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为 736,求原来的两位数.
1. C 2. A 3. B
4.解:(1)1.5×4=6(万座).
答:到 2020年底,全省 5G基站的数量是6万座.
(2)设全省 5G基站数量的年平均增长率为x,则 解得 (舍去).
答:2020年底至 2022年底,全省 5G基站数量的年平均增长率为 70%.
5. B 6. D
7.解:设小路的宽应为xm,
根据题意可列方程:(16-2x)(9-x)=112,解得
∵16>9,∴x=16不符合题意,舍去,∴x=1.
答:小路的宽应为 l m.
8.解:设AB为x m,则 BC为(50-2x) m,
根据题意得x( 50-2x)=300,
整理得 解得
当 时,50-2x=30>25(不合题意,舍去),当 时,50-2x=20<25(符合题意).
答:当篱笆宽为 15米,长为20米时,花园面积为 300 m .
9.解:设仓库的宽为 xm,则仓库的长为(33-2x)m.
根据题意,得x(33-2x)=130.解得
经检验,x=10和x=6.5均是原方程的根.
当x=10时,33-2x=13;当x=6.5时,33-2x=20.
因为墙长 16 m,所以x=6.5不符合题意,应舍去.
所以仓库的长为 13 m,宽为 10 m.
10.解:设扩充后广场的长为 3x m,宽为 2xm.
根据题意,得3x·2x·100+30(3x·2x-50×40)=642 000.
解得 (不合题意,舍去).所以3x=90,2x=60.
答:扩充后广场的长和宽应分别为 90 m 和60 m.
11.解:设降价后的销售单位为 x 元,则降价后每天可售出[300+5(200-x)]个,
依题意,得:(x-100)[300+5(200-x)]=32000,解得
因为 180<200,所以 符合题意.
故这种电子产品降价后的销售单价为 180元时,公司每天可获利 32000元.
12.解:(1)将这种水果每斤的售价降低x元,
则每天的销售量是 (斤);
(2)根据题意得:(4-2-x)(100+200x)=300,解得:
当 时,销售量是 (斤);
当x=1时,销售量是 100+200=300(斤).
∵每天至少售出260斤,∴x=1.
答:水果店需将每斤的售价降低 1元.
13.解:设每千克应涨价x元.根据题意,得(5+x)(200-10x)=1500,解得 因为顾客要得到实惠,所以x=5.
答:每千克应涨价 5元.
17.解:设原来的两位数十位上的数字为x,则个位上的数字为5-x,依题意得(10x+5-x)[10(5-x)+x]=736,解这个方程得 当x=2时,5-x=3,当x=3时,5-x=2,∴原来的两位数是23 或32.
知识点一 平均增长(降低)率问题
1.某家快递公司,今年8月份与 10月份完成投递的快递总件数分别为6万件和8.5万件,设该快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是 ( )
A.6(1+x)=8.5 B.6(1+2x)=8.5
2.某商品经过连续两次降价,售价由原来的每件25 元降到每件16元,则平均每次降价的百分率为 ( )
A.20% B.40% C.18% D.36%
3.某工厂一月份生产机器100台,计划二、三月份共生产机器240台,设二、三月份的平均增长率为x,则根据题意列出方程是 ( )
B.100(1+x)+100(1+x) =240
C.100+100(1+x)+100(1+x) =240
4.随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到 2020年底,全省 5G基站数量是目前的4倍;到2022年底,全省5G基站数量将达到 17.34万座.
(1)计划到 2020年底,全省5G基站的数量是多少万座
中小学教育资源及组卷应用平台
(2)按照计划,求2020年底至 2022年底,全省5G基站数量的年平均增长率。
知识点二 几何图形面积问题
5.直角三角形两条直角边的和为7,面积是 6,则斜边长是 ( )
B.5 D.7
6.扬帆中学有一块长 30m,宽 20m的矩形空地,计划在这块空地上划出四分之一的区域种花.小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为 ( )
7.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16 m,宽(AB)9 m的矩形场地 ABCD上修建三条同样宽的小路,其中两条与 AB平行,另一条与 AD平行,其余部分种草.要使草坪部分的总面积为 ,则小路的宽应为多少
8.如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园 ABCD(院墙MN长25米).现有 50 米长的篱笆,请你设计一种围法(篱笆必须用完),使矩形花园的面积为
9.如图,要建一个面积为 的仓库,仓库的一边靠墙(墙长16m),并在与墙平行的一边开一道 1m 的门,现有能围成32m长的木板,求仓库的长和宽.
10.某地计划对矩形广场进行扩建改造.如图,原广场长 50m,宽 40 m,要求扩充后的矩形广场长与宽的比为3∶2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米 100元.如果计划总费用642 000元,扩充后广场的长和宽应分别是多少米
知识点三 利润问题
11.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出 300个;若销售单价每降低 1元,每天可多售出5个.已知每个电子产品的固定成本为 100元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利32000元
12.一家水果店以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是多少斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,且保证每天至少售出260斤,那么水果店需将每斤的售价降低多少元
13.某水果批发商场经销一种水果,若每千克盈利5元,则每天可售出200千克.经市场调查发现,在进价不变的情况下,若每千克涨价1元,则销售量将减少 10千克.现该商场要保证每天盈利1500元,同时又要顾客得到实惠,则每千克应涨价多少元
知识点四 握手问题及数字问题
14.工会组织篮球比赛庆五一,赛制为单循环形式(每两队之间都赛一场),共进行了 45 场比赛,则这次参加比赛的球队个数为 ( )
A.12个 B.11个 C.9个 D.10个
15.参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了10份合同,则参加商品交易会的公司有 家.
16.已知三个连续奇数的平方和是 371,求这三个奇数.若设中间的奇数是x,则可以列方程为 .
17.一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为 736,求原来的两位数.
1. C 2. A 3. B
4.解:(1)1.5×4=6(万座).
答:到 2020年底,全省 5G基站的数量是6万座.
(2)设全省 5G基站数量的年平均增长率为x,则 解得 (舍去).
答:2020年底至 2022年底,全省 5G基站数量的年平均增长率为 70%.
5. B 6. D
7.解:设小路的宽应为xm,
根据题意可列方程:(16-2x)(9-x)=112,解得
∵16>9,∴x=16不符合题意,舍去,∴x=1.
答:小路的宽应为 l m.
8.解:设AB为x m,则 BC为(50-2x) m,
根据题意得x( 50-2x)=300,
整理得 解得
当 时,50-2x=30>25(不合题意,舍去),当 时,50-2x=20<25(符合题意).
答:当篱笆宽为 15米,长为20米时,花园面积为 300 m .
9.解:设仓库的宽为 xm,则仓库的长为(33-2x)m.
根据题意,得x(33-2x)=130.解得
经检验,x=10和x=6.5均是原方程的根.
当x=10时,33-2x=13;当x=6.5时,33-2x=20.
因为墙长 16 m,所以x=6.5不符合题意,应舍去.
所以仓库的长为 13 m,宽为 10 m.
10.解:设扩充后广场的长为 3x m,宽为 2xm.
根据题意,得3x·2x·100+30(3x·2x-50×40)=642 000.
解得 (不合题意,舍去).所以3x=90,2x=60.
答:扩充后广场的长和宽应分别为 90 m 和60 m.
11.解:设降价后的销售单位为 x 元,则降价后每天可售出[300+5(200-x)]个,
依题意,得:(x-100)[300+5(200-x)]=32000,解得
因为 180<200,所以 符合题意.
故这种电子产品降价后的销售单价为 180元时,公司每天可获利 32000元.
12.解:(1)将这种水果每斤的售价降低x元,
则每天的销售量是 (斤);
(2)根据题意得:(4-2-x)(100+200x)=300,解得:
当 时,销售量是 (斤);
当x=1时,销售量是 100+200=300(斤).
∵每天至少售出260斤,∴x=1.
答:水果店需将每斤的售价降低 1元.
13.解:设每千克应涨价x元.根据题意,得(5+x)(200-10x)=1500,解得 因为顾客要得到实惠,所以x=5.
答:每千克应涨价 5元.
17.解:设原来的两位数十位上的数字为x,则个位上的数字为5-x,依题意得(10x+5-x)[10(5-x)+x]=736,解这个方程得 当x=2时,5-x=3,当x=3时,5-x=2,∴原来的两位数是23 或32.
同课章节目录
