第二十二章 二次函数综合测试卷(含答案)
文档属性
| 名称 | 第二十二章 二次函数综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 647.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 20:54:51 | ||
图片预览


文档简介
第二十二章 二次函数综合测试卷
(时间:100 分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列是二次函数的是 ( )
B. y=2x+1
2.将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线解析式为( )
3.已知抛物线 经过(-2,n)和(4,n)两点,则n的值为 ( )
A.-2 B. -4 C.2 D.4
4.已知二次函数 关于该函数在-1≤x≤3的取值范围内,下列说法正确的是 ( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值―2
5.如图,二次函数 的图象经过点A(1,0),B(5,0),下列说法正确的是 ( )
A. c<0
C. a-b+c<0
D.图象的对称轴是直线x=3
6.若二次函数 的图象过不同的五点A(m,n),B(0,y ),C(3-m,n),D( ,y ),E(2,y ),!,则 y ,y ,y 的大小关系是 ( )
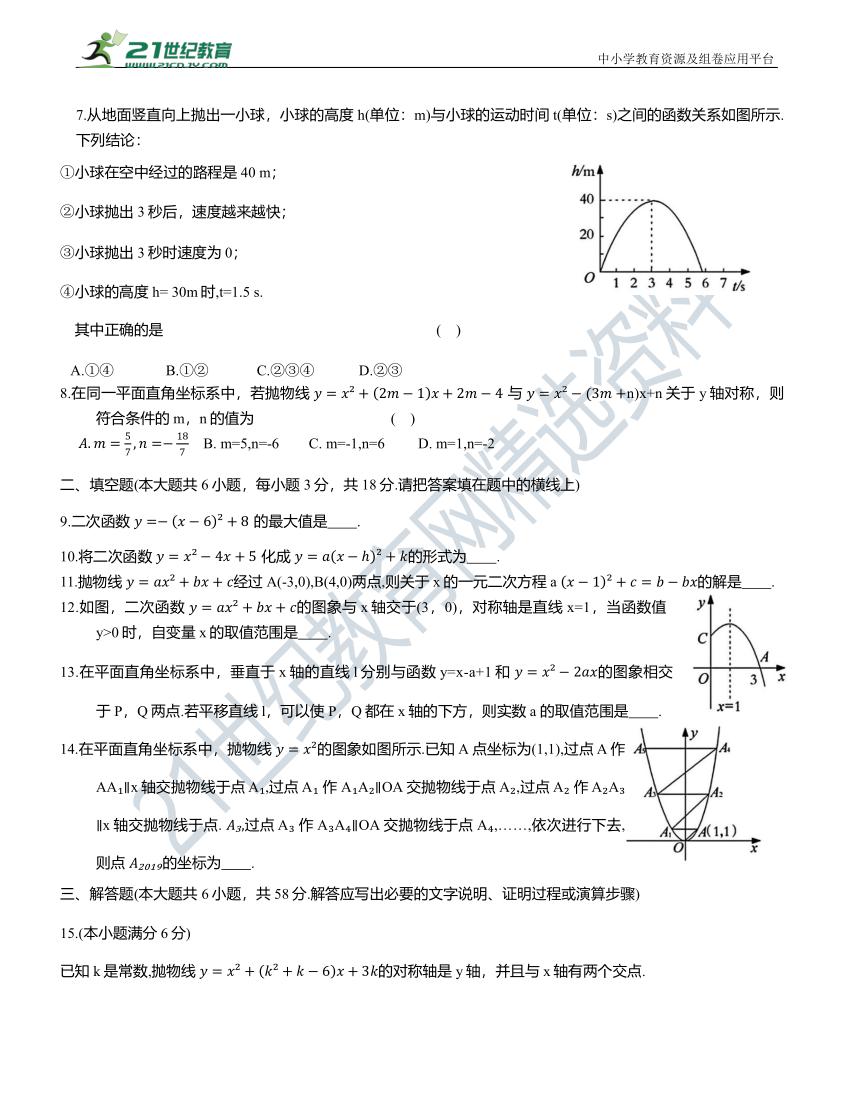
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是 40 m;
②小球抛出 3秒后,速度越来越快;
③小球抛出 3秒时速度为0;
④小球的高度 h= 30m时,t=1.5 s.
其中正确的是 ( )
A.①④ B.①② C.②③④ D.②③
8.在同一平面直角坐标系中,若抛物线 与 n)x+n关于y轴对称,则符合条件的 m,n的值为 ( )
B. m=5,n=-6 C. m=-1,n=6 D. m=1,n=-2
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.二次函数 的最大值是 .
10.将二次函数 化成 的形式为 .
11.抛物线 经过A(-3,0),B(4,0)两点,则关于x的一元二次方程a 的解是 .
12.如图,二次函数 的图象与x轴交于(3,0),对称轴是直线 x=1,当函数值 y>0时,自变量x的取值范围是 .
13.在平面直角坐标系中,垂直于x轴的直线l分别与函数y=x-a+1和 的图象相交于 P,Q两点.若平移直线 l,可以使 P,Q都在x轴的下方,则实数a 的取值范围是 .
14.在平面直角坐标系中,抛物线 的图象如图所示.已知A点坐标为(1,1),过点 A 作AA ∥x轴交抛物线于点 A ,过点 A 作A A ∥OA交抛物线于点A ,过点 A 作 A A ∥x轴交抛物线于点. 过点 A 作A A ∥OA交抛物线于点A ,……,依次进行下去,则点 的坐标为 .
三、解答题(本大题共 6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分6分)
中小学教育资源及组卷应用平台
已知 k是常数,抛物线 的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点 P在抛物线 上,且 P到 y轴的距离是2,求点 P 的坐标.
16.(本小题满分 10分)
如图,已知二次函数 的图象经过点
(1)求a的值和图象的顶点坐标;
(2)求 Q(m,n)在该二次函数的图象上.
①当m=2时,求n的值;
②若点 Q到 y轴的距离小于2,请根据图象直接写出n的取值范围.
17.(本小题满分 10分)
某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为 23米.
(1)设图中AB(与墙垂直的边)长为x米,则AD的长为 米(请用含x的代数式表示);
(2)若整个鸡场的总面积为 y米 ,求y的最大值.
18.(本小题满分10分)
如图1是某河上一座拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是 1m,拱桥的跨度为 10 m.桥洞与水面的最大距离是5 m.桥洞两侧壁上各有一盏距离水面4m 的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图2.
求:(1)抛物线的解析式;
(2)两盏景观灯 之间的水平距离.
19.(本小题满分 10分)
某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 60%.在销售过程中发现,这种儿童玩具每天的销售量 y(件)与销售单价x(元)满足一次函数关系.当销售单价为 35元时,每天的销售量为 350件;当销售单价为 40元时,每天的销售量为 300件.
(1)求y与x之间的函数关系式;
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少
20.(本小题满分 12分)
如图,已知抛物线 经过 两点,与 x轴的另一个交点为C,顶点为 D,连接 CD.
(1)求该抛物线的表达式;
(2)点 P为该抛物线上一动点(与点B,C不重合),设点 P 的横坐标为t.当点 P在直线 BC 的下方运动时,求 的面积的最大值;
一、1. A 2. A 3. B 4. D 5. D 6. D 7. D 8. D
二、9.8 10. y=(x-2) +1) 12.-11或a<-1
14.(-1010,1010 )
三、15.解:(1)抛物线 的对称轴是 y轴,∴x= 即 解得 k=-3或k=2.
当k=2时,二次函数解析式为 它的图象与 x轴无交点,不满足题意,舍去.
当k=-3时,二次函数解析式为 它的图象与 x轴有两个交点,满足题意.
∴k=-3.
(2)∵P到y轴的距离为2,∴点 P 的横坐标为—2或2.
当x=2时,y=-5;当x=-2时,y=-5.
∴点P的坐标为(2,-5)或(-2,-5).
16.解:(1)把 P(-2,3)代入 得 解得 a=2.
∴顶点坐标为(-1,2).
(2)①把x=2代入 求得 y=11,∴当m=2时,n=11.
②2≤n<11.
17.(1)(24—2x) (2)y的最大值是 72米
18.解:(1)由已知可得抛物线的顶点坐标为(5,5),与y轴的交点坐标是(0,1),可设抛物线的解析或是 把(0,1)代入 +5,解得
(2)由已知得两景观灯的纵坐标都是 4,代入(1)中的解析式得
解得 ··两景观灯间的距离为 (米).
19.(1)设y与x之间的函数关系式是y=kx+b,当x=35时,y=350;当x=40时,y=300,
(2)设利润为 w元.∵x≤30×(1+60%)=48,∴x≤48,w=(-10x+700)(x-30)=-10x +1000x-21000=-10(x-50) +4 000,
∵a=―10<0,抛物线开口向下,对称轴为x=50,当x<50时,w随x的增大而增大,又x≤48,∴当x=48时, 3 960.
答:销售单价为 48元时,该网店销售这种儿童玩具每天获得的利润最大,最大为 3 960元.
20.解:(1)∵抛物线 经过点 A(-5,0),B(-4,-3),
解得
∴该抛物线的表达式为
(2)如图,过点 P 作 PE⊥x轴于点 E,交直线 BC 于点F.
在抛物线 中,令y=0,则. 解得
∴点C的坐标为(―1,0).由点B(―4,―3)和C(―1,0),可得直线 BC的表达式为y=x+1.
设点 P 的坐标为 由题知-4当 时,△PBC的面积的最大值为
(时间:100 分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列是二次函数的是 ( )
B. y=2x+1
2.将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线解析式为( )
3.已知抛物线 经过(-2,n)和(4,n)两点,则n的值为 ( )
A.-2 B. -4 C.2 D.4
4.已知二次函数 关于该函数在-1≤x≤3的取值范围内,下列说法正确的是 ( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值―2
5.如图,二次函数 的图象经过点A(1,0),B(5,0),下列说法正确的是 ( )
A. c<0
C. a-b+c<0
D.图象的对称轴是直线x=3
6.若二次函数 的图象过不同的五点A(m,n),B(0,y ),C(3-m,n),D( ,y ),E(2,y ),!,则 y ,y ,y 的大小关系是 ( )
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是 40 m;
②小球抛出 3秒后,速度越来越快;
③小球抛出 3秒时速度为0;
④小球的高度 h= 30m时,t=1.5 s.
其中正确的是 ( )
A.①④ B.①② C.②③④ D.②③
8.在同一平面直角坐标系中,若抛物线 与 n)x+n关于y轴对称,则符合条件的 m,n的值为 ( )
B. m=5,n=-6 C. m=-1,n=6 D. m=1,n=-2
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.二次函数 的最大值是 .
10.将二次函数 化成 的形式为 .
11.抛物线 经过A(-3,0),B(4,0)两点,则关于x的一元二次方程a 的解是 .
12.如图,二次函数 的图象与x轴交于(3,0),对称轴是直线 x=1,当函数值 y>0时,自变量x的取值范围是 .
13.在平面直角坐标系中,垂直于x轴的直线l分别与函数y=x-a+1和 的图象相交于 P,Q两点.若平移直线 l,可以使 P,Q都在x轴的下方,则实数a 的取值范围是 .
14.在平面直角坐标系中,抛物线 的图象如图所示.已知A点坐标为(1,1),过点 A 作AA ∥x轴交抛物线于点 A ,过点 A 作A A ∥OA交抛物线于点A ,过点 A 作 A A ∥x轴交抛物线于点. 过点 A 作A A ∥OA交抛物线于点A ,……,依次进行下去,则点 的坐标为 .
三、解答题(本大题共 6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分6分)
中小学教育资源及组卷应用平台
已知 k是常数,抛物线 的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点 P在抛物线 上,且 P到 y轴的距离是2,求点 P 的坐标.
16.(本小题满分 10分)
如图,已知二次函数 的图象经过点
(1)求a的值和图象的顶点坐标;
(2)求 Q(m,n)在该二次函数的图象上.
①当m=2时,求n的值;
②若点 Q到 y轴的距离小于2,请根据图象直接写出n的取值范围.
17.(本小题满分 10分)
某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为 23米.
(1)设图中AB(与墙垂直的边)长为x米,则AD的长为 米(请用含x的代数式表示);
(2)若整个鸡场的总面积为 y米 ,求y的最大值.
18.(本小题满分10分)
如图1是某河上一座拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是 1m,拱桥的跨度为 10 m.桥洞与水面的最大距离是5 m.桥洞两侧壁上各有一盏距离水面4m 的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图2.
求:(1)抛物线的解析式;
(2)两盏景观灯 之间的水平距离.
19.(本小题满分 10分)
某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 60%.在销售过程中发现,这种儿童玩具每天的销售量 y(件)与销售单价x(元)满足一次函数关系.当销售单价为 35元时,每天的销售量为 350件;当销售单价为 40元时,每天的销售量为 300件.
(1)求y与x之间的函数关系式;
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少
20.(本小题满分 12分)
如图,已知抛物线 经过 两点,与 x轴的另一个交点为C,顶点为 D,连接 CD.
(1)求该抛物线的表达式;
(2)点 P为该抛物线上一动点(与点B,C不重合),设点 P 的横坐标为t.当点 P在直线 BC 的下方运动时,求 的面积的最大值;
一、1. A 2. A 3. B 4. D 5. D 6. D 7. D 8. D
二、9.8 10. y=(x-2) +1) 12.-1
14.(-1010,1010 )
三、15.解:(1)抛物线 的对称轴是 y轴,∴x= 即 解得 k=-3或k=2.
当k=2时,二次函数解析式为 它的图象与 x轴无交点,不满足题意,舍去.
当k=-3时,二次函数解析式为 它的图象与 x轴有两个交点,满足题意.
∴k=-3.
(2)∵P到y轴的距离为2,∴点 P 的横坐标为—2或2.
当x=2时,y=-5;当x=-2时,y=-5.
∴点P的坐标为(2,-5)或(-2,-5).
16.解:(1)把 P(-2,3)代入 得 解得 a=2.
∴顶点坐标为(-1,2).
(2)①把x=2代入 求得 y=11,∴当m=2时,n=11.
②2≤n<11.
17.(1)(24—2x) (2)y的最大值是 72米
18.解:(1)由已知可得抛物线的顶点坐标为(5,5),与y轴的交点坐标是(0,1),可设抛物线的解析或是 把(0,1)代入 +5,解得
(2)由已知得两景观灯的纵坐标都是 4,代入(1)中的解析式得
解得 ··两景观灯间的距离为 (米).
19.(1)设y与x之间的函数关系式是y=kx+b,当x=35时,y=350;当x=40时,y=300,
(2)设利润为 w元.∵x≤30×(1+60%)=48,∴x≤48,w=(-10x+700)(x-30)=-10x +1000x-21000=-10(x-50) +4 000,
∵a=―10<0,抛物线开口向下,对称轴为x=50,当x<50时,w随x的增大而增大,又x≤48,∴当x=48时, 3 960.
答:销售单价为 48元时,该网店销售这种儿童玩具每天获得的利润最大,最大为 3 960元.
20.解:(1)∵抛物线 经过点 A(-5,0),B(-4,-3),
解得
∴该抛物线的表达式为
(2)如图,过点 P 作 PE⊥x轴于点 E,交直线 BC 于点F.
在抛物线 中,令y=0,则. 解得
∴点C的坐标为(―1,0).由点B(―4,―3)和C(―1,0),可得直线 BC的表达式为y=x+1.
设点 P 的坐标为 由题知-4
同课章节目录
