圆锥曲线综合压轴之离心率问题 学案
文档属性
| 名称 | 圆锥曲线综合压轴之离心率问题 学案 |  | |
| 格式 | |||
| 文件大小 | 447.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 20:48:05 | ||
图片预览


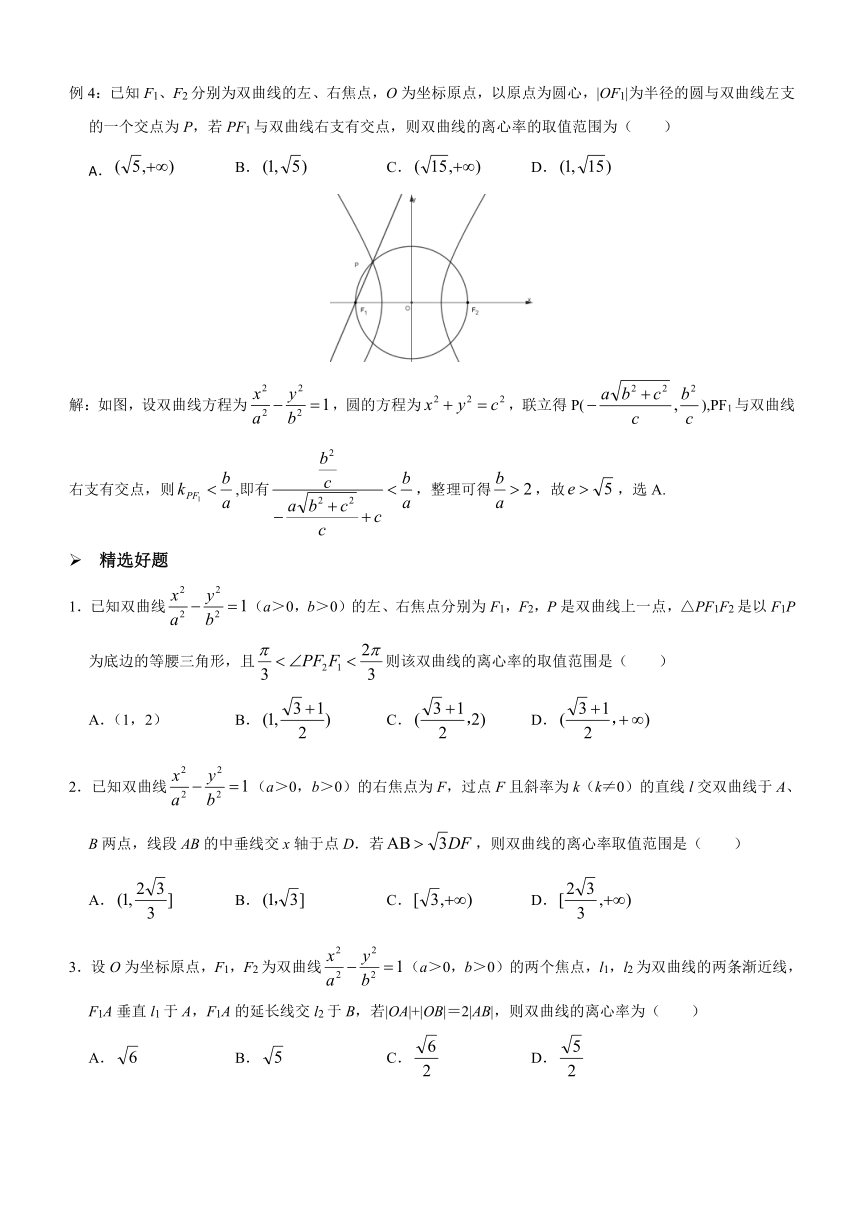

文档简介
离心率问题
e c c
2 b2
1. 1 1, (a2 b2 2椭圆离心率 c )
a a2 a2
c c2 b2
2. 双曲线离心率 e 2 1 2 1, (a
2 b2 c2 )
a a a
3. 常用二级结论:设圆锥曲线 C的焦点 F在 x 轴上,过点 F且斜率为 k的直线 l交曲线 C于 A、B两点,若
AF FB( 0) 2 1 1 ,则 e 1 k | |,设直线倾斜角为 ,则有 | ecos | | | .特别地,对于抛物线
1 1
有 | cos | 1 | |
1
经典举例
x2 y2
例 1:已知椭圆 C: 2 2 1(a b 0)的左右焦点分别为 F1,F2,点 A是椭圆上一点,线段 AF1的垂直平a b
分线与椭圆的一个交点为 B,若AB 3F2B,则椭圆 C的离心率为( )
1 3 2 6
A. B. C. D.
3 3 3 3
解:如上左图,AB 3F2B得 A、F2、B共线,AF2 F2B 3F2B得AF2 2F2B,设 BF2=m,则 AF2=2m,,
b
AB=3m,故BF1=3m,BF1+BF2=4m,得AF1=2m,AF1=AF2,故A为上顶点或下顶点.如上右图,作BD⊥x轴得BD= ,
2
c 3c , b c 3DF2= 即 B( ),代入椭圆方程得 ,选 B
2 2 2 a 3
点评:画出草图,利用向量关系、垂直平分线、椭圆的性质得到点 A处于特殊位置,利用相似得到点 B坐标,
进而得到离心率.
x2 y2
例 2:已知椭圆 2 2 1(a b 0)的左、右焦点分别为 F1,F2,P为椭圆上不与左、右顶点重合的任意一a b
点,I,G分别为△PF1F2的内心和重心,当 IG⊥x轴时,椭圆的离心率为( )
1 1 3 6
A. B. C. D.
3 2 2 3
x0 , y0 (PF1 PF解:设 P(x ,y ),重心 G( ),同时 2 F1F2 )r 1 2c y cy x cy0 0 0得 r 0 得 I( 0 , 0 ),在 PDI3 3 2 2 a c 3 a c
cy 1 2 2
中,PD2+DI2=PI2,即有 (a c)2 ( 0 )2 (x0 x )
2 cy x y
0 (y0 0 )
2
得 09
0
2 1又a c 3 a c (a c)2 b
4
x 2 20 y 02 2 1
2 9
得 a (a c)2 c 1得 ,故选 A
a b 4 a 3
点评:明显此题对同学们的基本功底有一定的要求,例如重心坐标公式、三角形内切圆半径的求解.
x2 y2 x2 y2
例 3:已知椭圆 C1: 2 2 1(a1 b1 0)与双曲线 C2: 2 2 1(a2 0,b2 0)有相同的焦点 F1,F2,a1 b1 a2 b2
点 P是两曲线在第一象限的交点,且F1F2在F1P上的投影等于|F1P |,e1,e2分别是椭圆 C1和双曲线 C2的离
心率,则 9e12+e22的最小值是( )
A.4 B.6 C.8 D.16
解:F1F2在F1P上的投影等于|F1P |,可知 PF1⊥PF2于是PF
2
1 PF
2 F 2 22 1F2 即有PF1 PF
2
2 4c
2
,同时
PF1 PF2 2a1,PF1 PF2 2a2两边同时平方得
PF 2 PF 2 2PF PF 4a 2 , PF 2 PF 2 2PF 1 11 2 1 2 1 1 2 1 PF2 4a
2
2 ,两式相加得 2 2 2,于是e1 e2
2 2 2 2 2 2
9e2 e2 11 2 (9e
2
1 e
2 )( 1 1 ) 1 (10 e2 9e1 12 2 2 2 2 ) (10 2
e2 9e 1 ) 8 e 9e2 2 ,当且仅当
2
2
1 即
2 e1 e2 2 e1 e2 2 e1 e2 e1 e
2
2
e2 3e1时成立,故选 C
例 4:已知 F1、F2分别为双曲线的左、右焦点,O为坐标原点,以原点为圆心,|OF1|为半径的圆与双曲线左支
的一个交点为 P,若 PF1与双曲线右支有交点,则双曲线的离心率的取值范围为( )
A. ( 5, ) B. (1, 5) C. ( 15, ) D. (1, 15)
x2 y2 2 2 2
1 x2 y2 c2 a b c b解:如图,设双曲线方程为 2 2 ,圆的方程为 ,联立得 P( , ),PF1与双曲线a b c c
b2
b b b
右支有交点,则 kPF ,即有 c ,整理可得 2,故 e 5 ,选 A.1 a a b2 c2 a a
c
c
精选好题
x2 y2
1.已知双曲线 2 2 1(a>0,b>0)的左、右焦点分别为 F1,F2,P是双曲线上一点,△PF1F2是以 F1Pa b
PF F 2 为底边的等腰三角形,且 2 1 则该双曲线的离心率的取值范围是( )3 3
3 1 3 1 3 1
A.(1,2) B. (1, ) C. ( ,2) D. ( , )
2 2 2
x2 y2
2.已知双曲线 2 2 1(a>0,b>0)的右焦点为 F,过点 F且斜率为 k(k≠0)的直线 l交双曲线于 A、a b
B两点,线段 AB的中垂线交 x轴于点 D.若AB 3DF,则双曲线的离心率取值范围是( )
A. (1, 2 3 ] B. (1,3] [ 3, 2 3C. ) D.[ , )
3 3
x2 y2
3.设 O为坐标原点,F1,F2为双曲线 2 2 1(a>0,b>0)的两个焦点,l1,l2为双曲线的两条渐近线,a b
F1A垂直 l1于 A,F1A的延长线交 l2于 B,若|OA|+|OB|=2|AB|,则双曲线的离心率为( )
6 5
A. 6 B. 5 C. D.
2 2
4.已知 F1,F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且 F1P>F2P,线段 F1P的垂直平分线过
2 e
F2.若椭圆的离心率为 e1,双曲线的离心率为 e ,则 22 的最小值为( )
e1 2
A. 6 B.3 C.6 D. 3
x2 y2
5.已知双曲线 C: 2 2 1(a>0,b>0)的右焦点为 F,若以 OF(O为坐标原点)为直径的圆被双曲线a b
C的一条渐近线所截得的弦长等于双曲线 C的虚轴长,则双曲线 C的离心率为( )
5 5
A. B. 2 C. D.2
2 4
x2 y2
6.已知 F1、F2分别是双曲线 C: 2 2 1(a>0,b>0)的左、右焦点,过点 F1向一条渐近线作垂线,a b
交双曲线右支于点 P,直线 F2P与 y轴交于点 Q(P,Q在轴同侧),连接 QF1,若△PQF1的内切圆圆心恰
好落在以 F1F2为直径的圆上,则双曲线的离心率为( )
A. 3 B. 2 C. 5 D.2
x2 y2
7.已知双曲线 C: 2 2 1(a>0,b>0)的左、右焦点分别为 F1(﹣c,0),F2(c,0),过点 F1的直a b
8
线 l(斜率存在)交双曲线 C 的渐近线于 A,B 两点,若 |F2A|= |F2B|, S AF F S c
2
=
1 2 BF1F2 5
(S AF 、S 表示△AF1F2,△BF1F2的面积),则双曲线 C的离心率为( )1F2 BF1F2
6
A. 3 B. C. 5 15D.
2 3
x2 y2
8.已知双曲线 C: 2 2 1(a>0,b>0),若双曲线不存在以点(2a,a)为中点的弦,则双曲线离心率a b
e的取值范围是( )
2 3 5 2 3
A.(1, ] B.[ , ] 2 3C.[ , ) D.[ 5, ]
3 2 3 3 2
x2 y2
9.设椭圆 C: 2 2 1(a b 0)的右焦点为 F,椭圆 C上的两点 A、B关于原点对称,且满足FA FB 0,a b
|FB|≤|FA|≤2|FB|,则椭圆 C的离心率的取值范围是( )
2 5 5
A.[ , ] B.[ ,1) [ 2C. , 3 1] D.[ 3 1,1)
2 3 3 2
x2 y2
10.已知直线 y=kx(k≠0)与双曲线 2 2 1(a>0,b>0)交于 A,B两点,以 AB为直径的圆恰好经a b
过双曲线的右焦点 F,若△ABF的面积为 4a2,则双曲线的离心率为( )
A. 2 B. 3 C.2 D. 5
11.如图,α,β,γ是由直线 l引出的三个不重合的半平面,其中二面角α﹣l﹣β大小为 60°,γ在二面角α﹣l
﹣β内绕直线 l旋转,圆 C在γ内,且圆 C在α,β内的射影分别为椭圆 C1,C2.记椭圆 C1,C2的离心率分
别为 e1,e2,则 e12+e22的取值范围是( )
1 3 1 5 1 3 1 5
A.[ , ) B.[ , ) C.[ , ) D.[ , )
3 4 3 4 2 4 2 4
x2 y2
12.已知椭圆 2 2 1(a b 0)的左、右焦点分别为 F1,F2,P为椭圆上不与左、右顶点重合的任意一点,a b
I,G分别为△PF1F2的内心和重心,当 IG⊥x轴时,椭圆的离心率为( )
1 1 3 6
A. B. C. D.
3 2 2 3
13.椭圆的焦点F1( 2 2,0),F2 (2 2,0)长轴长为 2a,在椭圆上存在点 P,使∠F1PF2=90°,对于直线 y=
a,在圆 x2+(y﹣1)2=2 上始终存在两点 M,N使得直线上有点 Q,满足∠MQN=90°,则椭圆的离心率
的取值范围是( )
2 2
A.[ ,1) [ 2 ,1) [ 2 , 2 2 ] 2 2B. C. D. (0, ]
3 2 2 3 3
x2 y2
14.过双曲线 C: 2 2 1(a>0,b>0)右焦点 F的直线 l与 C交于 P,Q两点,,若QP 2PF,QP FQ 0,a b
则 C的离心率为( )
A. 2 B.2 C. 7 D. 10
x2 y2 1
15.已知双曲线 E: 2 2 1(a>0,b>0),斜率为 的直线与 E的左右两支分别交于 A,B两点,点 Pa b 8
1
的坐标为(﹣1,2),直线 AP交 E于另一点 C,直线 BP交 E于另一点 D.若直线 CD的斜率为 ,则 E
8
的离心率为( )
6 3 5 5
A. B. C. D.
2 2 2 2
x2 y2
16.设椭圆 C: 2 2 1(a b 0)的左,右顶点为 A,B.P是椭圆上不同于 A,B的一点,设直线 AP,a b
a
BP的斜率分别为 m,n,则当 +ln|m|+ln|n|取得最小值时,椭圆 C的离心率为( )
b
1 2 4 3
A. B. C. D.
5 2 5 2
x2 y2
17.设椭圆 C: 2 2 1(a b 0)的左,右顶点为 A,B.P是椭圆上不同于 A,B的一点,设直线 AP,a b
a 2 2
BP的斜率分别为 m,n,则当 (3﹣ )+ +3(ln|m|+ln|n|)取得最小值时,椭圆 C的离心率为( )
b 3mn mn
1 2 4 3
A. B. C. D.
5 2 5 2
x2 y2
18.设 F1,F2为双曲线 2 2 1(a>0,b>0)的左、右焦点,点 P(x0,2a)为双曲线上的一点,若△a b
PF1F2的重心和内心的连线与 x轴垂直,则双曲线的离心率为( )
6 5
A. B. C. 6 D. 5
2 2
x2 y2
19.过双曲线 C: 2 2 1(a>0,b>0)左焦点 F的直线 l与 C交于 M,N两点,且FN 3FM,若 OMa b
⊥FN,则 C的离心率为( )
A.2 B. 7 C.3 D. 10
x2 y2
20.已知椭圆 C: 2 1(a b 0)的左右焦点分别为 F1,F2,点 A是椭圆上一点,线段 AF1的垂直平a b2
分线与椭圆的一个交点为 B,若AB 3F2B则椭圆 C的离心率为( )
1 3 2 6
A. B. C. D.
3 3 3 3
x2 y2
21.已知 O为坐标原点,A,B分别是椭圆 C: 2 2 1(a b 0)的左,右顶点,抛物线 E:y
2=2px(p
a b
OP'
>0)与椭圆 C在第一象限交于点 P,点 P在 x轴上的投影为 P’,且有OP =c(其中 c2=a2﹣b2),
| OP'|
AP的连线与 y轴交于点 M,BM与 PP'的交点 N恰为 PP'的中点,则椭圆 C的离心率为( )
3 2 2 1
A. B. C. D.
2 2 3 3
x2 y2
22.已知点 P(x0,y0)(x0≠±a)在椭圆 C: 2 2 1(a b 0)上,若点 M为椭圆 C的右顶点,且 POa b
⊥PM(O为坐标原点),则椭圆 C的离心率 e的取值范围是( )
3 3 2 2
A.(0, ) B.( ,1) C.( ,1) D.(0, )
3 3 2 2
23.已知椭圆与双曲线有公共焦点,F1,F2,F1为左焦点,F2为右焦点,P点为它们在第一象限的一个交点,
1 1
且∠F1PF2= ,设 e1,e2分别为椭圆双曲线离心率,则 的最大值为( )
4 e1 e2
A. 2 B.2 2 C.3 2 D.4 2
x2 y2
24.已知 F1,F2是椭圆 E: 2 2 1(a b 0)的左、右焦点,若 E上存在不同两点 A,B,使得 Fa b 1
A 3 F2B
则该椭圆的离心率的取值范围为( )
A.( 3﹣1,1) B.(0, 3﹣1) C.(2﹣ 3,1) D.(0,2﹣ 3)
x2
25.点 A 2是椭圆 2 y 1(a>1)的上顶点,B、C是该椭圆的另外两点,且△ABC是以点 A为直角顶点的a
等腰直角三角形,若满足条件的△ABC只有一个,则椭圆的离心率 e的范围是( )
3 3 6 6
A. ≤e<1 B.0<e≤ C.0<e≤ D. ≤e<1
3 3 3 3
x2 y2
26.已知 F1,F2是椭圆 C: 2 2 1(a b 0)的焦点,P是椭圆 C上一点,若 I是△PF1F2的内心,且满a b
足 2 IF1 3IF2 4 IP 0则 C的离心率 e的值是( )
2 2 1 4
A. B. C. D.
9 7 2 5
参考答案
1. D 2.A 3.B 4.C 5.A 6.C 7.D 8.B 9.A 10.D 11.C 12.A 13.A
14.C 15.C 16.D 17.A 18.A 19.B 20.B 21.D 22.C 23.B 24.C
25.C 26.D
e c c
2 b2
1. 1 1, (a2 b2 2椭圆离心率 c )
a a2 a2
c c2 b2
2. 双曲线离心率 e 2 1 2 1, (a
2 b2 c2 )
a a a
3. 常用二级结论:设圆锥曲线 C的焦点 F在 x 轴上,过点 F且斜率为 k的直线 l交曲线 C于 A、B两点,若
AF FB( 0) 2 1 1 ,则 e 1 k | |,设直线倾斜角为 ,则有 | ecos | | | .特别地,对于抛物线
1 1
有 | cos | 1 | |
1
经典举例
x2 y2
例 1:已知椭圆 C: 2 2 1(a b 0)的左右焦点分别为 F1,F2,点 A是椭圆上一点,线段 AF1的垂直平a b
分线与椭圆的一个交点为 B,若AB 3F2B,则椭圆 C的离心率为( )
1 3 2 6
A. B. C. D.
3 3 3 3
解:如上左图,AB 3F2B得 A、F2、B共线,AF2 F2B 3F2B得AF2 2F2B,设 BF2=m,则 AF2=2m,,
b
AB=3m,故BF1=3m,BF1+BF2=4m,得AF1=2m,AF1=AF2,故A为上顶点或下顶点.如上右图,作BD⊥x轴得BD= ,
2
c 3c , b c 3DF2= 即 B( ),代入椭圆方程得 ,选 B
2 2 2 a 3
点评:画出草图,利用向量关系、垂直平分线、椭圆的性质得到点 A处于特殊位置,利用相似得到点 B坐标,
进而得到离心率.
x2 y2
例 2:已知椭圆 2 2 1(a b 0)的左、右焦点分别为 F1,F2,P为椭圆上不与左、右顶点重合的任意一a b
点,I,G分别为△PF1F2的内心和重心,当 IG⊥x轴时,椭圆的离心率为( )
1 1 3 6
A. B. C. D.
3 2 2 3
x0 , y0 (PF1 PF解:设 P(x ,y ),重心 G( ),同时 2 F1F2 )r 1 2c y cy x cy0 0 0得 r 0 得 I( 0 , 0 ),在 PDI3 3 2 2 a c 3 a c
cy 1 2 2
中,PD2+DI2=PI2,即有 (a c)2 ( 0 )2 (x0 x )
2 cy x y
0 (y0 0 )
2
得 09
0
2 1又a c 3 a c (a c)2 b
4
x 2 20 y 02 2 1
2 9
得 a (a c)2 c 1得 ,故选 A
a b 4 a 3
点评:明显此题对同学们的基本功底有一定的要求,例如重心坐标公式、三角形内切圆半径的求解.
x2 y2 x2 y2
例 3:已知椭圆 C1: 2 2 1(a1 b1 0)与双曲线 C2: 2 2 1(a2 0,b2 0)有相同的焦点 F1,F2,a1 b1 a2 b2
点 P是两曲线在第一象限的交点,且F1F2在F1P上的投影等于|F1P |,e1,e2分别是椭圆 C1和双曲线 C2的离
心率,则 9e12+e22的最小值是( )
A.4 B.6 C.8 D.16
解:F1F2在F1P上的投影等于|F1P |,可知 PF1⊥PF2于是PF
2
1 PF
2 F 2 22 1F2 即有PF1 PF
2
2 4c
2
,同时
PF1 PF2 2a1,PF1 PF2 2a2两边同时平方得
PF 2 PF 2 2PF PF 4a 2 , PF 2 PF 2 2PF 1 11 2 1 2 1 1 2 1 PF2 4a
2
2 ,两式相加得 2 2 2,于是e1 e2
2 2 2 2 2 2
9e2 e2 11 2 (9e
2
1 e
2 )( 1 1 ) 1 (10 e2 9e1 12 2 2 2 2 ) (10 2
e2 9e 1 ) 8 e 9e2 2 ,当且仅当
2
2
1 即
2 e1 e2 2 e1 e2 2 e1 e2 e1 e
2
2
e2 3e1时成立,故选 C
例 4:已知 F1、F2分别为双曲线的左、右焦点,O为坐标原点,以原点为圆心,|OF1|为半径的圆与双曲线左支
的一个交点为 P,若 PF1与双曲线右支有交点,则双曲线的离心率的取值范围为( )
A. ( 5, ) B. (1, 5) C. ( 15, ) D. (1, 15)
x2 y2 2 2 2
1 x2 y2 c2 a b c b解:如图,设双曲线方程为 2 2 ,圆的方程为 ,联立得 P( , ),PF1与双曲线a b c c
b2
b b b
右支有交点,则 kPF ,即有 c ,整理可得 2,故 e 5 ,选 A.1 a a b2 c2 a a
c
c
精选好题
x2 y2
1.已知双曲线 2 2 1(a>0,b>0)的左、右焦点分别为 F1,F2,P是双曲线上一点,△PF1F2是以 F1Pa b
PF F 2 为底边的等腰三角形,且 2 1 则该双曲线的离心率的取值范围是( )3 3
3 1 3 1 3 1
A.(1,2) B. (1, ) C. ( ,2) D. ( , )
2 2 2
x2 y2
2.已知双曲线 2 2 1(a>0,b>0)的右焦点为 F,过点 F且斜率为 k(k≠0)的直线 l交双曲线于 A、a b
B两点,线段 AB的中垂线交 x轴于点 D.若AB 3DF,则双曲线的离心率取值范围是( )
A. (1, 2 3 ] B. (1,3] [ 3, 2 3C. ) D.[ , )
3 3
x2 y2
3.设 O为坐标原点,F1,F2为双曲线 2 2 1(a>0,b>0)的两个焦点,l1,l2为双曲线的两条渐近线,a b
F1A垂直 l1于 A,F1A的延长线交 l2于 B,若|OA|+|OB|=2|AB|,则双曲线的离心率为( )
6 5
A. 6 B. 5 C. D.
2 2
4.已知 F1,F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且 F1P>F2P,线段 F1P的垂直平分线过
2 e
F2.若椭圆的离心率为 e1,双曲线的离心率为 e ,则 22 的最小值为( )
e1 2
A. 6 B.3 C.6 D. 3
x2 y2
5.已知双曲线 C: 2 2 1(a>0,b>0)的右焦点为 F,若以 OF(O为坐标原点)为直径的圆被双曲线a b
C的一条渐近线所截得的弦长等于双曲线 C的虚轴长,则双曲线 C的离心率为( )
5 5
A. B. 2 C. D.2
2 4
x2 y2
6.已知 F1、F2分别是双曲线 C: 2 2 1(a>0,b>0)的左、右焦点,过点 F1向一条渐近线作垂线,a b
交双曲线右支于点 P,直线 F2P与 y轴交于点 Q(P,Q在轴同侧),连接 QF1,若△PQF1的内切圆圆心恰
好落在以 F1F2为直径的圆上,则双曲线的离心率为( )
A. 3 B. 2 C. 5 D.2
x2 y2
7.已知双曲线 C: 2 2 1(a>0,b>0)的左、右焦点分别为 F1(﹣c,0),F2(c,0),过点 F1的直a b
8
线 l(斜率存在)交双曲线 C 的渐近线于 A,B 两点,若 |F2A|= |F2B|, S AF F S c
2
=
1 2 BF1F2 5
(S AF 、S 表示△AF1F2,△BF1F2的面积),则双曲线 C的离心率为( )1F2 BF1F2
6
A. 3 B. C. 5 15D.
2 3
x2 y2
8.已知双曲线 C: 2 2 1(a>0,b>0),若双曲线不存在以点(2a,a)为中点的弦,则双曲线离心率a b
e的取值范围是( )
2 3 5 2 3
A.(1, ] B.[ , ] 2 3C.[ , ) D.[ 5, ]
3 2 3 3 2
x2 y2
9.设椭圆 C: 2 2 1(a b 0)的右焦点为 F,椭圆 C上的两点 A、B关于原点对称,且满足FA FB 0,a b
|FB|≤|FA|≤2|FB|,则椭圆 C的离心率的取值范围是( )
2 5 5
A.[ , ] B.[ ,1) [ 2C. , 3 1] D.[ 3 1,1)
2 3 3 2
x2 y2
10.已知直线 y=kx(k≠0)与双曲线 2 2 1(a>0,b>0)交于 A,B两点,以 AB为直径的圆恰好经a b
过双曲线的右焦点 F,若△ABF的面积为 4a2,则双曲线的离心率为( )
A. 2 B. 3 C.2 D. 5
11.如图,α,β,γ是由直线 l引出的三个不重合的半平面,其中二面角α﹣l﹣β大小为 60°,γ在二面角α﹣l
﹣β内绕直线 l旋转,圆 C在γ内,且圆 C在α,β内的射影分别为椭圆 C1,C2.记椭圆 C1,C2的离心率分
别为 e1,e2,则 e12+e22的取值范围是( )
1 3 1 5 1 3 1 5
A.[ , ) B.[ , ) C.[ , ) D.[ , )
3 4 3 4 2 4 2 4
x2 y2
12.已知椭圆 2 2 1(a b 0)的左、右焦点分别为 F1,F2,P为椭圆上不与左、右顶点重合的任意一点,a b
I,G分别为△PF1F2的内心和重心,当 IG⊥x轴时,椭圆的离心率为( )
1 1 3 6
A. B. C. D.
3 2 2 3
13.椭圆的焦点F1( 2 2,0),F2 (2 2,0)长轴长为 2a,在椭圆上存在点 P,使∠F1PF2=90°,对于直线 y=
a,在圆 x2+(y﹣1)2=2 上始终存在两点 M,N使得直线上有点 Q,满足∠MQN=90°,则椭圆的离心率
的取值范围是( )
2 2
A.[ ,1) [ 2 ,1) [ 2 , 2 2 ] 2 2B. C. D. (0, ]
3 2 2 3 3
x2 y2
14.过双曲线 C: 2 2 1(a>0,b>0)右焦点 F的直线 l与 C交于 P,Q两点,,若QP 2PF,QP FQ 0,a b
则 C的离心率为( )
A. 2 B.2 C. 7 D. 10
x2 y2 1
15.已知双曲线 E: 2 2 1(a>0,b>0),斜率为 的直线与 E的左右两支分别交于 A,B两点,点 Pa b 8
1
的坐标为(﹣1,2),直线 AP交 E于另一点 C,直线 BP交 E于另一点 D.若直线 CD的斜率为 ,则 E
8
的离心率为( )
6 3 5 5
A. B. C. D.
2 2 2 2
x2 y2
16.设椭圆 C: 2 2 1(a b 0)的左,右顶点为 A,B.P是椭圆上不同于 A,B的一点,设直线 AP,a b
a
BP的斜率分别为 m,n,则当 +ln|m|+ln|n|取得最小值时,椭圆 C的离心率为( )
b
1 2 4 3
A. B. C. D.
5 2 5 2
x2 y2
17.设椭圆 C: 2 2 1(a b 0)的左,右顶点为 A,B.P是椭圆上不同于 A,B的一点,设直线 AP,a b
a 2 2
BP的斜率分别为 m,n,则当 (3﹣ )+ +3(ln|m|+ln|n|)取得最小值时,椭圆 C的离心率为( )
b 3mn mn
1 2 4 3
A. B. C. D.
5 2 5 2
x2 y2
18.设 F1,F2为双曲线 2 2 1(a>0,b>0)的左、右焦点,点 P(x0,2a)为双曲线上的一点,若△a b
PF1F2的重心和内心的连线与 x轴垂直,则双曲线的离心率为( )
6 5
A. B. C. 6 D. 5
2 2
x2 y2
19.过双曲线 C: 2 2 1(a>0,b>0)左焦点 F的直线 l与 C交于 M,N两点,且FN 3FM,若 OMa b
⊥FN,则 C的离心率为( )
A.2 B. 7 C.3 D. 10
x2 y2
20.已知椭圆 C: 2 1(a b 0)的左右焦点分别为 F1,F2,点 A是椭圆上一点,线段 AF1的垂直平a b2
分线与椭圆的一个交点为 B,若AB 3F2B则椭圆 C的离心率为( )
1 3 2 6
A. B. C. D.
3 3 3 3
x2 y2
21.已知 O为坐标原点,A,B分别是椭圆 C: 2 2 1(a b 0)的左,右顶点,抛物线 E:y
2=2px(p
a b
OP'
>0)与椭圆 C在第一象限交于点 P,点 P在 x轴上的投影为 P’,且有OP =c(其中 c2=a2﹣b2),
| OP'|
AP的连线与 y轴交于点 M,BM与 PP'的交点 N恰为 PP'的中点,则椭圆 C的离心率为( )
3 2 2 1
A. B. C. D.
2 2 3 3
x2 y2
22.已知点 P(x0,y0)(x0≠±a)在椭圆 C: 2 2 1(a b 0)上,若点 M为椭圆 C的右顶点,且 POa b
⊥PM(O为坐标原点),则椭圆 C的离心率 e的取值范围是( )
3 3 2 2
A.(0, ) B.( ,1) C.( ,1) D.(0, )
3 3 2 2
23.已知椭圆与双曲线有公共焦点,F1,F2,F1为左焦点,F2为右焦点,P点为它们在第一象限的一个交点,
1 1
且∠F1PF2= ,设 e1,e2分别为椭圆双曲线离心率,则 的最大值为( )
4 e1 e2
A. 2 B.2 2 C.3 2 D.4 2
x2 y2
24.已知 F1,F2是椭圆 E: 2 2 1(a b 0)的左、右焦点,若 E上存在不同两点 A,B,使得 Fa b 1
A 3 F2B
则该椭圆的离心率的取值范围为( )
A.( 3﹣1,1) B.(0, 3﹣1) C.(2﹣ 3,1) D.(0,2﹣ 3)
x2
25.点 A 2是椭圆 2 y 1(a>1)的上顶点,B、C是该椭圆的另外两点,且△ABC是以点 A为直角顶点的a
等腰直角三角形,若满足条件的△ABC只有一个,则椭圆的离心率 e的范围是( )
3 3 6 6
A. ≤e<1 B.0<e≤ C.0<e≤ D. ≤e<1
3 3 3 3
x2 y2
26.已知 F1,F2是椭圆 C: 2 2 1(a b 0)的焦点,P是椭圆 C上一点,若 I是△PF1F2的内心,且满a b
足 2 IF1 3IF2 4 IP 0则 C的离心率 e的值是( )
2 2 1 4
A. B. C. D.
9 7 2 5
参考答案
1. D 2.A 3.B 4.C 5.A 6.C 7.D 8.B 9.A 10.D 11.C 12.A 13.A
14.C 15.C 16.D 17.A 18.A 19.B 20.B 21.D 22.C 23.B 24.C
25.C 26.D
