人教版九年级数学上册第二十三章 旋转基础复习卷(一)(23.1)
文档属性
| 名称 | 人教版九年级数学上册第二十三章 旋转基础复习卷(一)(23.1) | 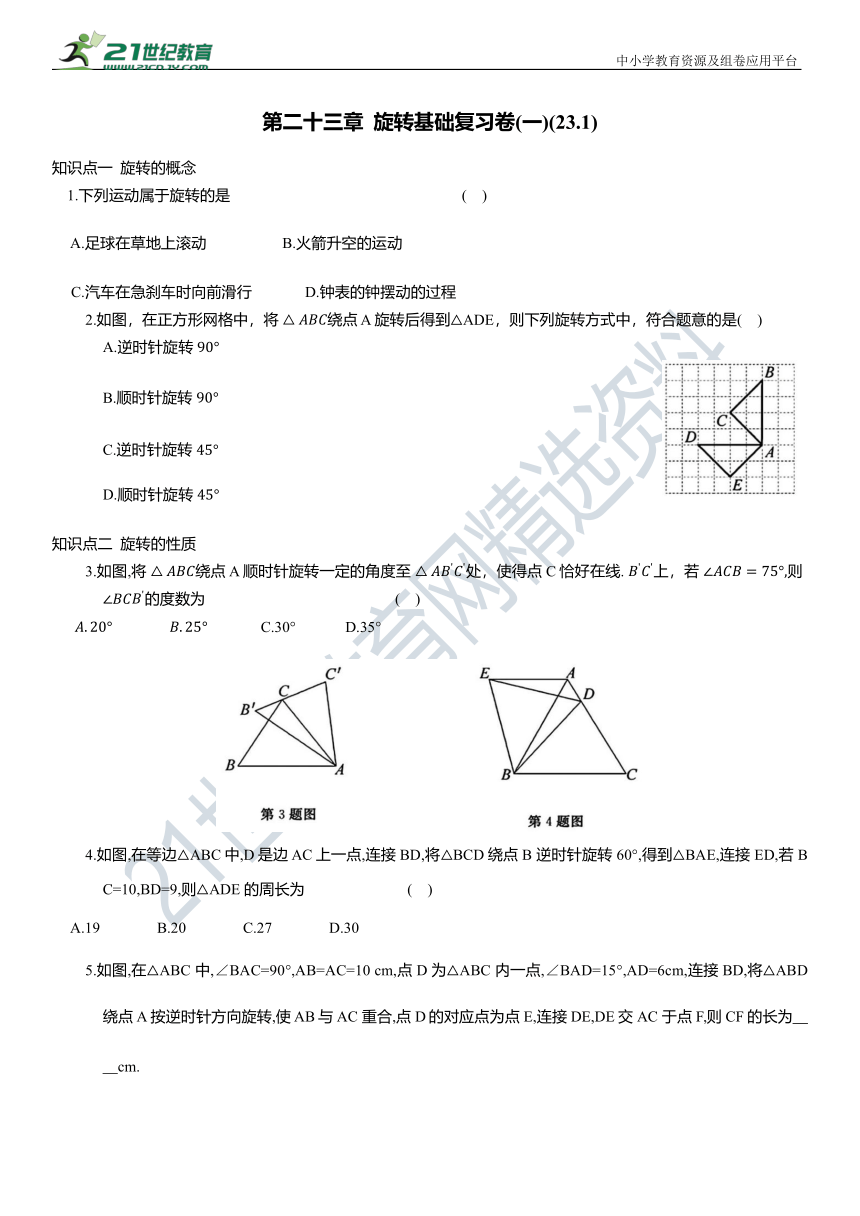 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 19:24:24 | ||
图片预览



文档简介
第二十三章 旋转基础复习卷(一)(23.1)
知识点一 旋转的概念
1.下列运动属于旋转的是 ( )
A.足球在草地上滚动 B.火箭升空的运动
C.汽车在急刹车时向前滑行 D.钟表的钟摆动的过程
2.如图,在正方形网格中,将 绕点 A 旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转
B.顺时针旋转
C.逆时针旋转
D.顺时针旋转
知识点二 旋转的性质
3.如图,将 绕点 A 顺时针旋转一定的角度至 处,使得点C恰好在线. 上,若 则 的度数为 ( )
C.30° D.35°
4.如图,在等边△ABC中,D是边 AC上一点,连接 BD,将△BCD绕点 B 逆时针旋转 60°,得到△BAE,连接 ED,若 BC=10,BD=9,则△ADE 的周长为 ( )
A.19 B.20 C.27 D.30
5.如图,在△ABC 中,∠BAC=90°,AB=AC=10 cm,点 D 为△ABC 内一点,∠BAD=15°,AD=6cm,连接 BD,将△ABD绕点A 按逆时针方向旋转,使 AB与AC 重合,点D的对应点为点E,连接DE,DE交AC 于点F,则CF的长为 cm.
6.一副三角板如图放置,将三角板 ADE 绕点A 逆时针旋转( ,使得三角板 ADE 的一边所在的直线与 BC 垂直,则α的度数为 .
知识点三 旋转作图
7.在如图 4×4 的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M N P ,则其旋转中心可能是 ( )
A.点 A B.点 B
C.点C D.点 D
8.如图,在正方形网格中有 绕O点按逆时针旋转 后的图案应该是 ( )
9.如图,在平面直角坐标系 xOy中,△ABC 的三个顶点坐标分别为
(1)将 绕点O逆时针旋转S 0°得到. ,请画出,
(2)点 的坐标为 .
中小学教育资源及组卷应用平台
(3)求 的面积.
知识点四 旋转证明题
10.已知 是等边三角形,D是BC上一点, 绕点A 逆时针旋转到 的位置.
(1)如图,旋转中心是 ,
(2)如图,如果M是AB 的中点,那么经过上述旋转后,点M转动了 ;
(3)如果点 D为 BC 边的三等分点,且. 的面积为 3,求四边形 ADCE 的面积.
11.如图,四边形 ABCD是正方形, 是等边三角形,M为对角线BD(不含 B、D点)上任意一点,将线段 BM绕点 B 逆时针旋转( °得到 BN,连接 EN、AM、CM.求证:
12.如图,△ABC中,点 E在BC 边上,AE=AB.将线段 AC绕点 A 旋转到 AF 的位置,使得∠CAF=∠BAE.连接 EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC 的度数.
13.在正方形 ABCD中,E是CD上的一点,
(1)如图1,将△ADE 绕点 A 顺时针方向旋转 90°,使 AD与AB 重合,得到△ABF,由旋转可知:DE= ,
∠AFB=∠
(2)如图2,正方形 ABCD中,P、Q分别是BC、CD边上一点,且∠PAQ=45°,试通过旋转的方法证明:DQ+BP=PQ;
(3)在(2)题中,连接 BD分别交AP、AQ于M、N,求证:
基础复习卷(一)23.1
1. D 2. A 3. C 4. A 5.10—2 6.60°或15° 7. B 8. A
9.(1)略 (2)(1,―4) (3)3.5 10.(1)点 A 60° (2)60° (3)9
11.证明:由旋转性质可知:BN=BM,∵△BAE为等边三角形,∴∠EBA=60°,BA=BE,
又 ∵ ∠MBN = 60°, ∴ ∠NBE = ∠MBA, 在 △ABM 和 △EBN
中
∴△ABM≌△EBN,∴AM=EN.
12.解:(1)证明:∵线段 AC绕点A 旋转到AF 的位置,∴AC=AF.
∵∠CAF=∠BAE, ∴ ∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.
在△ABC和△AEF中
∴△ABC≌△AEF(SAS),∴EF=BC.
(2)∵AF=AB,∴∠AEB=∠ABC=65°.
∴△ABC≌△AEF,∴∠AEF=∠ABC=65°,∠FEC=180°-∠AEB-∠AEF=180°-65°-65°=50°,
∵∠FGC是△EGC的外角,∠ACB=28°,∴∠FGC=∠FEC+∠ACB=50°+28°=78°.
13.(1)BF,AED;
(2)将△ADQ绕点A 按顺时针方向旋转90°,则AD与AB 重合,得到△ABE,如图,则∠D=∠ABE=90°,即点 E,B,P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,∴∠PAE=45°,∴∠PAQ=∠PAE,
在△APE和△APQ中,
PE=PQ,
而 PE=PB+BE=PB+DQ,∴DQ+BP=PQ;
(3)∵四边形 ABCD为正方形,∴∠ABD=∠ADB=45°,如图,将△ADN绕点 A 按顺时针方向旋转 90°,则 AD与 AB重合,得到△ABK,则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到 MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK 为直角三角形,
知识点一 旋转的概念
1.下列运动属于旋转的是 ( )
A.足球在草地上滚动 B.火箭升空的运动
C.汽车在急刹车时向前滑行 D.钟表的钟摆动的过程
2.如图,在正方形网格中,将 绕点 A 旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转
B.顺时针旋转
C.逆时针旋转
D.顺时针旋转
知识点二 旋转的性质
3.如图,将 绕点 A 顺时针旋转一定的角度至 处,使得点C恰好在线. 上,若 则 的度数为 ( )
C.30° D.35°
4.如图,在等边△ABC中,D是边 AC上一点,连接 BD,将△BCD绕点 B 逆时针旋转 60°,得到△BAE,连接 ED,若 BC=10,BD=9,则△ADE 的周长为 ( )
A.19 B.20 C.27 D.30
5.如图,在△ABC 中,∠BAC=90°,AB=AC=10 cm,点 D 为△ABC 内一点,∠BAD=15°,AD=6cm,连接 BD,将△ABD绕点A 按逆时针方向旋转,使 AB与AC 重合,点D的对应点为点E,连接DE,DE交AC 于点F,则CF的长为 cm.
6.一副三角板如图放置,将三角板 ADE 绕点A 逆时针旋转( ,使得三角板 ADE 的一边所在的直线与 BC 垂直,则α的度数为 .
知识点三 旋转作图
7.在如图 4×4 的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M N P ,则其旋转中心可能是 ( )
A.点 A B.点 B
C.点C D.点 D
8.如图,在正方形网格中有 绕O点按逆时针旋转 后的图案应该是 ( )
9.如图,在平面直角坐标系 xOy中,△ABC 的三个顶点坐标分别为
(1)将 绕点O逆时针旋转S 0°得到. ,请画出,
(2)点 的坐标为 .
中小学教育资源及组卷应用平台
(3)求 的面积.
知识点四 旋转证明题
10.已知 是等边三角形,D是BC上一点, 绕点A 逆时针旋转到 的位置.
(1)如图,旋转中心是 ,
(2)如图,如果M是AB 的中点,那么经过上述旋转后,点M转动了 ;
(3)如果点 D为 BC 边的三等分点,且. 的面积为 3,求四边形 ADCE 的面积.
11.如图,四边形 ABCD是正方形, 是等边三角形,M为对角线BD(不含 B、D点)上任意一点,将线段 BM绕点 B 逆时针旋转( °得到 BN,连接 EN、AM、CM.求证:
12.如图,△ABC中,点 E在BC 边上,AE=AB.将线段 AC绕点 A 旋转到 AF 的位置,使得∠CAF=∠BAE.连接 EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC 的度数.
13.在正方形 ABCD中,E是CD上的一点,
(1)如图1,将△ADE 绕点 A 顺时针方向旋转 90°,使 AD与AB 重合,得到△ABF,由旋转可知:DE= ,
∠AFB=∠
(2)如图2,正方形 ABCD中,P、Q分别是BC、CD边上一点,且∠PAQ=45°,试通过旋转的方法证明:DQ+BP=PQ;
(3)在(2)题中,连接 BD分别交AP、AQ于M、N,求证:
基础复习卷(一)23.1
1. D 2. A 3. C 4. A 5.10—2 6.60°或15° 7. B 8. A
9.(1)略 (2)(1,―4) (3)3.5 10.(1)点 A 60° (2)60° (3)9
11.证明:由旋转性质可知:BN=BM,∵△BAE为等边三角形,∴∠EBA=60°,BA=BE,
又 ∵ ∠MBN = 60°, ∴ ∠NBE = ∠MBA, 在 △ABM 和 △EBN
中
∴△ABM≌△EBN,∴AM=EN.
12.解:(1)证明:∵线段 AC绕点A 旋转到AF 的位置,∴AC=AF.
∵∠CAF=∠BAE, ∴ ∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.
在△ABC和△AEF中
∴△ABC≌△AEF(SAS),∴EF=BC.
(2)∵AF=AB,∴∠AEB=∠ABC=65°.
∴△ABC≌△AEF,∴∠AEF=∠ABC=65°,∠FEC=180°-∠AEB-∠AEF=180°-65°-65°=50°,
∵∠FGC是△EGC的外角,∠ACB=28°,∴∠FGC=∠FEC+∠ACB=50°+28°=78°.
13.(1)BF,AED;
(2)将△ADQ绕点A 按顺时针方向旋转90°,则AD与AB 重合,得到△ABE,如图,则∠D=∠ABE=90°,即点 E,B,P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,∴∠PAE=45°,∴∠PAQ=∠PAE,
在△APE和△APQ中,
PE=PQ,
而 PE=PB+BE=PB+DQ,∴DQ+BP=PQ;
(3)∵四边形 ABCD为正方形,∴∠ABD=∠ADB=45°,如图,将△ADN绕点 A 按顺时针方向旋转 90°,则 AD与 AB重合,得到△ABK,则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到 MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK 为直角三角形,
同课章节目录
