第二十三章 旋转 综合测试卷(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转 综合测试卷
(时间:100分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是 ( )
2.点A(3,2)关于原点的对称点 A′的坐标是 ( )
A.(-3,-2) B.(-2,-3) C.(3,2) D.(-3,2)
3.如图,△ABC与△A'B'C'关于O成中心对称,下列结论中不成立的是 ( )
4.如图,在方格纸上 是由 绕定点P顺时针旋转得到的.如果用(2,1)表示方格纸上A点的位置,(1,2)表示 B点的位置,那么点 P 的位置为 ( )
A.(5,2) B.(2,5) C.(2,1) D.(1,2)
5.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点 A 的对称点是点. 于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 ( )
A.3 B.2 C.6 D.5
6.如图,在△OAB 中,顶点 O(0,0),A(-3,4),B(3,4).将△OAB与正方形 ABCD 组成的图形绕点O顺时针旋转,每次旋转 则第 70次旋转结束时,点 D 的坐标为 ( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
7.如图所示,将正方形纸片 ABCD绕着点A 按逆时针方向旋转3 ’后得到正方形 若 则图中阴影部分的面积为 ( )
8.在平面直角坐标系中有三个点A(1,-1)、B(-1,-1)、C(0,1),点 P(0,2)关于 A 的对称点为 关于B 的 对称点为. 关于C 的对称点为. ,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到 P ,P ,P ,…,则点 . 的坐标是 ( )
A.(0,0) B.(0,2) C. (2,-4) D.(4,0)
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.如图,△ODC是由. 绕点 O 顺时针旋转! °后得到的图形,若点 D 恰好落在 AB 上,且∠AOC的度数为 130°,则∠C的度数是 .
10.如图,在直角坐标系中,已知点A(3,2),将 绕点O逆时针方向旋转 后得到△CDO,则点C的坐标是 .
11.如图,已知 AB=3,AC=1,∠D=90°,△DEC与 关于点C 成中心对称,则 AE 的长是 .
12.点 P(-4,3n+1)与 Q(2m,-7)关于原点对称,则
13.如图,在△ABC中,AB=AC=4,将 绕点 A 顺时针旋转 得到 延长AD交BC 的延长线于点E,则 DE的长为 .
14.已知正方形 ABCD中,点 E在DC 边上, ,如图,把线段 AE绕点 A 旋转,使点 E落在直线 BC 上的点 F 处,则 F、C两点间的距离为 .
三、解答题(本大题共6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
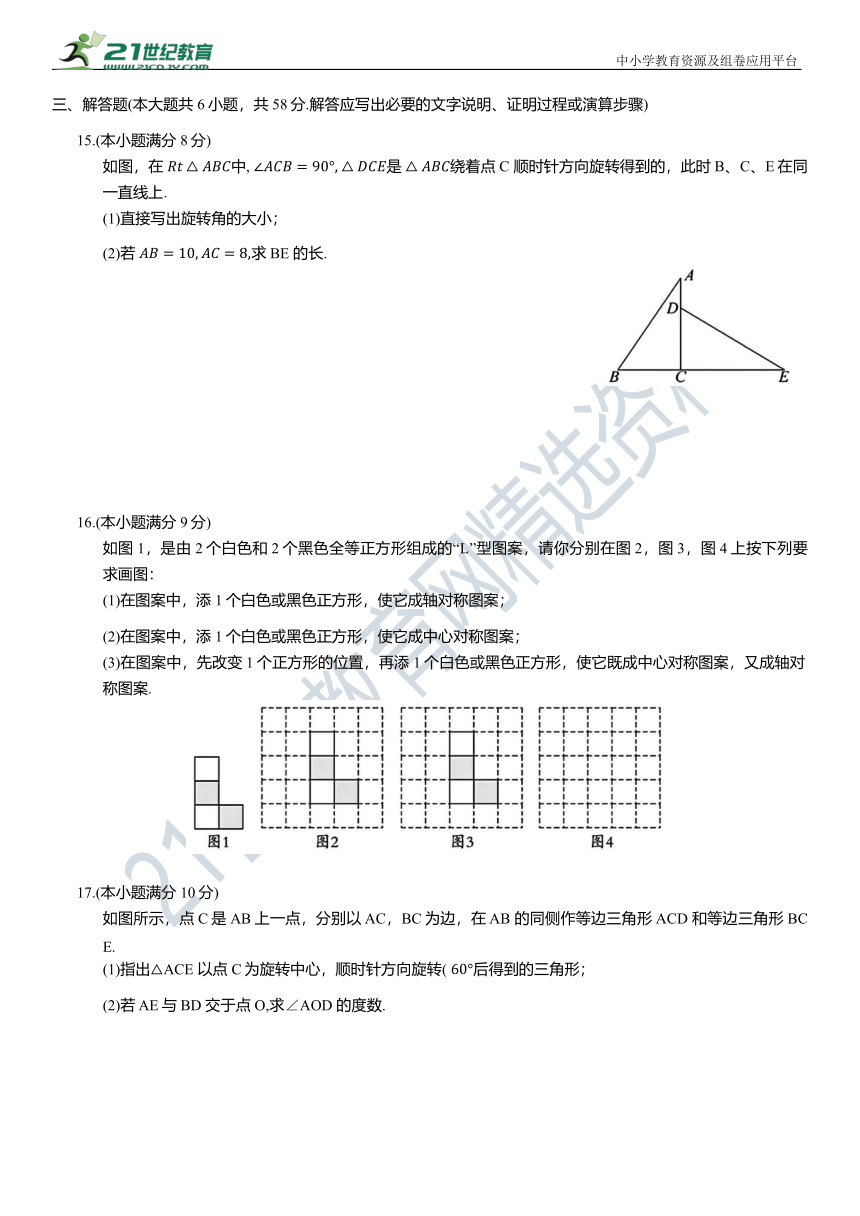
15.(本小题满分8分)
如图,在 中, 是 绕着点C 顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)直接写出旋转角的大小;
(2)若 求BE 的长.
16.(本小题满分9分)
如图1,是由2个白色和2个黑色全等正方形组成的“L”型图案,请你分别在图2,图3,图4上按下列要求画图:
(1)在图案中,添1个白色或黑色正方形,使它成轴对称图案;
(2)在图案中,添1个白色或黑色正方形,使它成中心对称图案;
(3)在图案中,先改变1个正方形的位置,再添 1个白色或黑色正方形,使它既成中心对称图案,又成轴对称图案.
17.(本小题满分 10分)
如图所示,点C是AB上一点,分别以 AC,BC为边,在 AB 的同侧作等边三角形ACD 和等边三角形BCE.
(1)指出△ACE 以点C为旋转中心,顺时针方向旋转( 后得到的三角形;
(2)若 AE与BD 交于点O,求∠AOD 的度数.
18.(本小题满分8分)
在平面直角坐标系中, 的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出 关于原点成中心对称的 ,并写出点 的坐标;
(2)画出将 绕点 按顺时针旋转 所得的
19.(本小题满分10分)
在 中, 将 绕点 C 顺时针旋转一个角度α得到 点A,B的对应点分别为 D,E.
(1)若点 E 恰好落在边 AC 上,如图1,求 的大小;
(2)若 ,F为AC 的中点,如图2,求证:四边形 BEDF 是平行四边形.
20.(本小题满分13分)
如图,点 E,F分别在正方形ABCD 的边CD,BC上,且. 点 P在射线BC上(点 P不与点 F 重合).将线段 EP绕点 E 顺时针旋转 得到线段 EG,过 E作GD 的垂线QH,垂足为 H,交射线 BC 于点Q.
(1)如图1,若点 E是CD 的中点,点 P在线段BF上,线段 BP,QC,EC的数量关系为 ;
(2)如图2,若点 E不是CD的中点,点 P在线段BF上,判断(1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由;
(3)正方形 ABCD的边长为 6, 请直接写出线段 BP的长.
第二十三章 综合测试卷
一、1. C 2. A 3. D 4. A 5. C 6. D 7. D 8. D
二、9.35° 10.(―3,―2) 11. 12.4 13.2 ―2 14.2或10
三、15.(1)旋转角为 90° (2)BE=14 16.略
17.(1)△ACE以点C为旋转中心,顺时针方向旋转( 后得到的三角形是△DCB.
(2)∠AOD=60°.
18.(1)图略 (2)图略
19.解:(1)在△ABC中, 由旋转性质得 DC=AC,∠DCE=∠ACB=30°.
又 =60°,
(2)证明:在△ABC中,
∵F是AC 的中点,
由旋转性质得
延长BF交EC于点G,则∠BGE=∠GBC+∠GCB=90°,∴∠BGE=∠DEC,∴DE∥BF,∴四边形 BEDF是平行四边形.
20.解:(1)BP+QC=EC.
(2)成立. 证明:根据题意得:∠PEG=90°,EP=EG,
∴∠PEQ+∠GEH=90°,
∵QH⊥GH,∴∠GHE=90°,∴∠EGH+∠GEH=90°,
∴∠PEQ=∠EGD,
∵四边形 ABCD是正方形,∴∠DCB=90°,BC=DC,
∴∠EPQ+∠PEC=90°,∵∠PEC+∠GED=90°,
∴∠GED=∠EPQ,又∵EG=PE,∠EGD=∠PEQ,∴△EGD≌△PEQ,∴DE=PQ,
∵CE=CD-DE,CD=BC,BP+QC=BC-PQ,∴BP+QC=EC.
其他证法参考图如下
(3)BP=3或BP=5
第二十三章 旋转 综合测试卷
(时间:100分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是 ( )
2.点A(3,2)关于原点的对称点 A′的坐标是 ( )
A.(-3,-2) B.(-2,-3) C.(3,2) D.(-3,2)
3.如图,△ABC与△A'B'C'关于O成中心对称,下列结论中不成立的是 ( )
4.如图,在方格纸上 是由 绕定点P顺时针旋转得到的.如果用(2,1)表示方格纸上A点的位置,(1,2)表示 B点的位置,那么点 P 的位置为 ( )
A.(5,2) B.(2,5) C.(2,1) D.(1,2)
5.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点 A 的对称点是点. 于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 ( )
A.3 B.2 C.6 D.5
6.如图,在△OAB 中,顶点 O(0,0),A(-3,4),B(3,4).将△OAB与正方形 ABCD 组成的图形绕点O顺时针旋转,每次旋转 则第 70次旋转结束时,点 D 的坐标为 ( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
7.如图所示,将正方形纸片 ABCD绕着点A 按逆时针方向旋转3 ’后得到正方形 若 则图中阴影部分的面积为 ( )
8.在平面直角坐标系中有三个点A(1,-1)、B(-1,-1)、C(0,1),点 P(0,2)关于 A 的对称点为 关于B 的 对称点为. 关于C 的对称点为. ,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到 P ,P ,P ,…,则点 . 的坐标是 ( )
A.(0,0) B.(0,2) C. (2,-4) D.(4,0)
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.如图,△ODC是由. 绕点 O 顺时针旋转! °后得到的图形,若点 D 恰好落在 AB 上,且∠AOC的度数为 130°,则∠C的度数是 .
10.如图,在直角坐标系中,已知点A(3,2),将 绕点O逆时针方向旋转 后得到△CDO,则点C的坐标是 .
11.如图,已知 AB=3,AC=1,∠D=90°,△DEC与 关于点C 成中心对称,则 AE 的长是 .
12.点 P(-4,3n+1)与 Q(2m,-7)关于原点对称,则
13.如图,在△ABC中,AB=AC=4,将 绕点 A 顺时针旋转 得到 延长AD交BC 的延长线于点E,则 DE的长为 .
14.已知正方形 ABCD中,点 E在DC 边上, ,如图,把线段 AE绕点 A 旋转,使点 E落在直线 BC 上的点 F 处,则 F、C两点间的距离为 .
三、解答题(本大题共6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分8分)
如图,在 中, 是 绕着点C 顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)直接写出旋转角的大小;
(2)若 求BE 的长.
16.(本小题满分9分)
如图1,是由2个白色和2个黑色全等正方形组成的“L”型图案,请你分别在图2,图3,图4上按下列要求画图:
(1)在图案中,添1个白色或黑色正方形,使它成轴对称图案;
(2)在图案中,添1个白色或黑色正方形,使它成中心对称图案;
(3)在图案中,先改变1个正方形的位置,再添 1个白色或黑色正方形,使它既成中心对称图案,又成轴对称图案.
17.(本小题满分 10分)
如图所示,点C是AB上一点,分别以 AC,BC为边,在 AB 的同侧作等边三角形ACD 和等边三角形BCE.
(1)指出△ACE 以点C为旋转中心,顺时针方向旋转( 后得到的三角形;
(2)若 AE与BD 交于点O,求∠AOD 的度数.
18.(本小题满分8分)
在平面直角坐标系中, 的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出 关于原点成中心对称的 ,并写出点 的坐标;
(2)画出将 绕点 按顺时针旋转 所得的
19.(本小题满分10分)
在 中, 将 绕点 C 顺时针旋转一个角度α得到 点A,B的对应点分别为 D,E.
(1)若点 E 恰好落在边 AC 上,如图1,求 的大小;
(2)若 ,F为AC 的中点,如图2,求证:四边形 BEDF 是平行四边形.
20.(本小题满分13分)
如图,点 E,F分别在正方形ABCD 的边CD,BC上,且. 点 P在射线BC上(点 P不与点 F 重合).将线段 EP绕点 E 顺时针旋转 得到线段 EG,过 E作GD 的垂线QH,垂足为 H,交射线 BC 于点Q.
(1)如图1,若点 E是CD 的中点,点 P在线段BF上,线段 BP,QC,EC的数量关系为 ;
(2)如图2,若点 E不是CD的中点,点 P在线段BF上,判断(1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由;
(3)正方形 ABCD的边长为 6, 请直接写出线段 BP的长.
第二十三章 综合测试卷
一、1. C 2. A 3. D 4. A 5. C 6. D 7. D 8. D
二、9.35° 10.(―3,―2) 11. 12.4 13.2 ―2 14.2或10
三、15.(1)旋转角为 90° (2)BE=14 16.略
17.(1)△ACE以点C为旋转中心,顺时针方向旋转( 后得到的三角形是△DCB.
(2)∠AOD=60°.
18.(1)图略 (2)图略
19.解:(1)在△ABC中, 由旋转性质得 DC=AC,∠DCE=∠ACB=30°.
又 =60°,
(2)证明:在△ABC中,
∵F是AC 的中点,
由旋转性质得
延长BF交EC于点G,则∠BGE=∠GBC+∠GCB=90°,∴∠BGE=∠DEC,∴DE∥BF,∴四边形 BEDF是平行四边形.
20.解:(1)BP+QC=EC.
(2)成立. 证明:根据题意得:∠PEG=90°,EP=EG,
∴∠PEQ+∠GEH=90°,
∵QH⊥GH,∴∠GHE=90°,∴∠EGH+∠GEH=90°,
∴∠PEQ=∠EGD,
∵四边形 ABCD是正方形,∴∠DCB=90°,BC=DC,
∴∠EPQ+∠PEC=90°,∵∠PEC+∠GED=90°,
∴∠GED=∠EPQ,又∵EG=PE,∠EGD=∠PEQ,∴△EGD≌△PEQ,∴DE=PQ,
∵CE=CD-DE,CD=BC,BP+QC=BC-PQ,∴BP+QC=EC.
其他证法参考图如下
(3)BP=3或BP=5
同课章节目录
