24.4弧长和扇形面积 同步练习(无答案) 人教版数学九年级 上册
文档属性
| 名称 | 24.4弧长和扇形面积 同步练习(无答案) 人教版数学九年级 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 339.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 08:36:53 | ||
图片预览


文档简介
24.4弧长和扇形面积
一、选择题。
1.圆锥的底面圆半径是1,母线长是3,它的侧面展开图的圆心角是( )
A.90° B.100° C.120° D.150°
2.若圆锥的底面直径为4cm,侧面展开图的面积为6πcm2,则圆锥的母线长为( )
A. B. C.3cm D.2cm
3.一条弧所对的圆心角是144°,那么这条弧长与这条弧所在圆的周长之比为( )
A. B. C. D.
4.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
5.如图,AB是⊙O的直径,AC是⊙O的弦,若∠A=20°,AB=6,则弧长为( )
A. B. C. D.
6.如图,圆锥底面圆的半径AB=4,母线长AC=12,则这个圆锥的侧面积为( )
A.16π B.24π C.48π D.96π
7.一个垃圾填埋场,它在地面上的形状为长80m,宽60m的矩形,有污水从该矩形的四周边界向外渗透了3m,则该垃圾填埋场外围受污染土地的面积为( )
A.(840+6π)m2 B.(840+9π)m2 C.840m2 D.876m2
8.如图,在△ABC中,AB=AC,∠C=30°,AC=4,以AB为直径的⊙O交BC于点D,则图中阴影部分的面积为( )
A. B. C. D.2π
9.将一张正方形的透明纸片ABCD和⊙O按如图位置叠放,顶点A、D在⊙O上,边AB、BC、CD分别与⊙O相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B. C. D.
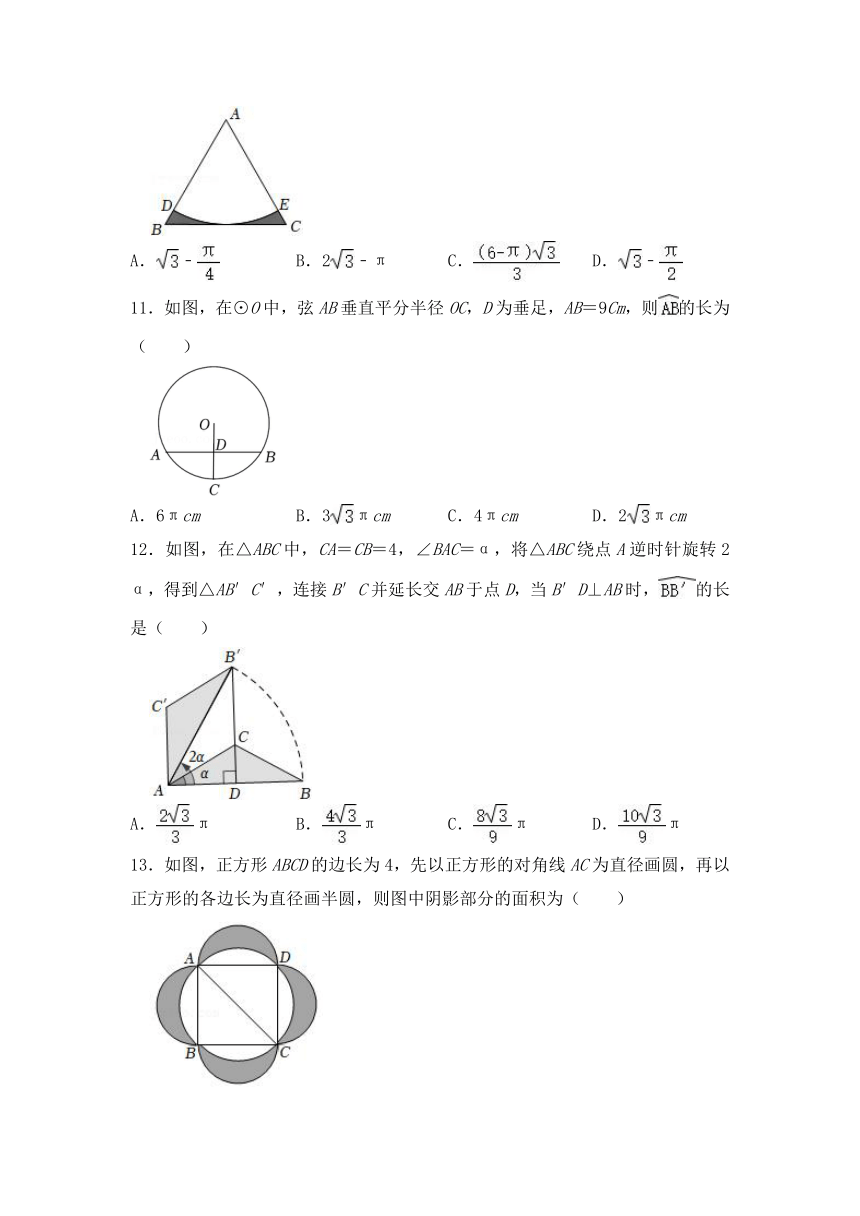
10.如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A.﹣ B.2﹣π C. D.﹣
11.如图,在⊙O中,弦AB垂直平分半径OC,D为垂足,AB=9Cm,则的长为( )
A.6πcm B.3πcm C.4πcm D.2πcm
12.如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB′C′,连接B′C并延长交AB于点D,当B′D⊥AB时,的长是( )
A.π B.π C.π D.π
13.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
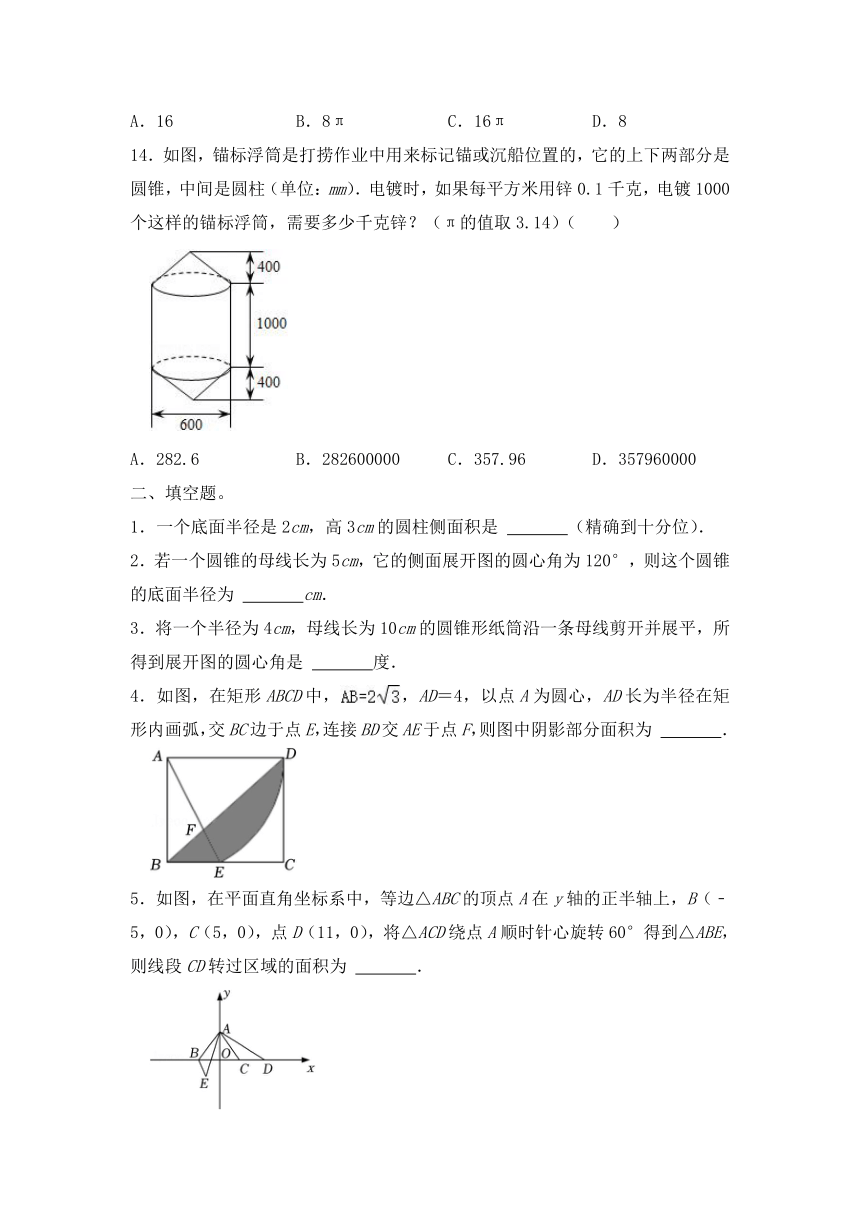
14.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A.282.6 B.282600000 C.357.96 D.357960000
二、填空题。
1.一个底面半径是2cm,高3cm的圆柱侧面积是 (精确到十分位).
2.若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为 cm.
3.将一个半径为4cm,母线长为10cm的圆锥形纸筒沿一条母线剪开并展平,所得到展开图的圆心角是 度.
4.如图,在矩形ABCD中,,AD=4,以点A为圆心,AD长为半径在矩形内画弧,交BC边于点E,连接BD交AE于点F,则图中阴影部分面积为 .
5.如图,在平面直角坐标系中,等边△ABC的顶点A在y轴的正半轴上,B(﹣5,0),C(5,0),点D(11,0),将△ACD绕点A顺时针心旋转60°得到△ABE,则线段CD转过区域的面积为 .
6.如图,将半径为2,圆心角为90°的扇形ABC绕A点逆时针旋转,点B的对应点点D落在弧AC上,则阴影部分的面积为 .
7.如图,在△ABC中,AB=AC,∠A=50°,以AB为直径的⊙O交边BC,AC于D,E两点,AC=2,则的长是 .
三、解答题。
1.如图,⊙O的内接四边形ABCD两组对边的延长线分别相交于点E,F,∠E=∠F.
(1)求证:AC是直径;
(2)若⊙O的半径为1,∠E=40°,求的长度.
2.如图,在△ABC中,AB=AC.以BC为直径画圆O分别交AB,AC于点D,E.
(1)求证:BD=CE;
(2)当△ABC中,∠B=70°且BC=12时,求的长.
3.如图,在△ABC中,AB=AC=26,以腰AB为直径作半圆,分别交BC、AC于
点D、E.
(1)若∠BAC=50°,求弧BE的长.
(2)连结DE,求证:BD=DE.
4.如图,A,B,C是⊙O上三点,其中=2,过点B画BD⊥OC于点D.
(1)求证:AB=2BD;
(2)若AB=4,CD=2,求图中阴影部分的面积.
5.如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).
6.如图,已知四边形ABCD是⊙O的内接四边形,∠BCD=90°,连接AC,BD,作∠DAE=∠ACB,AE交CD的延长线于点E.
(1)求证:AE∥BD;
(2)若,CD=2DE,⊙O的半径为r,求劣弧的长.(用含r的代数式表示)
7.如图,已知AD是⊙O的直径,B、C为圆上的点,OE⊥AB、BC⊥AD,垂足分别为E、F.
(1)求证:2OE=CD;
(2)若∠BAD+∠EOF=150°,AD=4,求阴影部分的面积.
一、选择题。
1.圆锥的底面圆半径是1,母线长是3,它的侧面展开图的圆心角是( )
A.90° B.100° C.120° D.150°
2.若圆锥的底面直径为4cm,侧面展开图的面积为6πcm2,则圆锥的母线长为( )
A. B. C.3cm D.2cm
3.一条弧所对的圆心角是144°,那么这条弧长与这条弧所在圆的周长之比为( )
A. B. C. D.
4.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2π B.2 C.2π﹣4 D.2π﹣2
5.如图,AB是⊙O的直径,AC是⊙O的弦,若∠A=20°,AB=6,则弧长为( )
A. B. C. D.
6.如图,圆锥底面圆的半径AB=4,母线长AC=12,则这个圆锥的侧面积为( )
A.16π B.24π C.48π D.96π
7.一个垃圾填埋场,它在地面上的形状为长80m,宽60m的矩形,有污水从该矩形的四周边界向外渗透了3m,则该垃圾填埋场外围受污染土地的面积为( )
A.(840+6π)m2 B.(840+9π)m2 C.840m2 D.876m2
8.如图,在△ABC中,AB=AC,∠C=30°,AC=4,以AB为直径的⊙O交BC于点D,则图中阴影部分的面积为( )
A. B. C. D.2π
9.将一张正方形的透明纸片ABCD和⊙O按如图位置叠放,顶点A、D在⊙O上,边AB、BC、CD分别与⊙O相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B. C. D.
10.如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A.﹣ B.2﹣π C. D.﹣
11.如图,在⊙O中,弦AB垂直平分半径OC,D为垂足,AB=9Cm,则的长为( )
A.6πcm B.3πcm C.4πcm D.2πcm
12.如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB′C′,连接B′C并延长交AB于点D,当B′D⊥AB时,的长是( )
A.π B.π C.π D.π
13.如图,正方形ABCD的边长为4,先以正方形的对角线AC为直径画圆,再以正方形的各边长为直径画半圆,则图中阴影部分的面积为( )
A.16 B.8π C.16π D.8
14.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A.282.6 B.282600000 C.357.96 D.357960000
二、填空题。
1.一个底面半径是2cm,高3cm的圆柱侧面积是 (精确到十分位).
2.若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为 cm.
3.将一个半径为4cm,母线长为10cm的圆锥形纸筒沿一条母线剪开并展平,所得到展开图的圆心角是 度.
4.如图,在矩形ABCD中,,AD=4,以点A为圆心,AD长为半径在矩形内画弧,交BC边于点E,连接BD交AE于点F,则图中阴影部分面积为 .
5.如图,在平面直角坐标系中,等边△ABC的顶点A在y轴的正半轴上,B(﹣5,0),C(5,0),点D(11,0),将△ACD绕点A顺时针心旋转60°得到△ABE,则线段CD转过区域的面积为 .
6.如图,将半径为2,圆心角为90°的扇形ABC绕A点逆时针旋转,点B的对应点点D落在弧AC上,则阴影部分的面积为 .
7.如图,在△ABC中,AB=AC,∠A=50°,以AB为直径的⊙O交边BC,AC于D,E两点,AC=2,则的长是 .
三、解答题。
1.如图,⊙O的内接四边形ABCD两组对边的延长线分别相交于点E,F,∠E=∠F.
(1)求证:AC是直径;
(2)若⊙O的半径为1,∠E=40°,求的长度.
2.如图,在△ABC中,AB=AC.以BC为直径画圆O分别交AB,AC于点D,E.
(1)求证:BD=CE;
(2)当△ABC中,∠B=70°且BC=12时,求的长.
3.如图,在△ABC中,AB=AC=26,以腰AB为直径作半圆,分别交BC、AC于
点D、E.
(1)若∠BAC=50°,求弧BE的长.
(2)连结DE,求证:BD=DE.
4.如图,A,B,C是⊙O上三点,其中=2,过点B画BD⊥OC于点D.
(1)求证:AB=2BD;
(2)若AB=4,CD=2,求图中阴影部分的面积.
5.如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).
6.如图,已知四边形ABCD是⊙O的内接四边形,∠BCD=90°,连接AC,BD,作∠DAE=∠ACB,AE交CD的延长线于点E.
(1)求证:AE∥BD;
(2)若,CD=2DE,⊙O的半径为r,求劣弧的长.(用含r的代数式表示)
7.如图,已知AD是⊙O的直径,B、C为圆上的点,OE⊥AB、BC⊥AD,垂足分别为E、F.
(1)求证:2OE=CD;
(2)若∠BAD+∠EOF=150°,AD=4,求阴影部分的面积.
同课章节目录
