4.3 实数(第1课时)课件(共29张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 4.3 实数(第1课时)课件(共29张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 21:31:55 | ||
图片预览




文档简介
第4章 · 平方根
4.3 实数(1)
第1课时 实数及其分类
学习目标
1. 了解实数的概念,能对实数按要求进行分类;
2. 会判断一个数是无理数还是有理数;
3. 知道实数和数轴上的点是一一对应的关系;
4. 体会“数形结合”的数学思想.
知识回顾
在七年级我们学习了无理数——
无限不循环小数.
你能画出长度为无理数的线段吗?
小组讨论、交流,说说自己的想法.
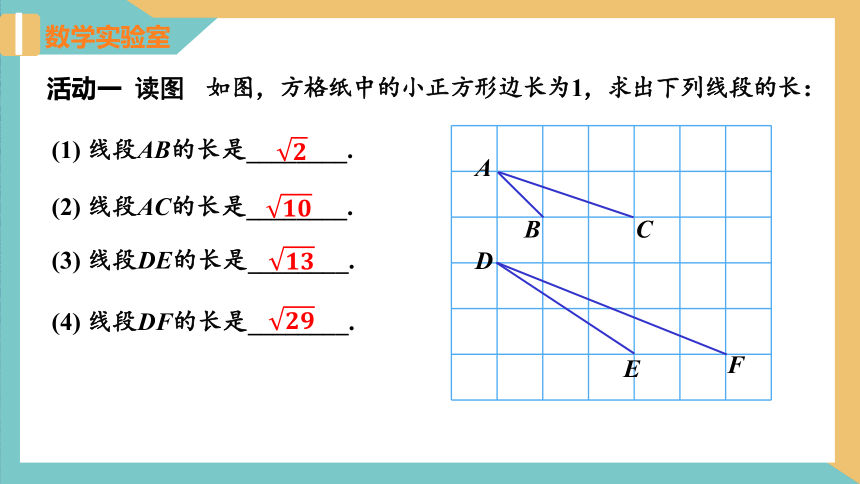
活动一 读图
数学实验室
(1) 线段AB的长是________.
(2) 线段AC的长是________.
(3) 线段DE的长是________.
(4) 线段DF的长是________.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
D
E
F
????
?
????????
?
????????
?
????????
?
如图,方格纸中的小正方形边长为1,求出下列线段的长:
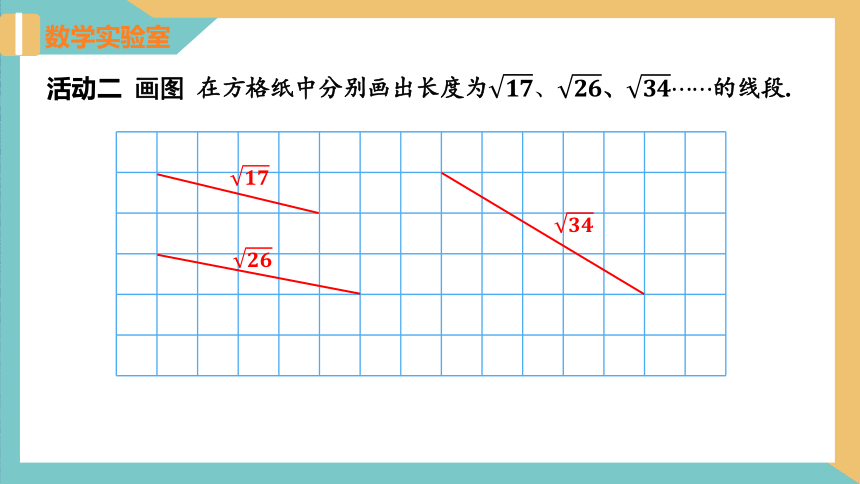
在方格纸中分别画出长度为????????、????????、??????????的线段.
?
数学实验室
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????????
?
????????
?
????????
?
活动二 画图
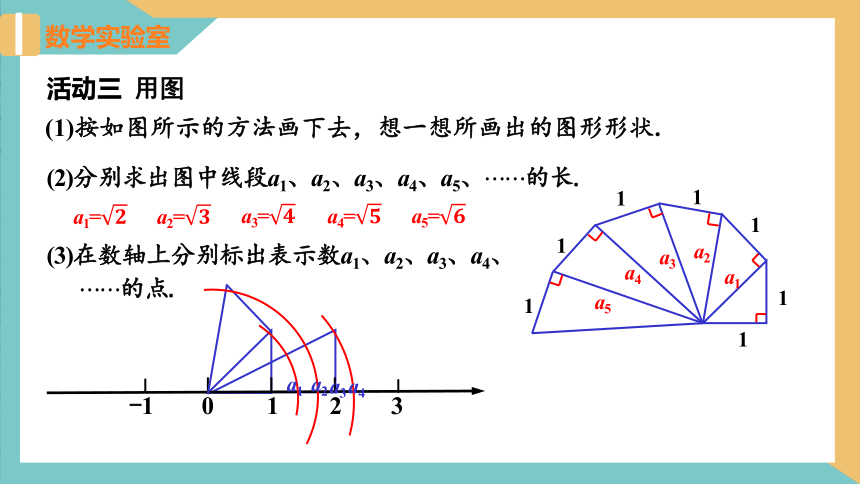
(1)按如图所示的方法画下去,想一想所画出的图形形状.
数学实验室
活动三 用图
(2)分别求出图中线段a1、a2、a3、a4、a5、??的长.
?
a1
1
1
1
1
1
1
1
a2
a3
a4
a5
a1=????
?
a2=????
?
a3=????
?
a4=????
?
a5=????
?
(3)在数轴上分别标出表示数a1、a2、a3、a4、
??的点.
?
0
1
-1
2
3
a2
a3
a4
a1
探索与交流
除了像这样带根号的无理数外,你还能写出别的形式的无理数吗?
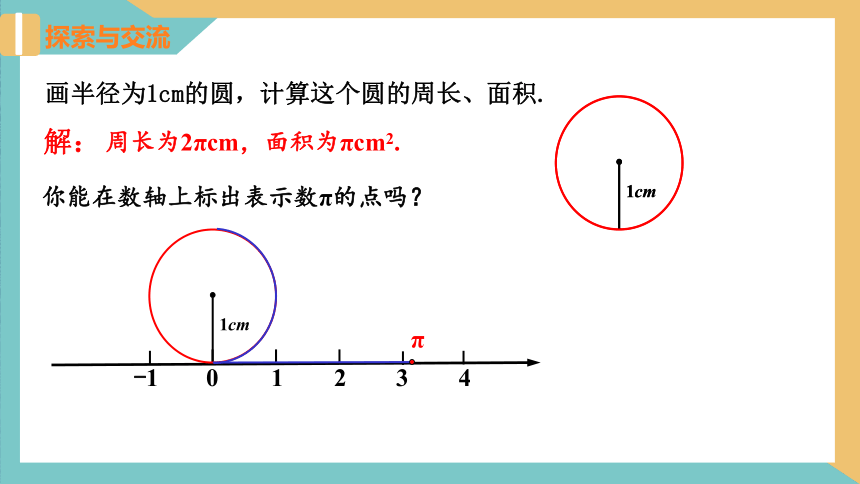
画半径为1cm的圆,计算这个圆的周长、面积.
解:
周长为2πcm,面积为πcm2.
你能在数轴上标出表示数π的点吗?
0
1
-1
2
3
4
1cm
1cm
1cm
π
像???? 、????、????、????、????????、????????、π、2π等,这些数都是无理数.
?
有理数都可以用数轴上的点来表示;
反过来,数轴上的点是否都表示有理数?
无理数也可以用数轴上的点来表示.
探索与交流
反过来,数轴上的点是否都表示无理数?
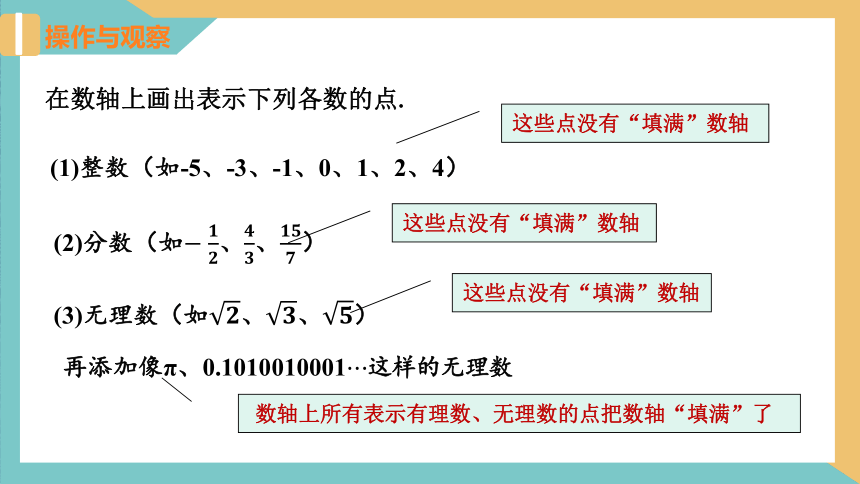
操作与观察
在数轴上画出表示下列各数的点.
(1)整数(如-5、-3、-1、0、1、2、4)
这些点没有“填满”数轴
(2)分数(如?????????、????????、????????????)
?
这些点没有“填满”数轴
(3)无理数(如????、????、????)
?
这些点没有“填满”数轴
再添加像π、0.1010010001?这样的无理数
?
数轴上所有表示有理数、无理数的点把数轴“填满”了
实数的概念:
概念学习
有理数和无理数统称为实数.
即实数可分为有理数和无理数.
每一个实数都可以用数轴上的一个点来表示;反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的.
讨论:到目前为止,同学们知道的数有哪些类?你能给它们分类吗?
新知归纳
实数的分类:
(按定义)
实数
有理数
无理数
整数
零
分数
正无理数
负无理数
正整数
负整数
正分数
负分数
有限小数或无限循环小数
无限不循环小数
自然数
新知归纳
实数的分类:
(按正负)
实数
正实数
负实数
正有理数
零
负有理数
正无理数
负无理数
正整数
正分数
负整数
负分数
例题讲解
例1 将下列各数填入相应的括号内:
3,-3,0,????????,-????????,????,-????,????????,????????,π,????????,????????.
?
有理数:?????????????????????????????????????????????????????????????????????;
无理数:?????????????????????????????????????????????????????????????????????;
正整数:?????????????????????????????????????????????????????????????????????;
分数:??????????????????????????????????????????????????????????????????????????.
?
????,?????,????,????????,?????????,????????,?
?
????,?????,??????,????,????????,????????,?
?
????,????????,?
?
????????,?????????,…
?
先化简,后判断
方法总结
判断无理数的方法:
无理数是无限不循环小数,其类型主要有三种:
①根号型:含有根号且被开方数不能被开尽的式子,如????;
②含 π 型:化简后含π的数,如π,????????等;
③构造型:具有某些特殊结构的小数,如0.1010010001 ? .
另外,注意带根号的数不一定是无理数,如????,要先化简,后判断.
无理数也不一定带根号,如π.
?
例2 在数轴上找出表示????的点. (不写作法,保留作图痕迹)
?
例题讲解
0
1
-1
2
3
????
?
解:如图所示.
根据勾股定理,将带根号的数看成是直角边长为整数的直角三角形的斜边长,利用数轴画出这个三角形,再运用圆规将相应线段转移到数轴相应的位置上.
方法总结
根据勾股定理在数轴上表示无理数的方法:
新知巩固
(1)无理数都是开方开不尽的数.( )(2)无理数都是无限小数.( )(3)无限小数都是无理数.( )(4)无理数包括正无理数、零、负无理数.( ) (5)不带根号的数都是有理数.( )(6)带根号的数都是无理数.( )(7)有理数都是有限小数.( )(8)实数包括有限小数和无限小数.( )
1. 判断正误,在后面的括号里对的填写“正确”,错的填写“错误”,并说明理由.
√
×
×
×
×
×
×
√
新知巩固
正数:{ …};
负数:{ …};
有理数:{ …};
无理数:{ …}.
3. 把下列各数填入相应的括号内:
-????????,????????????,0.1,????????,????????,?????????,0,0.1212212221? .
?
????????????,????.????,????????,????????,????.?????????????????????????????????????????
?
?????????,?????????,
?
?????????,????.????,????????,?????????,????,
?
????????????,????????,????.?????????????????????????????????????????
?
4. 在数轴上作出表示-????????的点.
?
新知巩固
解:如图所示.
-4
-3
-5
-2
-1
0
1
?????????
?
课堂小结
实数
概念与分类
与数轴上点的关系
按定义
按正负
一一对应
当堂检测
1. 下列说法正确的是( )
A.无理数都是无限小数 B.无限小数都是无理数
C.带根号的数都是无理数 D.无理数与数轴上的点是一一对应的
A
2. 和数轴上的点一一对应的是 ( )
A.整数 B.有理数 C.无理数 D.实数
D
新知巩固
4. 下列各数中无理数有 ( )
3.141,-????????????,????,????????????,π,0,4.2????????··,0.1010010001??
A. 2个 B. 3个 C. 4个 D. 5个
?
3.关于????,下列说法正确的是( )A.是整数 B.是分数 C.是有理数 D.是无理数
?
D
B
当堂检测
5. 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合.将圆沿数轴滚动1周,点A到达点B的位置,则点B表示的数是(?? ? ?)
A. π-1 B.-π-1 C.-π+1 D. π-1或-π-1
-4
-3
-5
-2
-1
0
1
A
D
当堂检测
6.实数????????????,????,-8,????????,????????,????????中的无理数是 .?
?
????,????????,????????
?
7.写出一个大于0而小于1的无理数: ___________ .?
如????????,答案不唯一
?
8.如图,数轴上的点A和点B之间的整数点为________________.
-1,0,1,2
当堂检测
9.如图,矩形ABCD的边长AD为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则点E表示的实数是____________.
????-1
?
当堂检测
(1)有理数集合:{_______________________…};
(2)负无理数集合:{_____________________…};
(3)正实数集合:{________________…}.
????????,????????,-????????,?????????,0,-0.????????,1.414,?????.
?
10. 把下列各数分别填入相应的集合里:
????????,
?
?????????,
?
0,
-0.????????,
?
1.414
-????????,
?
?????
?
????????,
?
????????,
?
1.414
当堂检测
11.如图,在3×3的正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
(1)请在网格图中作一个三边长分别为3,????,????的三角形;
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
当堂检测
11.如图,在3×3的正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)画一个三边长均为无理数的等腰直角三角形(不要求证明), 并求出其面积.
当堂检测
12.如图,细心观察,认真分析各式,然后解答下列问题:(????)????+1=2,S1=????????;(????)????+1=3,S2=????????;(????)????+1=4,S3=????????;??
?
(1)OA10的长为________;
????????
?
(2)请用含有n(n是正整数)的等式表示上述变化规律;
解:OAn=????,????????=?????????????=????????.
4.3 实数(1)
第1课时 实数及其分类
学习目标
1. 了解实数的概念,能对实数按要求进行分类;
2. 会判断一个数是无理数还是有理数;
3. 知道实数和数轴上的点是一一对应的关系;
4. 体会“数形结合”的数学思想.
知识回顾
在七年级我们学习了无理数——
无限不循环小数.
你能画出长度为无理数的线段吗?
小组讨论、交流,说说自己的想法.
活动一 读图
数学实验室
(1) 线段AB的长是________.
(2) 线段AC的长是________.
(3) 线段DE的长是________.
(4) 线段DF的长是________.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
D
E
F
????
?
????????
?
????????
?
????????
?
如图,方格纸中的小正方形边长为1,求出下列线段的长:
在方格纸中分别画出长度为????????、????????、??????????的线段.
?
数学实验室
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????????
?
????????
?
????????
?
活动二 画图
(1)按如图所示的方法画下去,想一想所画出的图形形状.
数学实验室
活动三 用图
(2)分别求出图中线段a1、a2、a3、a4、a5、??的长.
?
a1
1
1
1
1
1
1
1
a2
a3
a4
a5
a1=????
?
a2=????
?
a3=????
?
a4=????
?
a5=????
?
(3)在数轴上分别标出表示数a1、a2、a3、a4、
??的点.
?
0
1
-1
2
3
a2
a3
a4
a1
探索与交流
除了像这样带根号的无理数外,你还能写出别的形式的无理数吗?
画半径为1cm的圆,计算这个圆的周长、面积.
解:
周长为2πcm,面积为πcm2.
你能在数轴上标出表示数π的点吗?
0
1
-1
2
3
4
1cm
1cm
1cm
π
像???? 、????、????、????、????????、????????、π、2π等,这些数都是无理数.
?
有理数都可以用数轴上的点来表示;
反过来,数轴上的点是否都表示有理数?
无理数也可以用数轴上的点来表示.
探索与交流
反过来,数轴上的点是否都表示无理数?
操作与观察
在数轴上画出表示下列各数的点.
(1)整数(如-5、-3、-1、0、1、2、4)
这些点没有“填满”数轴
(2)分数(如?????????、????????、????????????)
?
这些点没有“填满”数轴
(3)无理数(如????、????、????)
?
这些点没有“填满”数轴
再添加像π、0.1010010001?这样的无理数
?
数轴上所有表示有理数、无理数的点把数轴“填满”了
实数的概念:
概念学习
有理数和无理数统称为实数.
即实数可分为有理数和无理数.
每一个实数都可以用数轴上的一个点来表示;反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的.
讨论:到目前为止,同学们知道的数有哪些类?你能给它们分类吗?
新知归纳
实数的分类:
(按定义)
实数
有理数
无理数
整数
零
分数
正无理数
负无理数
正整数
负整数
正分数
负分数
有限小数或无限循环小数
无限不循环小数
自然数
新知归纳
实数的分类:
(按正负)
实数
正实数
负实数
正有理数
零
负有理数
正无理数
负无理数
正整数
正分数
负整数
负分数
例题讲解
例1 将下列各数填入相应的括号内:
3,-3,0,????????,-????????,????,-????,????????,????????,π,????????,????????.
?
有理数:?????????????????????????????????????????????????????????????????????;
无理数:?????????????????????????????????????????????????????????????????????;
正整数:?????????????????????????????????????????????????????????????????????;
分数:??????????????????????????????????????????????????????????????????????????.
?
????,?????,????,????????,?????????,????????,?
?
????,?????,??????,????,????????,????????,?
?
????,????????,?
?
????????,?????????,…
?
先化简,后判断
方法总结
判断无理数的方法:
无理数是无限不循环小数,其类型主要有三种:
①根号型:含有根号且被开方数不能被开尽的式子,如????;
②含 π 型:化简后含π的数,如π,????????等;
③构造型:具有某些特殊结构的小数,如0.1010010001 ? .
另外,注意带根号的数不一定是无理数,如????,要先化简,后判断.
无理数也不一定带根号,如π.
?
例2 在数轴上找出表示????的点. (不写作法,保留作图痕迹)
?
例题讲解
0
1
-1
2
3
????
?
解:如图所示.
根据勾股定理,将带根号的数看成是直角边长为整数的直角三角形的斜边长,利用数轴画出这个三角形,再运用圆规将相应线段转移到数轴相应的位置上.
方法总结
根据勾股定理在数轴上表示无理数的方法:
新知巩固
(1)无理数都是开方开不尽的数.( )(2)无理数都是无限小数.( )(3)无限小数都是无理数.( )(4)无理数包括正无理数、零、负无理数.( ) (5)不带根号的数都是有理数.( )(6)带根号的数都是无理数.( )(7)有理数都是有限小数.( )(8)实数包括有限小数和无限小数.( )
1. 判断正误,在后面的括号里对的填写“正确”,错的填写“错误”,并说明理由.
√
×
×
×
×
×
×
√
新知巩固
正数:{ …};
负数:{ …};
有理数:{ …};
无理数:{ …}.
3. 把下列各数填入相应的括号内:
-????????,????????????,0.1,????????,????????,?????????,0,0.1212212221? .
?
????????????,????.????,????????,????????,????.?????????????????????????????????????????
?
?????????,?????????,
?
?????????,????.????,????????,?????????,????,
?
????????????,????????,????.?????????????????????????????????????????
?
4. 在数轴上作出表示-????????的点.
?
新知巩固
解:如图所示.
-4
-3
-5
-2
-1
0
1
?????????
?
课堂小结
实数
概念与分类
与数轴上点的关系
按定义
按正负
一一对应
当堂检测
1. 下列说法正确的是( )
A.无理数都是无限小数 B.无限小数都是无理数
C.带根号的数都是无理数 D.无理数与数轴上的点是一一对应的
A
2. 和数轴上的点一一对应的是 ( )
A.整数 B.有理数 C.无理数 D.实数
D
新知巩固
4. 下列各数中无理数有 ( )
3.141,-????????????,????,????????????,π,0,4.2????????··,0.1010010001??
A. 2个 B. 3个 C. 4个 D. 5个
?
3.关于????,下列说法正确的是( )A.是整数 B.是分数 C.是有理数 D.是无理数
?
D
B
当堂检测
5. 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合.将圆沿数轴滚动1周,点A到达点B的位置,则点B表示的数是(?? ? ?)
A. π-1 B.-π-1 C.-π+1 D. π-1或-π-1
-4
-3
-5
-2
-1
0
1
A
D
当堂检测
6.实数????????????,????,-8,????????,????????,????????中的无理数是 .?
?
????,????????,????????
?
7.写出一个大于0而小于1的无理数: ___________ .?
如????????,答案不唯一
?
8.如图,数轴上的点A和点B之间的整数点为________________.
-1,0,1,2
当堂检测
9.如图,矩形ABCD的边长AD为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则点E表示的实数是____________.
????-1
?
当堂检测
(1)有理数集合:{_______________________…};
(2)负无理数集合:{_____________________…};
(3)正实数集合:{________________…}.
????????,????????,-????????,?????????,0,-0.????????,1.414,?????.
?
10. 把下列各数分别填入相应的集合里:
????????,
?
?????????,
?
0,
-0.????????,
?
1.414
-????????,
?
?????
?
????????,
?
????????,
?
1.414
当堂检测
11.如图,在3×3的正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
(1)请在网格图中作一个三边长分别为3,????,????的三角形;
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
当堂检测
11.如图,在3×3的正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)画一个三边长均为无理数的等腰直角三角形(不要求证明), 并求出其面积.
当堂检测
12.如图,细心观察,认真分析各式,然后解答下列问题:(????)????+1=2,S1=????????;(????)????+1=3,S2=????????;(????)????+1=4,S3=????????;??
?
(1)OA10的长为________;
????????
?
(2)请用含有n(n是正整数)的等式表示上述变化规律;
解:OAn=????,????????=?????????????=????????.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
