几何类探索题--变中寻不变
图片预览

文档简介
几何类探索题——变中寻不变
几何中创新发展的思维策略,是新的(或条件,或图形的)变化将各种思维方法灵活应用,产生新思路的思维策略,是将创新精神,创新思维,创新技法综合使用,促进发展的思维策略。
几何中,在图形的多样变换下,解决问题。为培养学生的创新思维的发展提供了广阔的空间。下面,我们就几何中与图形变换有关的问题,从创新思维方法和技法两个方面,对与图形变换有关的问题作初步的探索。
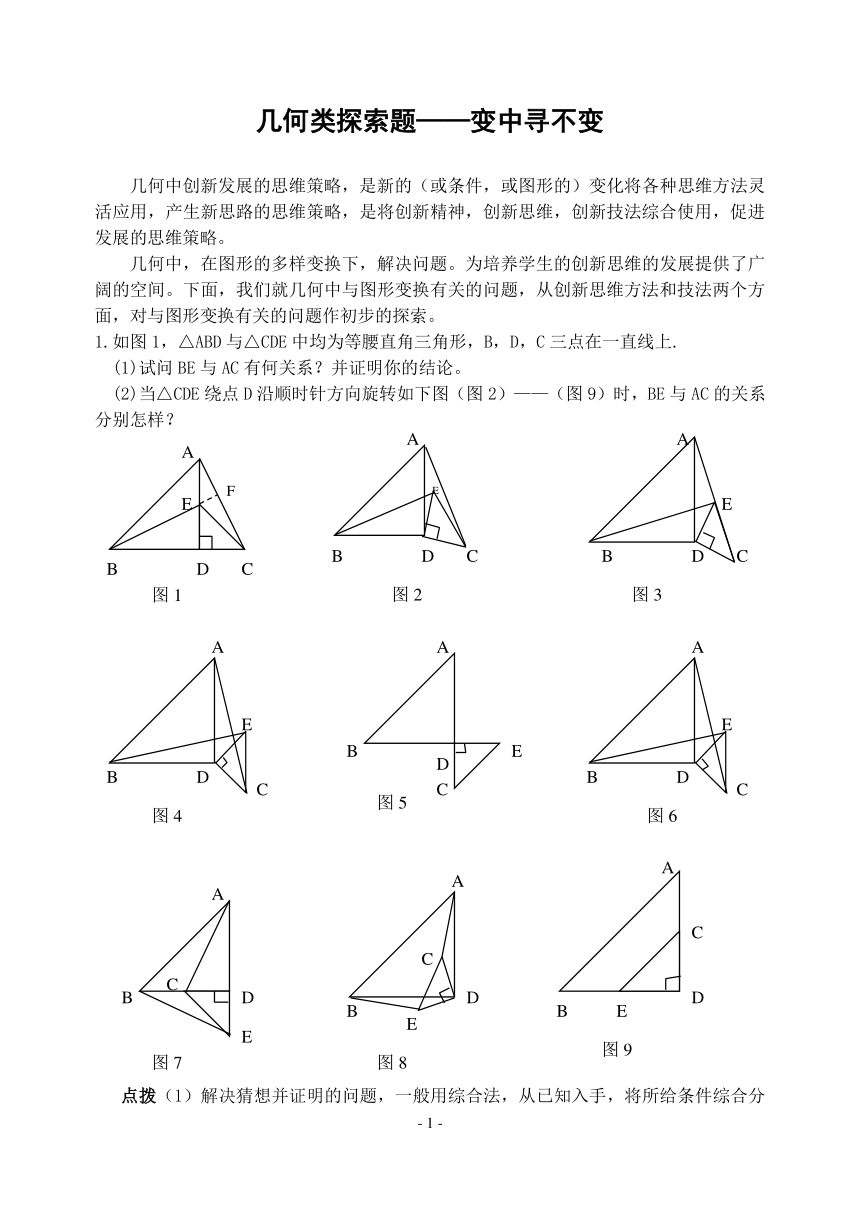
1.如图1,△ABD与△CDE中均为等腰直角三角形,B,D,C三点在一直线上.
(1)试问BE与AC有何关系?并证明你的结论。
(2)当△CDE绕点D沿顺时针方向旋转如下图(图2)——(图9)时,BE与AC的关系分别怎样?
点拨(1)解决猜想并证明的问题,一般用综合法,从已知入手,将所给条件综合分析。本题中条件,△ABD与△CDE中均为等腰直角三角形,可得,AD=BD,∠ADB=∠EDC,ED=DC,所以△BDE≌△ADC,又因为几何中,判断两个量的关系,要考虑位置关系和数量关系,所以猜想:BE=AC,BE⊥AC。
答:(1)BE=AC,BE⊥AC
证明:延长BE交AC于F,
∵△ABD与△CDE中均为等腰直角三角形
在△BDE与中△ADC中:
∵AD=BD,∠ADB=∠EDC,ED=DC
∴△BDE≌△ADC
∴BE=AC,∠EAF=∠EBD,
∴∠EAF+∠AEF =∠EBD+∠BED=90°
∴∠AFE=90°即BE⊥AC
(2)(图2)——(图9)时,BE与AC的关系不变。
点拨:解这类题要特别注意图形的变化,从图形的变化中把握本质,找出某些固定不变的关系,即“变中寻不变”。猜想其规律,再运用几何知识加以证明。(其解题关键是“变中寻不变”。)本题图形位置虽然发生了几多变化,但本题本质上△BDE≌△ADC不变,(即变中的不变关系是△BDE≌△ADC,)其他位置时,同理(用“边角边”)可证得结论。图5,图9,可根据图直接求得。
2.已知:等边△ABC和点P,设点P到△ABC的三边AB,AC,BC的距离为h1,h2,h3,△ABC的高为h,“若点P在一边BC上,(如图1)此时h3=0,可得结论:h1+h2+h3=h”。请直接应用上述信息.解决下列问题:
当点P在△ABC内,(如图2),点P在△ABC外,(如图3),这两种情况时,上述结论是否成立?若成立,请给予证明;若不成立h1,h2,h3 与 h之间又有怎样的关系?请写出你的猜想,不需证明。
点拨:已知中“若点P在一边BC上,(如图1)此时h=0,可得结论:h1+h2+h3=h”的证明思路,连接AP,由S= S+S,即BC·AM=AB·PD+AC·PE,可得h1+h2+h3=h 。
(1)中,当点P在△ABC内时,点P的位置,及h1,h2,h3的大小发生变化,但是本题S的大小没有改变(即变中的不变关系是,S的大小不变),所以依然用S= S+S+S的关系即可证得结论。
(1) 当点P在△ABC内时,如图3,结论h1+h2+h3=h仍然成立。
证明:连接PA,PB,PC.
∵△ABC是等边三角形,∴AB=BC=AC.
∵AM⊥BC,∴S=BC·AM.
∵PD⊥AB,PE⊥AC,PF⊥BC.
∴S=AB·PD ,S=AC·PE ,S=BC·PF.
S= S+S+S.
∴BC·AM=AB·PD+AC·PE+BC·PF.
∴AM=PD+PE+PF,∴h1+h2+h3=h.
(2) 当P点在△ABC外部时,h1+h2+h3=h 不成立,此时h1+h2+h3=h.
点拨:(2)当P点在△ABC外部时,S= S+S - S,
即BC·AM=AB·PD+AC·PE - BC·PF,
所以h1+h2-h3=h.
同类练习:
如图1,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,求证:BD平分EF,
想一想 上题中,若将△DEC的边EC沿AC方向移动到(图2)的位置时,其他条件不变,上述结论是否成立?请说明理由。
思路点播:图2中△ABF≌△CDE 和△DEG≌△BFG不变,可证得结论。
证明:如图1
∵AE=CF
∴AF=CE
又∵DE⊥AC,BF⊥AC ,AB=CD
∴△ABF≌△CDE
∴ BF=DE
又 ∵∠AFB=∠DEC=90°,∠EGD=∠FGB
∴△DEG≌△BFG
∴ EG=FG
即BD平分EF
当△DEC的边EC沿AC方向移动到(图2)的位置时,见结论仍然成立。
A
D
C
B
E
图3
A
D
C
B
E
图2
A
D
C
B
E
图1
F
A
D
C
B
E
图4
A
C
B
E
图5
A
D
C
B
E
图6
D
A
D
C
B
E
图9
A
D
C
B
E
图8
A
D
C
B
E
图7
M
E
D
C
B
A
P
图1
图2
M
E
D
C
B
A
F
P
M
E
D
C
B
A
P
图1
M
D
C
B
A
P
F
P
E
图3
M
E
D
C
B
A
P
F
图4
M
E
D
C
B
A
P
F
图4
B
A
F
E
D
C
图1
G
G
B
A
F
E
D
C
图2
- 4 -
几何中创新发展的思维策略,是新的(或条件,或图形的)变化将各种思维方法灵活应用,产生新思路的思维策略,是将创新精神,创新思维,创新技法综合使用,促进发展的思维策略。
几何中,在图形的多样变换下,解决问题。为培养学生的创新思维的发展提供了广阔的空间。下面,我们就几何中与图形变换有关的问题,从创新思维方法和技法两个方面,对与图形变换有关的问题作初步的探索。
1.如图1,△ABD与△CDE中均为等腰直角三角形,B,D,C三点在一直线上.
(1)试问BE与AC有何关系?并证明你的结论。
(2)当△CDE绕点D沿顺时针方向旋转如下图(图2)——(图9)时,BE与AC的关系分别怎样?
点拨(1)解决猜想并证明的问题,一般用综合法,从已知入手,将所给条件综合分析。本题中条件,△ABD与△CDE中均为等腰直角三角形,可得,AD=BD,∠ADB=∠EDC,ED=DC,所以△BDE≌△ADC,又因为几何中,判断两个量的关系,要考虑位置关系和数量关系,所以猜想:BE=AC,BE⊥AC。
答:(1)BE=AC,BE⊥AC
证明:延长BE交AC于F,
∵△ABD与△CDE中均为等腰直角三角形
在△BDE与中△ADC中:
∵AD=BD,∠ADB=∠EDC,ED=DC
∴△BDE≌△ADC
∴BE=AC,∠EAF=∠EBD,
∴∠EAF+∠AEF =∠EBD+∠BED=90°
∴∠AFE=90°即BE⊥AC
(2)(图2)——(图9)时,BE与AC的关系不变。
点拨:解这类题要特别注意图形的变化,从图形的变化中把握本质,找出某些固定不变的关系,即“变中寻不变”。猜想其规律,再运用几何知识加以证明。(其解题关键是“变中寻不变”。)本题图形位置虽然发生了几多变化,但本题本质上△BDE≌△ADC不变,(即变中的不变关系是△BDE≌△ADC,)其他位置时,同理(用“边角边”)可证得结论。图5,图9,可根据图直接求得。
2.已知:等边△ABC和点P,设点P到△ABC的三边AB,AC,BC的距离为h1,h2,h3,△ABC的高为h,“若点P在一边BC上,(如图1)此时h3=0,可得结论:h1+h2+h3=h”。请直接应用上述信息.解决下列问题:
当点P在△ABC内,(如图2),点P在△ABC外,(如图3),这两种情况时,上述结论是否成立?若成立,请给予证明;若不成立h1,h2,h3 与 h之间又有怎样的关系?请写出你的猜想,不需证明。
点拨:已知中“若点P在一边BC上,(如图1)此时h=0,可得结论:h1+h2+h3=h”的证明思路,连接AP,由S= S+S,即BC·AM=AB·PD+AC·PE,可得h1+h2+h3=h 。
(1)中,当点P在△ABC内时,点P的位置,及h1,h2,h3的大小发生变化,但是本题S的大小没有改变(即变中的不变关系是,S的大小不变),所以依然用S= S+S+S的关系即可证得结论。
(1) 当点P在△ABC内时,如图3,结论h1+h2+h3=h仍然成立。
证明:连接PA,PB,PC.
∵△ABC是等边三角形,∴AB=BC=AC.
∵AM⊥BC,∴S=BC·AM.
∵PD⊥AB,PE⊥AC,PF⊥BC.
∴S=AB·PD ,S=AC·PE ,S=BC·PF.
S= S+S+S.
∴BC·AM=AB·PD+AC·PE+BC·PF.
∴AM=PD+PE+PF,∴h1+h2+h3=h.
(2) 当P点在△ABC外部时,h1+h2+h3=h 不成立,此时h1+h2+h3=h.
点拨:(2)当P点在△ABC外部时,S= S+S - S,
即BC·AM=AB·PD+AC·PE - BC·PF,
所以h1+h2-h3=h.
同类练习:
如图1,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,求证:BD平分EF,
想一想 上题中,若将△DEC的边EC沿AC方向移动到(图2)的位置时,其他条件不变,上述结论是否成立?请说明理由。
思路点播:图2中△ABF≌△CDE 和△DEG≌△BFG不变,可证得结论。
证明:如图1
∵AE=CF
∴AF=CE
又∵DE⊥AC,BF⊥AC ,AB=CD
∴△ABF≌△CDE
∴ BF=DE
又 ∵∠AFB=∠DEC=90°,∠EGD=∠FGB
∴△DEG≌△BFG
∴ EG=FG
即BD平分EF
当△DEC的边EC沿AC方向移动到(图2)的位置时,见结论仍然成立。
A
D
C
B
E
图3
A
D
C
B
E
图2
A
D
C
B
E
图1
F
A
D
C
B
E
图4
A
C
B
E
图5
A
D
C
B
E
图6
D
A
D
C
B
E
图9
A
D
C
B
E
图8
A
D
C
B
E
图7
M
E
D
C
B
A
P
图1
图2
M
E
D
C
B
A
F
P
M
E
D
C
B
A
P
图1
M
D
C
B
A
P
F
P
E
图3
M
E
D
C
B
A
P
F
图4
M
E
D
C
B
A
P
F
图4
B
A
F
E
D
C
图1
G
G
B
A
F
E
D
C
图2
- 4 -
同课章节目录
