27.2.1 相似三角形的判定(第二课时)课件(共26张PPT)(wps版)-九年级数学下册同步备课系列(人教版)
文档属性
| 名称 | 27.2.1 相似三角形的判定(第二课时)课件(共26张PPT)(wps版)-九年级数学下册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 21:19:30 | ||
图片预览




文档简介
(共26张PPT)
第27章 相似
27.2.1 相似三角形的判定
第二单元
第二课时
复习巩固
探究新知
新知讲解
典例分析
归纳小结
针对训练
探究新知
新知讲解
探究新知
典例分析
针对训练
典例分析
针对训练
典例分析
归纳小结
布置作业
【提问1】简述相似三角形的概念?
【提问2】如何判断两个三角形是否相似呢?
【提问3】结合之前所学,判定两个三角形全等有几种方法?
如果三角分别相等、三边成比例的两个三角形叫做相似三角形.
1)定义法:对应角相等,对应边成比例的两个三角形相似。
2)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
一般三角形 直角三角形
判定 边角边(SAS)、角边角(ASA) 角角边(AAS)、边边边(SSS) 斜边和一条直角边对应相等(HL)
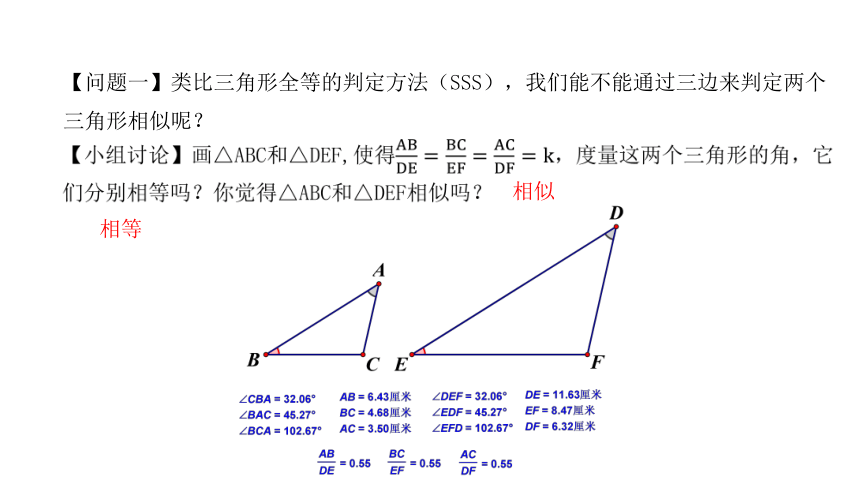
【问题一】类比三角形全等的判定方法(SSS),我们能不能通过三边来判定两个三角形相似呢?
相似
相等
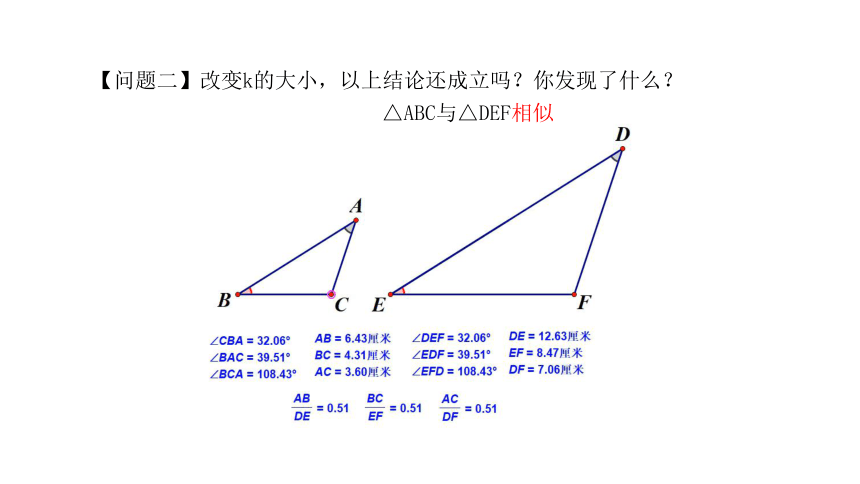
【问题二】改变k的大小,以上结论还成立吗?你发现了什么?
△ABC与△DEF相似
A
B
C
A'
B'
C'
D
E
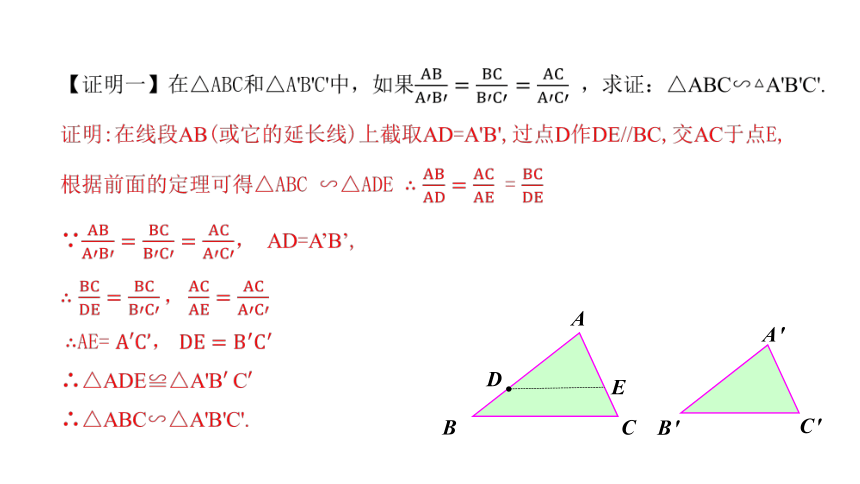
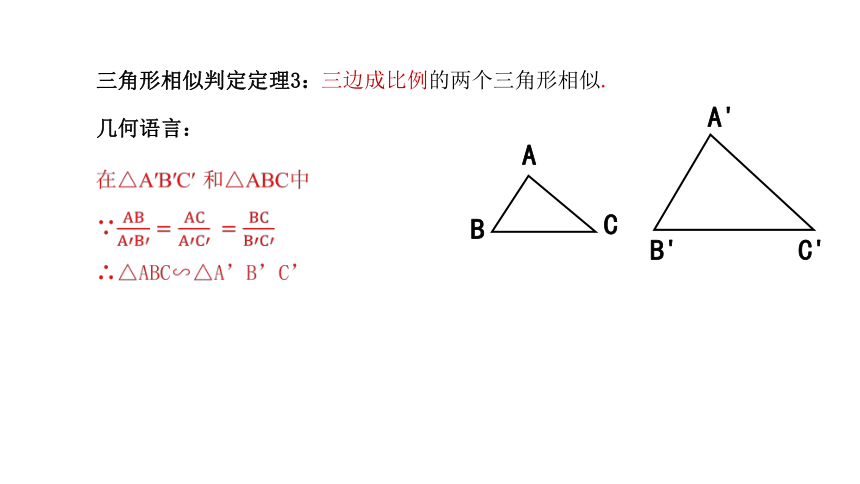
三角形相似判定定理3:
几何语言:
三边成比例的两个三角形相似.
A
C
B
C'
B'
A'
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
解:由图可知,
在 △ABC 中,AB > BC > CA
在 △ DEF中,DE > EF > FD
而
∴
∴ △ABC ∽ △DEF
【解题技巧】判定两个三角形相似时,如果题中给出了两个三角形的三边的长,首先算出三条对应边的比值,再看比值是否相等,如果相等,则两个三角形相似.
【易错点】计算时需注意:三角形中最长边与最长边对应,最短边与最短边对应.
2.下列四个三角形中,与图中的三角形相似的是( )
【问题三】类比三角形全等的判定方法(SAS),我们能不能通过三边来判定两个三角形相似呢?
相似
等于
【问题四】改变k的大小,以上结论还成立吗?你发现了什么?
A
B
C
A'
B'
C'
D
E
三角形相似判定定理4:
几何语言:
两边成比例且夹角相等的两个三角形相似.
A
C
B
C'
B'
A'
不一定相似
∠DAE=∠BAC
1. 如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
2.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
A
E
D
B
C
1.通过本节课的学习,你学会了哪些知识?
2. 简述判定两个三角形相似的方法?
P34:练习
第27章 相似
27.2.1 相似三角形的判定
第二单元
第二课时
复习巩固
探究新知
新知讲解
典例分析
归纳小结
针对训练
探究新知
新知讲解
探究新知
典例分析
针对训练
典例分析
针对训练
典例分析
归纳小结
布置作业
【提问1】简述相似三角形的概念?
【提问2】如何判断两个三角形是否相似呢?
【提问3】结合之前所学,判定两个三角形全等有几种方法?
如果三角分别相等、三边成比例的两个三角形叫做相似三角形.
1)定义法:对应角相等,对应边成比例的两个三角形相似。
2)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
一般三角形 直角三角形
判定 边角边(SAS)、角边角(ASA) 角角边(AAS)、边边边(SSS) 斜边和一条直角边对应相等(HL)
【问题一】类比三角形全等的判定方法(SSS),我们能不能通过三边来判定两个三角形相似呢?
相似
相等
【问题二】改变k的大小,以上结论还成立吗?你发现了什么?
△ABC与△DEF相似
A
B
C
A'
B'
C'
D
E
三角形相似判定定理3:
几何语言:
三边成比例的两个三角形相似.
A
C
B
C'
B'
A'
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
解:由图可知,
在 △ABC 中,AB > BC > CA
在 △ DEF中,DE > EF > FD
而
∴
∴ △ABC ∽ △DEF
【解题技巧】判定两个三角形相似时,如果题中给出了两个三角形的三边的长,首先算出三条对应边的比值,再看比值是否相等,如果相等,则两个三角形相似.
【易错点】计算时需注意:三角形中最长边与最长边对应,最短边与最短边对应.
2.下列四个三角形中,与图中的三角形相似的是( )
【问题三】类比三角形全等的判定方法(SAS),我们能不能通过三边来判定两个三角形相似呢?
相似
等于
【问题四】改变k的大小,以上结论还成立吗?你发现了什么?
A
B
C
A'
B'
C'
D
E
三角形相似判定定理4:
几何语言:
两边成比例且夹角相等的两个三角形相似.
A
C
B
C'
B'
A'
不一定相似
∠DAE=∠BAC
1. 如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
2.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
A
E
D
B
C
1.通过本节课的学习,你学会了哪些知识?
2. 简述判定两个三角形相似的方法?
P34:练习
