数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
2.5.1 直线与圆的位置关系
在我们的生活中到处都蕴含着数学知识,请同学们欣赏美丽的
海上日出
日出江花红胜火
春来江水绿如蓝
一:创设情境,引入课题
在日出的过程中,太阳和海天交线有哪些位置关系?
把太阳看作一个圆,海天交线看作一条直线,那么在日出的过程中,体现了直线和圆的哪些位置关系?
2.5.1 直线与圆的位置关系
教学目标
1.掌握直线与圆的位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的位置关系.(重点)
3.会用直线与圆的位置关系解决一些数学问题和实际问题(难点)
4.学科素养:直观想象 数学运算 逻辑推理
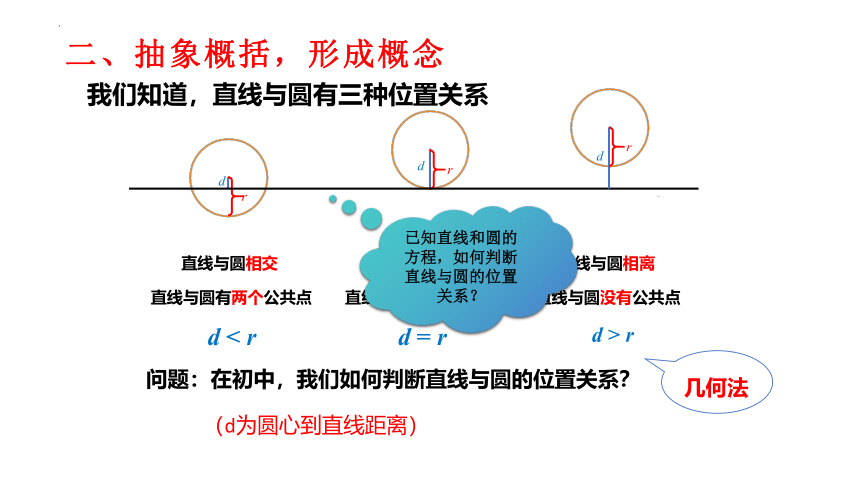
地平线
直线与圆相交
直线与圆相切
直线与圆相离
直线与圆有两个公共点
直线与圆有一个公共点
直线与圆没有公共点
r
d
r
d
r
d
d < r
d > r
d = r
已知直线和圆的方程,如何判断直线与圆的位置关系?
(d为圆心到直线距离)
几何法
我们知道,直线与圆有三种位置关系
二、抽象概括,形成概念
问题:在初中,我们如何判断直线与圆的位置关系?
思考1:如何用代数法研究两条直线位置关系?
l1: A1x+B1 y +C1=0, l2: A2x+B2 y +C2=0.
A1x+B1 y +C1=0,有一解 相交
A2x+B2 y +C2=0. 无解 平行
联立
代数方法
●直线l:Ax+By+C = 0
圆O:(x-a)2+(y-b)2 = r2(r>0)
将两个方程联立组成方程组
消元得到一元二次方程,求得判别式△
① △>0
方程有两不等实根
直线l与圆C相交;
② △=0
方程有两个相等实根
直线l与圆C相切;
③ △<0
方程无实数根
直线l与圆C相离.
思考2:类比用代数法研究两条直线位置关系的方法,
如何用代数方法,研究直线与圆的位置关系?
思路2:几何法
题型一 直线与圆的位置关系
y
O
C
B
A
r
d
思路1:代数法
若相交,直角三角形 ,勾股定理,求得弦长.
题型一 直线与圆的位置关系
例1:已知直线l : 3x+y-6=0和⊙C : x2+y2-2y-4=0,判断直线l与圆的位置关系,如果相交,求直线l被圆所截得的弦长.
x
y
O
C
B
A
r
d
图2.5-1
题型一 直线与圆的位置关系
例1:已知直线l : 3x+y-6=0和⊙C : x2+y2-2y-4=0,判断直线l与圆的位置关系,如果相交,求直线l被圆所截得的弦长.
1、判断直线与圆位置关系的方法
(1) 代数法:
消去y(或x), 得到关于x(或y)的一元二次方程.求得判别式△
(2) 几何法:
已知直线l: Ax+By+C=0, 圆C: (x-a)2 + (y-b)2=r2. 设圆心C到直线l的距离为d,
2、求弦长的方法
(1) 代数法
(2) 几何法:
变式训练1 :
判断直线2x-y+2=0与圆C:(x-1)2+(y-2)2=4的位置关系;如果相交,求直线被圆所截得的弦长.
思考:与初中的方法比较,你认为用方程判断直线与圆的位置关系有什么优点?例1中两种解法的差异是什么?
与初中的方法比较,用方程判断直线与圆的位置关系,不必作图,只需要通过代数运算即可完成,避免了画图时出现的误差,体现了解析几何的基本思想——几何问题代数化.
例1中的解法1,通过方程组的解进行判断和计算,是纯粹的代数方法.解法2,把几何条件代数化,即用距离公式直接计算出,是几何方法.
例2 过点P(2,1)作圆O:x2+y2=1 的切线 l,求切线 l 的方程.
题型二 直线与圆的相切问题
O
x
y
P
问题:同学们回顾一下初中学过哪些直线与圆相切的知识?(同位之间相互交流)
1.点在圆外可做两条切线,点在圆上可做1条切线,
点在圆内无切线
2.直线与圆只有一个交点(代数)
3.圆心到切线的距离等于半径(几何)
4.圆心与切点的连线与切线垂直
例2 求过点作圆: =1的切线,求切线的方程.
追问1:点与圆的位置关系是什么?
点在圆外
追问2:过圆外一点做圆的切线,能做几条切线?
两条
追问3:如何刻画直线与圆相切?
公共点的个数;圆心到直线的距离
追问4:直线方程选择什么形式?
点斜式;
注意:运用点斜式必须先判断斜率是否存在
例2 过点P(2,1)作圆O:x2+y2=1 的切线 l,求切线 l 的方程.
题型二 直线与圆的相切问题
思路2 几何法 1.设直线l的方程(考虑斜率是否存在)
2.
思路1代数法 1.设直线l的方程,考虑斜率是否存在
2.联立
3.解的个数
O
P
y
x
图2.5-2
题型二 直线与圆的相切问题
O
P
y
x
图2.5-2
题型二 直线与圆的相切问题
变式训练2:
同学们以小组为单位,讨论以上两题
求圆的切线方程的方法
四、课堂小结
1、知识方面
2、思想方法方面:数形结合的思想 转化与化归的思想
(1)判断直线与圆的位置关系(几何法、代数法)
(2)求直线与圆相交时的弦长(几何法、代数法)
(3)求过某一点的圆的切线方程(点在圆上、点在圆外)
(一)你的收获是什么
(二)你的疑惑是什么
当堂检测
B
B
五、作业布置
1.课本93页,2、3题
2.分层训练79页
2.5.1 直线与圆的位置关系
在我们的生活中到处都蕴含着数学知识,请同学们欣赏美丽的
海上日出
日出江花红胜火
春来江水绿如蓝
一:创设情境,引入课题
在日出的过程中,太阳和海天交线有哪些位置关系?
把太阳看作一个圆,海天交线看作一条直线,那么在日出的过程中,体现了直线和圆的哪些位置关系?
2.5.1 直线与圆的位置关系
教学目标
1.掌握直线与圆的位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的位置关系.(重点)
3.会用直线与圆的位置关系解决一些数学问题和实际问题(难点)
4.学科素养:直观想象 数学运算 逻辑推理
地平线
直线与圆相交
直线与圆相切
直线与圆相离
直线与圆有两个公共点
直线与圆有一个公共点
直线与圆没有公共点
r
d
r
d
r
d
d < r
d > r
d = r
已知直线和圆的方程,如何判断直线与圆的位置关系?
(d为圆心到直线距离)
几何法
我们知道,直线与圆有三种位置关系
二、抽象概括,形成概念
问题:在初中,我们如何判断直线与圆的位置关系?
思考1:如何用代数法研究两条直线位置关系?
l1: A1x+B1 y +C1=0, l2: A2x+B2 y +C2=0.
A1x+B1 y +C1=0,有一解 相交
A2x+B2 y +C2=0. 无解 平行
联立
代数方法
●直线l:Ax+By+C = 0
圆O:(x-a)2+(y-b)2 = r2(r>0)
将两个方程联立组成方程组
消元得到一元二次方程,求得判别式△
① △>0
方程有两不等实根
直线l与圆C相交;
② △=0
方程有两个相等实根
直线l与圆C相切;
③ △<0
方程无实数根
直线l与圆C相离.
思考2:类比用代数法研究两条直线位置关系的方法,
如何用代数方法,研究直线与圆的位置关系?
思路2:几何法
题型一 直线与圆的位置关系
y
O
C
B
A
r
d
思路1:代数法
若相交,直角三角形 ,勾股定理,求得弦长.
题型一 直线与圆的位置关系
例1:已知直线l : 3x+y-6=0和⊙C : x2+y2-2y-4=0,判断直线l与圆的位置关系,如果相交,求直线l被圆所截得的弦长.
x
y
O
C
B
A
r
d
图2.5-1
题型一 直线与圆的位置关系
例1:已知直线l : 3x+y-6=0和⊙C : x2+y2-2y-4=0,判断直线l与圆的位置关系,如果相交,求直线l被圆所截得的弦长.
1、判断直线与圆位置关系的方法
(1) 代数法:
消去y(或x), 得到关于x(或y)的一元二次方程.求得判别式△
(2) 几何法:
已知直线l: Ax+By+C=0, 圆C: (x-a)2 + (y-b)2=r2. 设圆心C到直线l的距离为d,
2、求弦长的方法
(1) 代数法
(2) 几何法:
变式训练1 :
判断直线2x-y+2=0与圆C:(x-1)2+(y-2)2=4的位置关系;如果相交,求直线被圆所截得的弦长.
思考:与初中的方法比较,你认为用方程判断直线与圆的位置关系有什么优点?例1中两种解法的差异是什么?
与初中的方法比较,用方程判断直线与圆的位置关系,不必作图,只需要通过代数运算即可完成,避免了画图时出现的误差,体现了解析几何的基本思想——几何问题代数化.
例1中的解法1,通过方程组的解进行判断和计算,是纯粹的代数方法.解法2,把几何条件代数化,即用距离公式直接计算出,是几何方法.
例2 过点P(2,1)作圆O:x2+y2=1 的切线 l,求切线 l 的方程.
题型二 直线与圆的相切问题
O
x
y
P
问题:同学们回顾一下初中学过哪些直线与圆相切的知识?(同位之间相互交流)
1.点在圆外可做两条切线,点在圆上可做1条切线,
点在圆内无切线
2.直线与圆只有一个交点(代数)
3.圆心到切线的距离等于半径(几何)
4.圆心与切点的连线与切线垂直
例2 求过点作圆: =1的切线,求切线的方程.
追问1:点与圆的位置关系是什么?
点在圆外
追问2:过圆外一点做圆的切线,能做几条切线?
两条
追问3:如何刻画直线与圆相切?
公共点的个数;圆心到直线的距离
追问4:直线方程选择什么形式?
点斜式;
注意:运用点斜式必须先判断斜率是否存在
例2 过点P(2,1)作圆O:x2+y2=1 的切线 l,求切线 l 的方程.
题型二 直线与圆的相切问题
思路2 几何法 1.设直线l的方程(考虑斜率是否存在)
2.
思路1代数法 1.设直线l的方程,考虑斜率是否存在
2.联立
3.解的个数
O
P
y
x
图2.5-2
题型二 直线与圆的相切问题
O
P
y
x
图2.5-2
题型二 直线与圆的相切问题
变式训练2:
同学们以小组为单位,讨论以上两题
求圆的切线方程的方法
四、课堂小结
1、知识方面
2、思想方法方面:数形结合的思想 转化与化归的思想
(1)判断直线与圆的位置关系(几何法、代数法)
(2)求直线与圆相交时的弦长(几何法、代数法)
(3)求过某一点的圆的切线方程(点在圆上、点在圆外)
(一)你的收获是什么
(二)你的疑惑是什么
当堂检测
B
B
五、作业布置
1.课本93页,2、3题
2.分层训练79页
