4.2力的分解课件 (共39张PPT) 高一上学期物理鲁科版(2019)必修第一册
文档属性
| 名称 | 4.2力的分解课件 (共39张PPT) 高一上学期物理鲁科版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-02 07:45:57 | ||
图片预览









文档简介
(共39张PPT)
第四章 力与平衡
第二节 力的分解
教学目标
01
知道什么是力的分解,知道力的分解是力的合成的逆运算
02
了解力的分解的一般方法,会用正交分解解决一般问题
03
体会力的分解在实际生活生产中的作用及意义
01
力的分解
力的分解
用以下几种方法挂物体,哪种情况线易断?为什么?
甲图线容易断。合力一定,两分力大小相等的情况下,分力间夹角越大,分力越大。
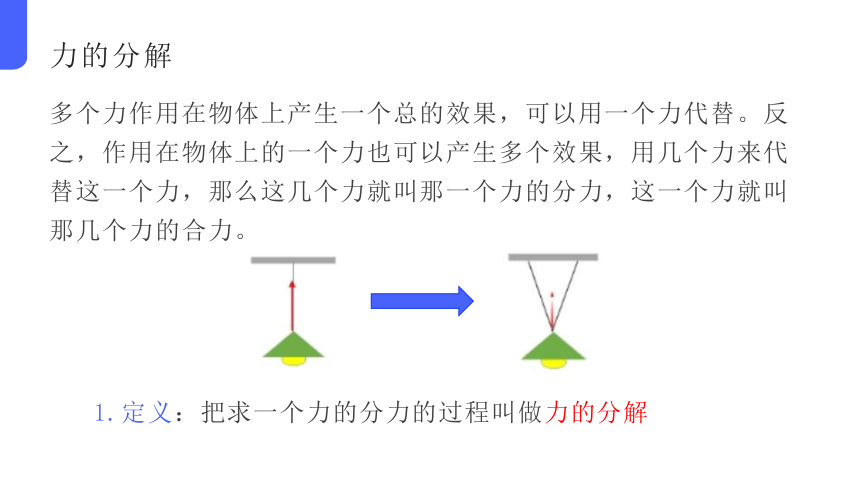
多个力作用在物体上产生一个总的效果,可以用一个力代替。反之,作用在物体上的一个力也可以产生多个效果,用几个力来代替这一个力,那么这几个力就叫那一个力的分力,这一个力就叫那几个力的合力。
力的分解
1.定义:把求一个力的分力的过程叫做力的分解
2.依据:力的分解是力的合成的逆运算,也遵循平行四边形定则。
力的分解
不同的是:力的合成,是已知邻边求对角线;而力的分解,是已知对角线求邻边
F
力的分解
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边就表示力F的两个分力。
如果没有其他限制,对于同一条对角线,可以作出无数个不同的平行四边形。
一个力可以分解成无数对力
一个已知力究竟应该怎样分解,要根据具体问题来确定。
02
按力的效果分解
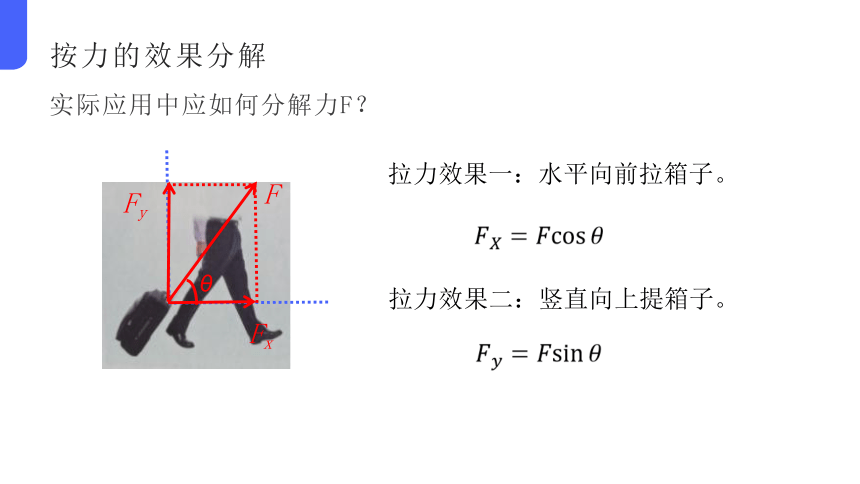
实际应用中应如何分解力F?
按力的效果分解
F
拉力效果一:水平向前拉箱子。
拉力效果二:竖直向上提箱子。
Fx
Fy
θ
按力的效果分解
G
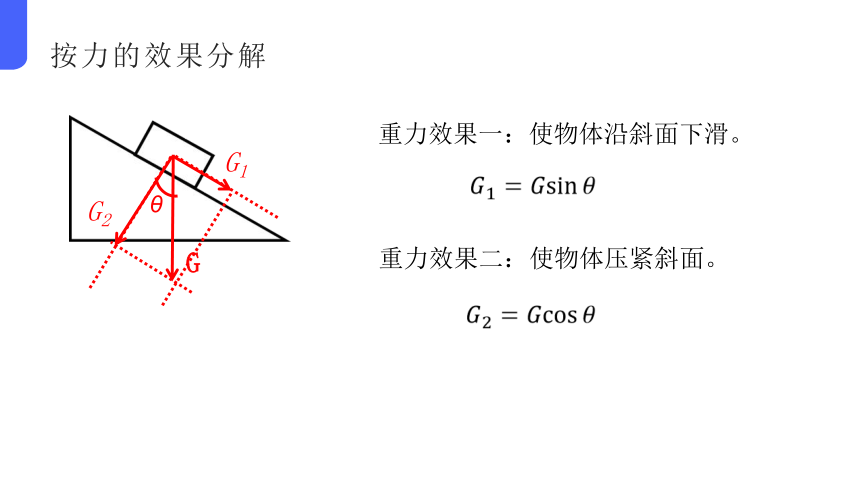
重力效果一:使物体沿斜面下滑。
重力效果二:使物体压紧斜面。
G1
G2
θ
按力的效果分解
1.力的分解的实质
将一个已知力F进行分解,其实质是寻找等效分力的过程。一个力可以分解为两个力,也可以分解为更多力,但这几个分力不是物体实际受到的力,是“等效替代法”的应用。
按力的效果分解
2.按实际效果分解的几个实例
实例 分析
(1)拉力F的效果
①使物体沿水平地面前进(或有前进趋势);
②向上提物体。
(2)两个分力:水平向前的力F1和竖直向上的力F2。
F1=Fcos α,F2=Fsin α
按力的效果分解
实例 分析
(1)重力的两个效果
①使物体沿斜面下滑(或有下滑趋势);
②使物体垂直压紧斜面。
(2)分力大小:
F1=mgsin α, F2=mgcos α
按力的效果分解
实例 分析
按力的效果分解
实例 分析
按力的效果分解
实例 分析
按力的效果分解
实例 分析
[例题1] 如图所示,AB、AC两光滑斜面互相垂直,AC与水平面成30°角。若把球O的重力(大小为G)按照其作用效果分解,则两个分力的大小为 ( )
A.G,G B.G,G
C.G,G D.G,G
按力的效果分解
按力的效果分解
[解析] 对球所受重力进行分解,如图所示,由几何关系得F1=Gsin 60°=G,F2=Gsin 30°=G,选项A正确。
按力的效果分解
按效果分解的基本思路
03
力的正交分解
力的正交分解
1.定义:把一个已知力沿着两个互相垂直的方向进行分解
2.力的正交分解目的
正交分解,“分”是为了更好地“合”。
3.正交分解步骤:
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力落在坐标轴上。
力的正交分解
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示。
(3)分别求出x轴、y轴上各力的分力的合力,即Fx合=F1x-F2x-F3x,Fy合=F1y+F2y-F3y。
(4)求共点力的合力:合力大小F合= ,合力的方向与x轴的夹角为α,则 。
力的正交分解
[例题2] 在同一平面内的四个共点力F1、F2、F3、F4的大小依次为19 N、40 N、30 N和15 N,方向如图所示,求它们的合力。
x
y
F2y
F3y
F2x
F3x
力的正交分解
[解析]如图甲所示,建立直角坐标系,把各个力分解到两个坐标轴上,并求出x轴和y轴上的合力Fx和Fy,有Fx=F1+F2cos 37°-F3cos 37°=27 NFy=F2sin 37°+F3sin 37°-F4=27 N因此,如图乙所示,合力F= ≈38.2 N
=1即合力的大小约为38.2 N,方向与F1夹角为45°斜向上。
力的正交分解
建立坐标系的原则原则上坐标系的建立是任意的,为使问题简化,一般考虑以下两个问题:(1)使尽量多的力处在坐标轴上。(2)尽量使待求力处在坐标轴上。
04
力的分解讨论
力的分解讨论
1.不受限制条件的分解
将某个力进行分解,如果没有条件约束,从理论上讲有无数组解,因为同一条对角线可以构成的平行四边形有无穷多个(如图所示),这样分解是没有实际意义的。实际分解时,一个力按力的作用效果可分解为两个确定的分力。
力的分解讨论
2.有限制条件的力的分解
(1)已知合力和两个分力的方向时,有唯一解(如图)。
力的分解讨论
2.有限制条件的力的分解
(2)已知合力和一个分力的大小和方向时,有唯一解(如图)。
力的分解讨论
(3)已知合力以及一个分力F2的大小和另一个分力F1的方向时,有下面几种可能:
①当F sin θ②当F2=F sin θ时,F1有唯一解[如图(2)];
力的分解讨论
2.有限制条件的力的分解
③当F2④当F2>F时,F1有唯一解[如图(4)]。
力的分解讨论
[例题3]将一个大小为10 N且有确定方向的力F分解成两个力,已知一个分力有确定的方向,与F夹角为30°,另一个分力的大小为6 N,则在分解时 ( )
A.有无数组解 B.有两组解 C.有唯一解 D.无解
解析 设方向已知的分力为F1,如图所示,则F2的最小值F2min=F sin 30°=5 N。因5 N05
力的分解应用
力的分解应用
高大的桥为什么要造很长的引桥?
G
G1
G2
θ
减小斜面的倾角,从而减小重力沿斜面向下的分力。这样上桥时省力,下桥时安全。
力的分解应用
盘山公路
斧刃越薄越好
力的分解应用
两只手拉橡皮筋,使钩码静止。
合力一定时,两等大分力随它们之间夹角的增大而增大。
力的分解应用
为什么斧刃越薄越好?
θ角越小(即斧刃越薄),F1 就越大
THANK YOU
第四章 力与平衡
第二节 力的分解
教学目标
01
知道什么是力的分解,知道力的分解是力的合成的逆运算
02
了解力的分解的一般方法,会用正交分解解决一般问题
03
体会力的分解在实际生活生产中的作用及意义
01
力的分解
力的分解
用以下几种方法挂物体,哪种情况线易断?为什么?
甲图线容易断。合力一定,两分力大小相等的情况下,分力间夹角越大,分力越大。
多个力作用在物体上产生一个总的效果,可以用一个力代替。反之,作用在物体上的一个力也可以产生多个效果,用几个力来代替这一个力,那么这几个力就叫那一个力的分力,这一个力就叫那几个力的合力。
力的分解
1.定义:把求一个力的分力的过程叫做力的分解
2.依据:力的分解是力的合成的逆运算,也遵循平行四边形定则。
力的分解
不同的是:力的合成,是已知邻边求对角线;而力的分解,是已知对角线求邻边
F
力的分解
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边就表示力F的两个分力。
如果没有其他限制,对于同一条对角线,可以作出无数个不同的平行四边形。
一个力可以分解成无数对力
一个已知力究竟应该怎样分解,要根据具体问题来确定。
02
按力的效果分解
实际应用中应如何分解力F?
按力的效果分解
F
拉力效果一:水平向前拉箱子。
拉力效果二:竖直向上提箱子。
Fx
Fy
θ
按力的效果分解
G
重力效果一:使物体沿斜面下滑。
重力效果二:使物体压紧斜面。
G1
G2
θ
按力的效果分解
1.力的分解的实质
将一个已知力F进行分解,其实质是寻找等效分力的过程。一个力可以分解为两个力,也可以分解为更多力,但这几个分力不是物体实际受到的力,是“等效替代法”的应用。
按力的效果分解
2.按实际效果分解的几个实例
实例 分析
(1)拉力F的效果
①使物体沿水平地面前进(或有前进趋势);
②向上提物体。
(2)两个分力:水平向前的力F1和竖直向上的力F2。
F1=Fcos α,F2=Fsin α
按力的效果分解
实例 分析
(1)重力的两个效果
①使物体沿斜面下滑(或有下滑趋势);
②使物体垂直压紧斜面。
(2)分力大小:
F1=mgsin α, F2=mgcos α
按力的效果分解
实例 分析
按力的效果分解
实例 分析
按力的效果分解
实例 分析
按力的效果分解
实例 分析
[例题1] 如图所示,AB、AC两光滑斜面互相垂直,AC与水平面成30°角。若把球O的重力(大小为G)按照其作用效果分解,则两个分力的大小为 ( )
A.G,G B.G,G
C.G,G D.G,G
按力的效果分解
按力的效果分解
[解析] 对球所受重力进行分解,如图所示,由几何关系得F1=Gsin 60°=G,F2=Gsin 30°=G,选项A正确。
按力的效果分解
按效果分解的基本思路
03
力的正交分解
力的正交分解
1.定义:把一个已知力沿着两个互相垂直的方向进行分解
2.力的正交分解目的
正交分解,“分”是为了更好地“合”。
3.正交分解步骤:
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力落在坐标轴上。
力的正交分解
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示。
(3)分别求出x轴、y轴上各力的分力的合力,即Fx合=F1x-F2x-F3x,Fy合=F1y+F2y-F3y。
(4)求共点力的合力:合力大小F合= ,合力的方向与x轴的夹角为α,则 。
力的正交分解
[例题2] 在同一平面内的四个共点力F1、F2、F3、F4的大小依次为19 N、40 N、30 N和15 N,方向如图所示,求它们的合力。
x
y
F2y
F3y
F2x
F3x
力的正交分解
[解析]如图甲所示,建立直角坐标系,把各个力分解到两个坐标轴上,并求出x轴和y轴上的合力Fx和Fy,有Fx=F1+F2cos 37°-F3cos 37°=27 NFy=F2sin 37°+F3sin 37°-F4=27 N因此,如图乙所示,合力F= ≈38.2 N
=1即合力的大小约为38.2 N,方向与F1夹角为45°斜向上。
力的正交分解
建立坐标系的原则原则上坐标系的建立是任意的,为使问题简化,一般考虑以下两个问题:(1)使尽量多的力处在坐标轴上。(2)尽量使待求力处在坐标轴上。
04
力的分解讨论
力的分解讨论
1.不受限制条件的分解
将某个力进行分解,如果没有条件约束,从理论上讲有无数组解,因为同一条对角线可以构成的平行四边形有无穷多个(如图所示),这样分解是没有实际意义的。实际分解时,一个力按力的作用效果可分解为两个确定的分力。
力的分解讨论
2.有限制条件的力的分解
(1)已知合力和两个分力的方向时,有唯一解(如图)。
力的分解讨论
2.有限制条件的力的分解
(2)已知合力和一个分力的大小和方向时,有唯一解(如图)。
力的分解讨论
(3)已知合力以及一个分力F2的大小和另一个分力F1的方向时,有下面几种可能:
①当F sin θ
力的分解讨论
2.有限制条件的力的分解
③当F2
力的分解讨论
[例题3]将一个大小为10 N且有确定方向的力F分解成两个力,已知一个分力有确定的方向,与F夹角为30°,另一个分力的大小为6 N,则在分解时 ( )
A.有无数组解 B.有两组解 C.有唯一解 D.无解
解析 设方向已知的分力为F1,如图所示,则F2的最小值F2min=F sin 30°=5 N。因5 N
力的分解应用
力的分解应用
高大的桥为什么要造很长的引桥?
G
G1
G2
θ
减小斜面的倾角,从而减小重力沿斜面向下的分力。这样上桥时省力,下桥时安全。
力的分解应用
盘山公路
斧刃越薄越好
力的分解应用
两只手拉橡皮筋,使钩码静止。
合力一定时,两等大分力随它们之间夹角的增大而增大。
力的分解应用
为什么斧刃越薄越好?
θ角越小(即斧刃越薄),F1 就越大
THANK YOU
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
