中考阅读理解题的几种类型
图片预览

文档简介
中考阅读理解题的几种类型
阅读理解型问题在近年的全国各地的中考试题中频频出现,阅读理解型问题除了考查学生的分析、综合、抽象、概括等演绎推理能力,即逻辑推理能力外,还经常考查学生的观察、猜想、不完全归纳、类比、联想等合情推理能力,考查学生的直觉思维.因此,这类问题需要学生通过对阅读材料的阅读理解,然后进行合情推理,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理.
定义新运算型
定义新运算型阅读理解题,通常是先定义一个运算法则,你只要根据所提供的运算法则,代入相应的数据求出结果即可。
例1:在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式,因式分解的结果是,若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式,取x=10,y=10时,用上述方法产生的密码是: ▲ (写出一个即可).
分析:阅读本题我们可以发现,“因式分解”法产生密码就是将用来产生密码的多项式先因式分解,然后将未知数的值代入即可。由于因式分解后各因式的书写顺序并不唯一,因此所得到的密码也不唯一。因式分解的结果可以是、、等等,所以将x=10, y=10代入的结果也就多样了,1090110、1011090、1109010等等,共6种。
例2:现规定一种新的运算“”:,如,则=( )
A. B. 8 C. D.
分析:根据题意可以发现表示的3次方。因此答案选A。
1、 探索规律型
探索数列规律型的阅读理解题,通常是给出或让你算出前几项数列,然后要你推出一般的规律性。探索规律的时候我们可以根据数列变化的情况来猜想,也可以根据图形的变化来作相应的猜想,得出一般的规律性后,在代入前几项数据进行检验。探索图形变化时不变的规律型阅读理解题,通常题目会提供一道题目的解题过程,然后变化图形让我们探究有什么成立的结论,我们可以由已知条件中所提供的解题方法作类似联想,找出解题的途径。
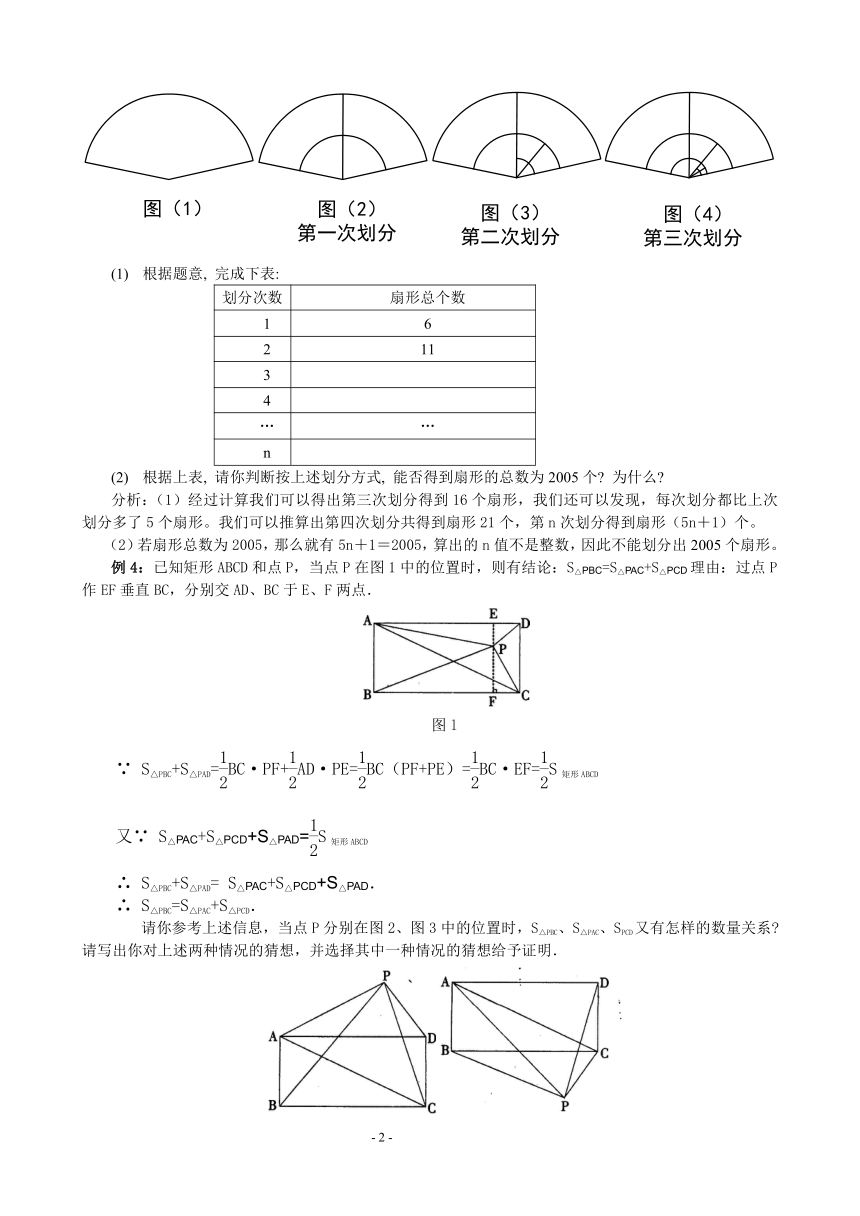
例3:下图中, 图(1)是一个扇形AOB,将其作如下划分:
第一次划分: 如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线, 得到扇形的总数为6个, 分别为: 扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;
第二次划分: 如图(3)所示, 在扇形C1OB1中, 按上述划分方式继续划分, 可以得到扇形的总数为11个;
第三次划分: 如图(4)所示;
……
依次划分下去.
(1) 根据题意, 完成下表:
划分次数 扇形总个数
1 6
2 11
3
4
… …
n
(2) 根据上表, 请你判断按上述划分方式, 能否得到扇形的总数为2005个 为什么
分析:(1)经过计算我们可以得出第三次划分得到16个扇形,我们还可以发现,每次划分都比上次划分多了5个扇形。我们可以推算出第四次划分共得到扇形21个,第n次划分得到扇形(5n+1)个。
(2)若扇形总数为2005,那么就有5n+1=2005,算出的n值不是整数,因此不能划分出2005个扇形。
例4:已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
图l
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴ S△PBC+S△PAD= S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系 请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
图2 图3
分析:这道中考题属于探究变化图形中的不变的规律型阅读理解题。通过题目对当点P在矩形内部的解析,我们不难发现解决问题的思路是证明等式的两边同时加上△PAD的面积后都等于矩形面积的一半,进而推出结论成立。因此解决当点P在矩形外部的时候,我们仍从考虑S△PAD与S△PBC、S△PAC、SPCD的关系方面着手。解:猜想结果:图2结论S△PBC=S△PAC+S△PCD; 图3结论S△PBC=S△PAC-S△PCD
证明:如图2,过点P作EF垂直AD,分别交AD、BC于E、F两点.
∵ S△PBC=BC·PF=BC·PE+BC·EF
=AD·PE+BC·EF=S△PAD+S矩形ABCD
S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD
∴ S△PBC=S△PAC+S△PCD
如图3:∵S△PAD-S△PBC=S矩形ABCD
又∵S△PAD+S△PCD-S△PAC=S矩形ABCD
∴S△PBC=S△PAC-S△PCD
三.应用新知识型
应用新知识型阅读理解题通常先在题目中介绍一种新知识,然后要你根据所学的新知识解题。解题时必须深刻理解题目所提供的新知识所表达的含义,并能熟练运用新知识解决问题。
例5:某校数学课外活动探究小组,在老师的指导下进一步研究了完全平方公式结合实数的性质发现以下规律:对于任意正数a、b,都有a+b≥成立。
某同学在做一个面积为3600cm2,对角线互相垂直的四边形风筝时,运用上述规律,求得用来做对角线的木条至少需要准备xcm,则x的值是( )
A. B. C.120 D.60
分析:设两条对角线的长分别为x、y,由于四边形对角线互相垂直,因此该四边形的面积可以表示为,从而得到.根据公式“a+b≥”可知x+y≥.所以本题答案为B。
例6:火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~389次为普快列车,401~598次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京.根据以上规定,杭州开往北京的某一直快列车的车次号可能是( )
(A)20 (B)119 (C)220 (D)319
分析:阅读题目可以得知直快列车的车次号应该在101~198,在上面四个选项中,只有B答案符合要求。
四:操作型阅读理解题
操作型阅读理解题通常先提供图形变化的方法步骤。解题的时候,你只要根据题目所提供的操作步骤一步步解题即可。
例7:如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到△的位置(在上),最后沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)。
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
分析:由于∠ACB=90°,∠CAB=30°,BC=1米。易得AB=2米,AC=米,当按顺时针方向绕点B翻转到△的位置(在上)时,点A的运动轨迹是以B为圆心、2米为半径、1200的扇形圆弧。当沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)时,其△上每个点平移的距离都是AC的长米。所以该路径的长度的约为5.9米。
- 3 -
阅读理解型问题在近年的全国各地的中考试题中频频出现,阅读理解型问题除了考查学生的分析、综合、抽象、概括等演绎推理能力,即逻辑推理能力外,还经常考查学生的观察、猜想、不完全归纳、类比、联想等合情推理能力,考查学生的直觉思维.因此,这类问题需要学生通过对阅读材料的阅读理解,然后进行合情推理,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理.
定义新运算型
定义新运算型阅读理解题,通常是先定义一个运算法则,你只要根据所提供的运算法则,代入相应的数据求出结果即可。
例1:在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式,因式分解的结果是,若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式,取x=10,y=10时,用上述方法产生的密码是: ▲ (写出一个即可).
分析:阅读本题我们可以发现,“因式分解”法产生密码就是将用来产生密码的多项式先因式分解,然后将未知数的值代入即可。由于因式分解后各因式的书写顺序并不唯一,因此所得到的密码也不唯一。因式分解的结果可以是、、等等,所以将x=10, y=10代入的结果也就多样了,1090110、1011090、1109010等等,共6种。
例2:现规定一种新的运算“”:,如,则=( )
A. B. 8 C. D.
分析:根据题意可以发现表示的3次方。因此答案选A。
1、 探索规律型
探索数列规律型的阅读理解题,通常是给出或让你算出前几项数列,然后要你推出一般的规律性。探索规律的时候我们可以根据数列变化的情况来猜想,也可以根据图形的变化来作相应的猜想,得出一般的规律性后,在代入前几项数据进行检验。探索图形变化时不变的规律型阅读理解题,通常题目会提供一道题目的解题过程,然后变化图形让我们探究有什么成立的结论,我们可以由已知条件中所提供的解题方法作类似联想,找出解题的途径。
例3:下图中, 图(1)是一个扇形AOB,将其作如下划分:
第一次划分: 如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线, 得到扇形的总数为6个, 分别为: 扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;
第二次划分: 如图(3)所示, 在扇形C1OB1中, 按上述划分方式继续划分, 可以得到扇形的总数为11个;
第三次划分: 如图(4)所示;
……
依次划分下去.
(1) 根据题意, 完成下表:
划分次数 扇形总个数
1 6
2 11
3
4
… …
n
(2) 根据上表, 请你判断按上述划分方式, 能否得到扇形的总数为2005个 为什么
分析:(1)经过计算我们可以得出第三次划分得到16个扇形,我们还可以发现,每次划分都比上次划分多了5个扇形。我们可以推算出第四次划分共得到扇形21个,第n次划分得到扇形(5n+1)个。
(2)若扇形总数为2005,那么就有5n+1=2005,算出的n值不是整数,因此不能划分出2005个扇形。
例4:已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
图l
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴ S△PBC+S△PAD= S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系 请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
图2 图3
分析:这道中考题属于探究变化图形中的不变的规律型阅读理解题。通过题目对当点P在矩形内部的解析,我们不难发现解决问题的思路是证明等式的两边同时加上△PAD的面积后都等于矩形面积的一半,进而推出结论成立。因此解决当点P在矩形外部的时候,我们仍从考虑S△PAD与S△PBC、S△PAC、SPCD的关系方面着手。解:猜想结果:图2结论S△PBC=S△PAC+S△PCD; 图3结论S△PBC=S△PAC-S△PCD
证明:如图2,过点P作EF垂直AD,分别交AD、BC于E、F两点.
∵ S△PBC=BC·PF=BC·PE+BC·EF
=AD·PE+BC·EF=S△PAD+S矩形ABCD
S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD
∴ S△PBC=S△PAC+S△PCD
如图3:∵S△PAD-S△PBC=S矩形ABCD
又∵S△PAD+S△PCD-S△PAC=S矩形ABCD
∴S△PBC=S△PAC-S△PCD
三.应用新知识型
应用新知识型阅读理解题通常先在题目中介绍一种新知识,然后要你根据所学的新知识解题。解题时必须深刻理解题目所提供的新知识所表达的含义,并能熟练运用新知识解决问题。
例5:某校数学课外活动探究小组,在老师的指导下进一步研究了完全平方公式结合实数的性质发现以下规律:对于任意正数a、b,都有a+b≥成立。
某同学在做一个面积为3600cm2,对角线互相垂直的四边形风筝时,运用上述规律,求得用来做对角线的木条至少需要准备xcm,则x的值是( )
A. B. C.120 D.60
分析:设两条对角线的长分别为x、y,由于四边形对角线互相垂直,因此该四边形的面积可以表示为,从而得到.根据公式“a+b≥”可知x+y≥.所以本题答案为B。
例6:火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~389次为普快列车,401~598次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京.根据以上规定,杭州开往北京的某一直快列车的车次号可能是( )
(A)20 (B)119 (C)220 (D)319
分析:阅读题目可以得知直快列车的车次号应该在101~198,在上面四个选项中,只有B答案符合要求。
四:操作型阅读理解题
操作型阅读理解题通常先提供图形变化的方法步骤。解题的时候,你只要根据题目所提供的操作步骤一步步解题即可。
例7:如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到△的位置(在上),最后沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)。
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
分析:由于∠ACB=90°,∠CAB=30°,BC=1米。易得AB=2米,AC=米,当按顺时针方向绕点B翻转到△的位置(在上)时,点A的运动轨迹是以B为圆心、2米为半径、1200的扇形圆弧。当沿的方向平移到△的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)时,其△上每个点平移的距离都是AC的长米。所以该路径的长度的约为5.9米。
- 3 -
同课章节目录
