七年级数学上册试题 5.2图形的运动-苏科版(含答案)
文档属性
| 名称 | 七年级数学上册试题 5.2图形的运动-苏科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 13:23:58 | ||
图片预览



文档简介
5.2图形的运动
一.选择题
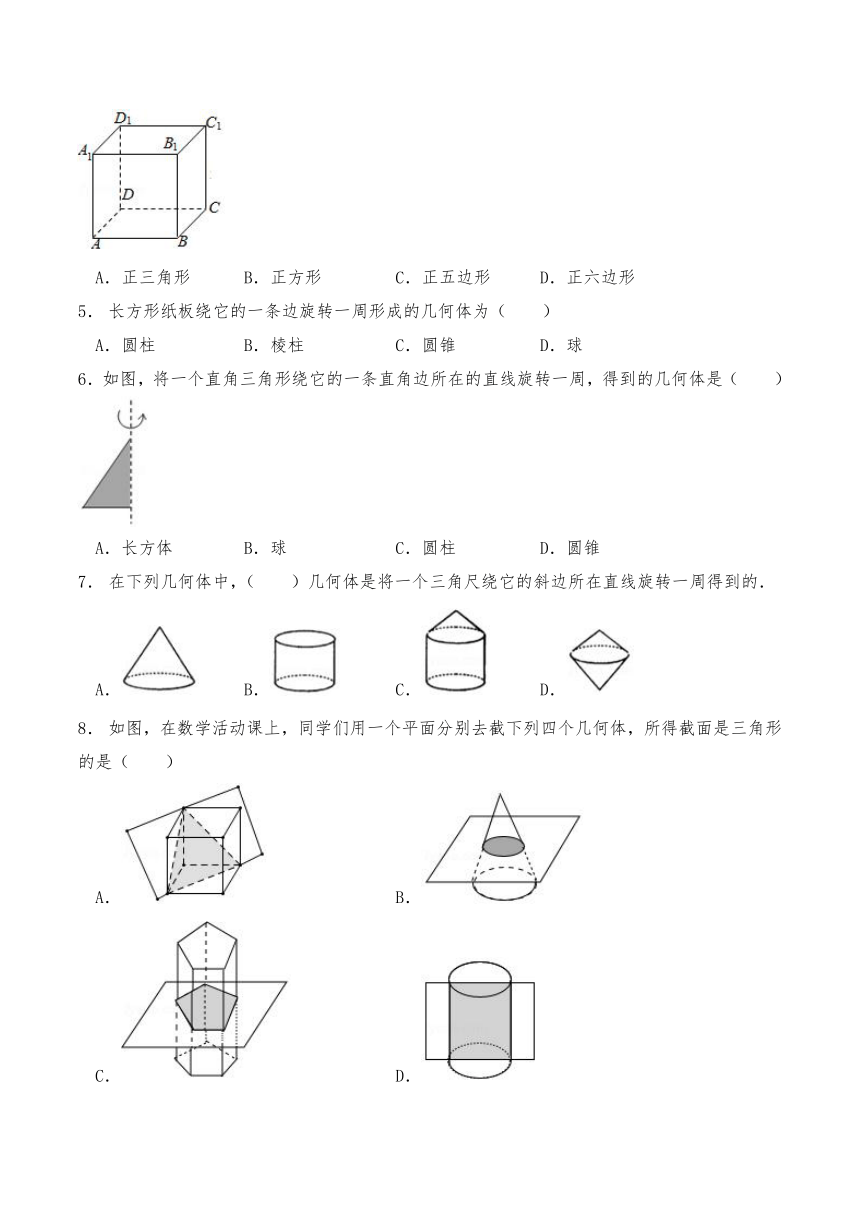
1. “节日的焰火”可以说是( )
A.面与面交于线 B.点动成线
C.面动成体 D.线动成面
2. 将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A. B. C. D.
3. 如图,在下列图形中,绕铅垂线旋转一周可得到如图所示几何体的是( )
A. B. C. D.
4. 用一个平面去截正方体ABCD﹣A1B1C1D1(如图),所截得的截面不可能的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
5. 长方形纸板绕它的一条边旋转一周形成的几何体为( )
A.圆柱 B.棱柱 C.圆锥 D.球
6.如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是( )
A.长方体 B.球 C.圆柱 D.圆锥
7. 在下列几何体中,( )几何体是将一个三角尺绕它的斜边所在直线旋转一周得到的.
A. B. C. D.
8. 如图,在数学活动课上,同学们用一个平面分别去截下列四个几何体,所得截面是三角形的是( )
A. B.
C. D.
9. 如图,小明将装有一半水的密闭圆柱形玻璃杯水平放置,此时水面的形状为( )
A.圆 B.长方形 C.平行四边形 D.椭圆
10.一块长方体豆腐切三刀,最多能切成的块数(形状,大小不限)是( )
A.10 B.8 C.7 D.6
11.“笔尖在纸上快速滑动写出数字6”,运用数学知识解释这一现象( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交得线
12.下列语句中,不正确的是( )
A.图形平移是由移动的方向和距离所决定
B.图形旋转是由旋转中心和旋转角度所决定
C.中心对称图形是指一个图形绕其中的某一点旋转180°后能与其自身重合的图形
D.旋转后能重合的图形也是中心对称图形
13.如图是一个长方体截去两个角后的立体图形,如果照这样截去长方体的八个角,那么新的几何体的棱有( )
A.26条 B.30条 C.36条 D.42条
14.如图,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
二.填空题
15.一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的的体积是 立方厘米.(结果保留π)
16.将一根长4米的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60平方分米,这根木料的体积是 立方分米.
17.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说 .
18.用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;③可能是长方形;④可能是梯形.
其中正确结论的是 (填序号).
19.如图,一个5×5×5的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为 .
20.如图是一个三棱柱,用平面从中截去一个三棱柱后,剩下的几何体是 (写出所有可能的结果).
21.如图所示的几何体的截面形状分别是: .
22.已知一个直角三角形的两直角边分别是6cm,8cm.将这个直角三角形绕它的一直角边所在直线旋转一周,可以得到一个圆锥,则这个圆锥的体积是 cm3.(结果用π表示)
23.“齐天大圣”孙悟空有一个宝贝﹣﹣金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明 .
24.用一个平面去截长方体,截面 是正五边形(填“可能”或“不可能”).
三.解答题
25.一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
26.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为8cm、宽为4cm的长方形,统它的一条边所在的直线旋转一周,求得到的圆柱体的体积是多少?
27.第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.
图1旋转形成 ,图2旋转形成 ,图3旋转形成 ,
图4旋转形成 ,图5旋转形成 ,图6旋转形成 .
28.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形.如图,大正三棱柱的底面周长为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请直接写出四边形DECB的周长.
29.如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.问:
(1)小立方体中三面红的有几块?两面红的呢?一面红的呢?没有红色的面呢?
(2)如果每面切三刀,情况又怎样呢?
(3)每面切n刀呢?
30.在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体,V圆锥h)
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
答案
一.选择题
B.C.A.C.A.D.D.A.B.B.A.D.C.D.
二.填空题
15.12π或16π.
16.1200.
17.线动成面
18.①③④.
19.49.
20.三棱柱或四棱柱
21.长方形、圆、三角形
22.128π或96π.
23.线动成面
24.可能.
三.解答题
25.18.84÷3=6.28(分米),
6.28÷3.14÷2=1(分米),
3.14×12×3=9.42(立方分米);
3.14×12×2+18.84=25.12(平方分米).
答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
26.①绕长所在的直线旋转一周得到圆柱体积为:π×42×8=128π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×82×4=256π(cm3).
答:得到的圆柱体的体积是分别是128π(cm3)和256π(cm3)
27.图1旋转形成d,图2旋转形成a,图3旋转形成c,
图4旋转形成f,图5旋转形成b,图6旋转形成e.
28.(1)由题可得,截面的形状为长方形;
(2)∵△ADE是周长为3的等边三角形,
∴DE=AD=1,
又∵△ABC是周长为10的等边三角形,
∴AB=AC=BC,
∴DB=EC1,
∴四边形DECB的周长=129.
29.(1)小立方体中三面红的有8块,两面红的12块,一面红的6块,没有红色的1块.
(2)如果每面切三刀,小立方体中三面红的有8块,两面红的24块,一面红的24块,没有红色的8块.
(3)每面切n刀,小立方体中三面红的有8块,两面红的6(2n﹣2)块,一面红的6(n﹣1)2块,没有红色的(n﹣1)3块.
30.(1)两个圆锥形成的几何体;
(2)V圆锥πr2hπ×82×6=128π,
(3)①如图,解得r,
所以绕着斜边10所在的直线旋转一周形成的几何体的体积为V圆锥πr2hπ×()2×10=76.8π
②绕着直角边8所在的直线旋转一周形成的几何体的体积为V圆锥πr2hπ×62×8=96π,
故绕着直角边8所在的直线旋转一周形成的几何体的体积大.
一.选择题
1. “节日的焰火”可以说是( )
A.面与面交于线 B.点动成线
C.面动成体 D.线动成面
2. 将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A. B. C. D.
3. 如图,在下列图形中,绕铅垂线旋转一周可得到如图所示几何体的是( )
A. B. C. D.
4. 用一个平面去截正方体ABCD﹣A1B1C1D1(如图),所截得的截面不可能的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
5. 长方形纸板绕它的一条边旋转一周形成的几何体为( )
A.圆柱 B.棱柱 C.圆锥 D.球
6.如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是( )
A.长方体 B.球 C.圆柱 D.圆锥
7. 在下列几何体中,( )几何体是将一个三角尺绕它的斜边所在直线旋转一周得到的.
A. B. C. D.
8. 如图,在数学活动课上,同学们用一个平面分别去截下列四个几何体,所得截面是三角形的是( )
A. B.
C. D.
9. 如图,小明将装有一半水的密闭圆柱形玻璃杯水平放置,此时水面的形状为( )
A.圆 B.长方形 C.平行四边形 D.椭圆
10.一块长方体豆腐切三刀,最多能切成的块数(形状,大小不限)是( )
A.10 B.8 C.7 D.6
11.“笔尖在纸上快速滑动写出数字6”,运用数学知识解释这一现象( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交得线
12.下列语句中,不正确的是( )
A.图形平移是由移动的方向和距离所决定
B.图形旋转是由旋转中心和旋转角度所决定
C.中心对称图形是指一个图形绕其中的某一点旋转180°后能与其自身重合的图形
D.旋转后能重合的图形也是中心对称图形
13.如图是一个长方体截去两个角后的立体图形,如果照这样截去长方体的八个角,那么新的几何体的棱有( )
A.26条 B.30条 C.36条 D.42条
14.如图,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
二.填空题
15.一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的的体积是 立方厘米.(结果保留π)
16.将一根长4米的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60平方分米,这根木料的体积是 立方分米.
17.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说 .
18.用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;③可能是长方形;④可能是梯形.
其中正确结论的是 (填序号).
19.如图,一个5×5×5的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为 .
20.如图是一个三棱柱,用平面从中截去一个三棱柱后,剩下的几何体是 (写出所有可能的结果).
21.如图所示的几何体的截面形状分别是: .
22.已知一个直角三角形的两直角边分别是6cm,8cm.将这个直角三角形绕它的一直角边所在直线旋转一周,可以得到一个圆锥,则这个圆锥的体积是 cm3.(结果用π表示)
23.“齐天大圣”孙悟空有一个宝贝﹣﹣金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明 .
24.用一个平面去截长方体,截面 是正五边形(填“可能”或“不可能”).
三.解答题
25.一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
26.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为8cm、宽为4cm的长方形,统它的一条边所在的直线旋转一周,求得到的圆柱体的体积是多少?
27.第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.
图1旋转形成 ,图2旋转形成 ,图3旋转形成 ,
图4旋转形成 ,图5旋转形成 ,图6旋转形成 .
28.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形.如图,大正三棱柱的底面周长为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请直接写出四边形DECB的周长.
29.如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.问:
(1)小立方体中三面红的有几块?两面红的呢?一面红的呢?没有红色的面呢?
(2)如果每面切三刀,情况又怎样呢?
(3)每面切n刀呢?
30.在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体,V圆锥h)
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
答案
一.选择题
B.C.A.C.A.D.D.A.B.B.A.D.C.D.
二.填空题
15.12π或16π.
16.1200.
17.线动成面
18.①③④.
19.49.
20.三棱柱或四棱柱
21.长方形、圆、三角形
22.128π或96π.
23.线动成面
24.可能.
三.解答题
25.18.84÷3=6.28(分米),
6.28÷3.14÷2=1(分米),
3.14×12×3=9.42(立方分米);
3.14×12×2+18.84=25.12(平方分米).
答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
26.①绕长所在的直线旋转一周得到圆柱体积为:π×42×8=128π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×82×4=256π(cm3).
答:得到的圆柱体的体积是分别是128π(cm3)和256π(cm3)
27.图1旋转形成d,图2旋转形成a,图3旋转形成c,
图4旋转形成f,图5旋转形成b,图6旋转形成e.
28.(1)由题可得,截面的形状为长方形;
(2)∵△ADE是周长为3的等边三角形,
∴DE=AD=1,
又∵△ABC是周长为10的等边三角形,
∴AB=AC=BC,
∴DB=EC1,
∴四边形DECB的周长=129.
29.(1)小立方体中三面红的有8块,两面红的12块,一面红的6块,没有红色的1块.
(2)如果每面切三刀,小立方体中三面红的有8块,两面红的24块,一面红的24块,没有红色的8块.
(3)每面切n刀,小立方体中三面红的有8块,两面红的6(2n﹣2)块,一面红的6(n﹣1)2块,没有红色的(n﹣1)3块.
30.(1)两个圆锥形成的几何体;
(2)V圆锥πr2hπ×82×6=128π,
(3)①如图,解得r,
所以绕着斜边10所在的直线旋转一周形成的几何体的体积为V圆锥πr2hπ×()2×10=76.8π
②绕着直角边8所在的直线旋转一周形成的几何体的体积为V圆锥πr2hπ×62×8=96π,
故绕着直角边8所在的直线旋转一周形成的几何体的体积大.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
